i fly a lot. Conversas, reuniões, o que for. Normalmente prefiro um lugar no corredor, porque depois o tipo rude que cheira mal e espalha mais de 1,8 lugares só me irrita de um lado, e não estou encostado à janela.no entanto, às vezes gosto de agarrar um assento à janela, especialmente se estiver a voar perto do pôr-do-sol, ou sobre uma paisagem particularmente interessante (voar sobre o sul de Utah perto do pôr-do-sol irá mudar a sua vida)., Mas mesmo assim, a paisagem passa, e eventualmente você acaba voando sobre o leste do Colorado, e não há nada para ver além de terra plana, estendendo-se até o horizonte.e quando olho para as ondas âmbar de grãos até à linha que divide a terra e o céu, às vezes pergunto-me a que distância está essa linha. O horizonte é uma distância semi-mítica, usada na poesia como uma metáfora para uma divisão filosófica de algum tipo. Mas na verdade é uma coisa real, e a distância a ela pode ser determinada. Basta um pouco de Conhecimento da geometria e um diagrama para mostrar o caminho.,siga comigo. Vamos encontrar o Horizonte Perdido.então estás na Terra. Vamos assumir que a terra é uma esfera perfeita, porque Isso torna as coisas muito mais fáceis. Como é a nossa situação? Bem, parece algo como isto:
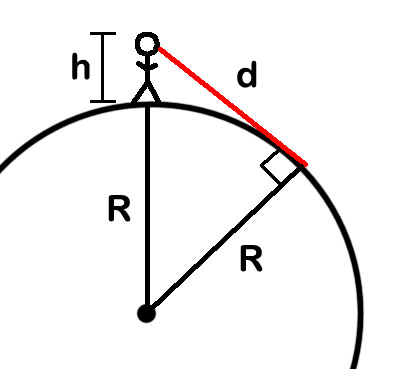
neste diagrama, o círculo é a superfície da Terra, que tem um raio de R. O raio da Terra varia com a latitude, mas só vou usar 6365 quilômetros como uma boa média., O cara que está na terra é um humano de altura h (não em escala, enorme duh lá). A linha de visão para o horizonte é a linha vermelha, chamada D. encontrar o valor de d é o objetivo aqui. Note que o raio da Terra é uma constante, mas que a dwill varia conforme o h sobe ou desce.
a chave aqui é que, no horizonte visível, o ângulo entre a sua linha de visão e a linha de raio da Terra é um ângulo direito (marcado no diagrama)., Isso significa que temos um triângulo, e alcançar de volta para o escuro, empoeirado de memória da escola — que significa que podemos usar o Teorema de Pitágoras para obter d. O quadrado da hipotenusa é igual à soma dos quadrados dos outros dois lados. De um lado é d, o outro é R e a hipotenusa é o raio da Terra, mais a sua altura acima da superfície, R+h. Isto dá-nos a seguinte fórmula algébrica:
d2 + R2 = (R+h)2
OK. E agora?, Bem, vamos expandir esse último termo usando FOLHA:
(R+h)2 = R2 + h2 + 2Rh
Suplente que volta para a primeira equação para obter
d2 + R2 = R2 + 2Rh + h2
Ei, temos um fator de R2 em ambos os lados, de modo que cancelar! Isso nos deixa com:
d2 = h2 + 2Rh
Agora, pegue a raiz quadrada de ambos os lados, e voilá! Você tem D.
então agora temos uma equação que nos diz quão longe o horizonte está dependendo de onde estamos acima da superfície. Podemos usar isso para colocar em valores diferentes para h, nossa altura, e ver quão longe está a borda da Terra., Coloquei isto numa planilha do Excel, e os números estão em baixo.
na tabela, a primeira coluna é a sua altura em metros acima da superfície da terra (na verdade a altura dos seus olhos) e a segunda coluna é a distância do horizonte em quilómetros. As colunas três e quatro são iguais, mas em pés e milhas para vocês, Amurcanos.verificação de sanidade: se estiver a 0 metros da superfície da Terra( deitado realmente plano), o horizonte fica a 0 quilómetros de distância. Faz sentido, estás tangente à superfície! Então a primeira linha soa bem.,agora imagine que está de pé numa praia, olhando para o mar até ao horizonte. A maioria das pessoas não tem dois metros de altura, e os seus olhos estão vários centímetros abaixo do topo da sua cabeça. Mas vamos apenas dizer que seus olhos estão a dois metros do chão (talvez você esteja em cima de uma duna de areia pequena). Nesse caso, o seu horizonte está a 5,1 km de distância. Isso também me soa bem.mas agora digamos que está no seu hotel com vista para a praia, e no chão os seus olhos estão a 20 metros do chão. O horizonte está então a 16 km de distância, muito mais longe do que antes., Bom: quanto mais alto você está, mais distante o horizonte deve estar.e se estiveres muito mais acima, como num avião? A uma altitude de cruzeiro de 39.000 pés (12.000 metros; típico para um voo de travessia do país) o horizonte está a 391 km (235 milhas) de distância! Isso é um caminho surpreendentemente longo; em geral isso significa que você pode estar olhando através de um ou mais estados nos EUA. Isto normalmente me engana; ver algo mesmo um pouco fora diretamente abaixo do avião significa que está a milhas de distância.e se subires ainda mais?, O ônibus espacial pode atingir uma altura máxima de cerca de 500 km (na verdade um pouco mais, mas perto o suficiente). São 500 mil metros, ou a segunda a última linha da mesa. Para eles, o horizonte está a quase 2600 km de distância! Isso significa que eles podem ver quase todos nós olhando de um lado do vaivém para o outro. Fresco.e se estiveres muito longe? A partir de uma distância infinita, você deve ver o horizonte como sendo um raio de terra mais distante do que a sua altura (desenhe um diagrama se quiser)., Na realidade isso é impossível, então na última linha eu coloquei nosso pobre observador flutuando no espaço a um milhão de quilômetros de distância (mais do dobro da distância à Lua). O horizonte está então a 1.006,344 km de distância, que é apenas cerca de (mas não completamente) o raio da terra mais a distância do observador sobre a superfície. Eles estão vendo quase — mas não completamente-metade da terra ao mesmo tempo.aqui está. Da próxima vez que estiveres numa praia, ou da próxima vez que estiveres a voar, olha para o horizonte. Como o fim de um arco-íris, é impossível de alcançar., Mas não é impossível — nem sequer é assim tão difícil-saber o quão longe está.Se gostou disto, veja as dez melhores maneiras de Mooey saber que a terra não é plana. Há ainda mais nerdidade geométrica lá.
Leave a Reply