vuelo mucho. Charlas, reuniones, lo que sea. Por lo general, prefiero un asiento del pasillo, porque entonces el tipo grosero que huele raro y se extiende sobre 1.8 asientos solo me irrita en un lado, y no estoy encajado contra la ventana.
sin embargo, a veces me gusta tomar un asiento en la ventana, especialmente si estoy volando cerca del atardecer, o sobre un paisaje particularmente interesante (volar sobre el sur de Utah cerca del atardecer cambiará tu vida)., Pero incluso entonces, el paisaje pasa volando, y eventualmente terminas volando sobre el Este de Colorado, y no hay nada que ver excepto tierra plana, plana, que se extiende hasta el horizonte.
y mientras miro por encima de las ondas ámbar de grano a la línea que divide la tierra y el cielo, a veces me pregunto cuán lejos está esa línea. El horizonte es una distancia semi-mítica, utilizada en la poesía como metáfora de una división filosófica de algún tipo. Pero de hecho es una cosa real, y la distancia a ella se puede determinar. Todo lo que se necesita es un poco de conocimiento de la geometría, y un diagrama para mostrar el camino.,
Sígueme aquí. Vamos a encontrar el horizonte perdido.
así que estás parado en la Tierra. Asumamos que la Tierra es una esfera perfecta, porque eso hace las cosas mucho más fáciles. ¿Cómo es nuestra situación? Bueno, se ve algo así:
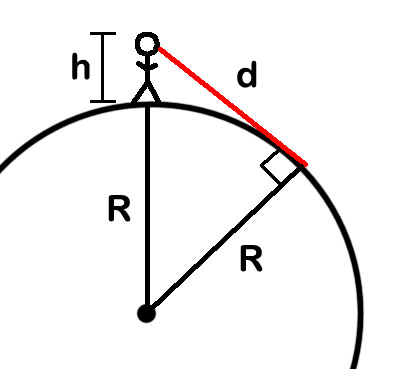
en este diagrama, el círculo es la superficie de la tierra, que tiene un radio de R. El radio de la Tierra varía con la latitud, pero solo usaré 6365 kilómetros como un promedio decente., El tipo de pie en la Tierra es un humano de altura h (NO a escala, enorme duh allí). La línea de visión hacia el horizonte es la línea roja, etiquetada d. Encontrar el valor de d es el objetivo aquí. Tenga en cuenta que el radio de la Tierra es una constante, pero que dwill variar a medida que h sube o baja.
la clave aquí es que en el horizonte visible, el ángulo entre su línea de visión y la línea del radio de la Tierra es un ángulo recto (marcado en el diagrama)., Eso significa que tenemos un triángulo rectángulo, y — llegar de nuevo en la memoria tenue, polvoriento de la escuela secundaria — que significa que podemos utilizar el Teorema de Pitágoras para obtener d. el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados. Un lado es d, el otro es R, y la hipotenusa es el radio de la Tierra más su altura sobre la superficie, R + h. esto nos da la siguiente fórmula algebraica:
d2 + R2 = (R+h)2
OK. ¿Y ahora qué?, Bueno, vamos a expandir ese último término usando FOIL:
(R + h) 2 = R2 + h2 + 2RH
sustituir que de nuevo en la primera ecuación para obtener
d2 + R2 = R2 + 2RH + h2
Hey, tenemos un factor de R2 en ambos lados, por lo que se cancelan! Eso nos deja con:
d2 = h2 + 2Rh
Ahora, toma la raíz cuadrada de ambos lados, y voila! Obtienes d.
así que ahora tenemos una ecuación que nos dice cuán lejos está el horizonte dependiendo de dónde estemos sobre la superficie. Podemos usar esto para poner diferentes valores para h, nuestra altura, y ver cuán lejos está el borde de la Tierra., Puse esto en una hoja de cálculo de Excel, y los números están abajo.
en la tabla, la primera columna es su altura en metros sobre la superficie de la tierra (realmente la altura de sus ojos) y la segunda columna es la distancia del horizonte en kilómetros. Las columnas tres y cuatro son las mismas, pero en pies y millas para ustedes los Amurcanos.
Control de Cordura: si estás a 0 metros de la superficie de la Tierra (acostado realmente, realmente plano), el horizonte está a 0 kilómetros de distancia. Eso tiene sentido-usted es tangente a la superficie! Así que la primera línea suena bien.,
Ahora imagine que está de pie en una playa, mirando hacia el océano hasta el horizonte. La mayoría de las personas no miden dos metros y tus ojos están varios centímetros por debajo de la parte superior de tu cabeza. Pero digamos que sus ojos están a dos metros del suelo (tal vez esté de pie en una pequeña duna de arena). En ese caso, su horizonte está a 5.1 km (3 millas) de distancia. Eso también me suena bien.
pero ahora digamos que estás en tu hotel con vistas a la playa, y en tu piso tus ojos están a 20 metros del suelo. El horizonte está entonces a 16 km, mucho más lejos que antes., Bueno: cuanto más alto estés, más lejos debería estar el horizonte.
¿Qué pasa si estás mucho más arriba, como en un avión? A una altitud de crucero de 39,000 pies (12,000 metros; típico para un vuelo a campo traviesa) el horizonte está a 391 km (235 millas) de distancia! Eso es un camino sorprendentemente largo; en general, eso significa que podría estar mirando a través de uno o más estados en los Estados Unidos. Esto comúnmente me engaña; ver algo incluso un poco fuera de directamente debajo del avión significa que está a millas de distancia.
¿Qué pasa si subes aún más alto?, El transbordador espacial puede alcanzar una altura máxima de unos 500 km (en realidad un poco más, pero lo suficientemente cerca). Son 500.000 metros, o la penúltima línea de la mesa. Para ellos, el horizonte está a casi 2600 km de distancia! Eso significa que pueden ver casi todo nosotros mirando de un lado del transbordador al otro. Fresco.
¿y si estás realmente lejos? Desde una distancia infinita, deberías ver el horizonte como un radio terrestre más lejos que tu altura (dibuja un diagrama si quieres)., En realidad eso es imposible, así que en la última línea puse a nuestro pobre observador flotando en el espacio a un millón de kilómetros de distancia (más del doble de la distancia a la Luna). El horizonte está entonces a 1.006.344 km de distancia, que es casi (pero no del todo) el radio de la Tierra más la distancia del observador sobre la superficie. Están viendo casi — pero no del todo-la mitad de la Tierra a la vez.
así que ahí lo tienes. La próxima vez que estés en una playa, o la próxima vez que estés volando, mira hacia el horizonte. Como el final de un arco iris, es imposible de alcanzar., Pero no es imposible — ni siquiera es tan difícil — saber cuán lejos está.
si te gustó esto, echa un vistazo a las diez mejores maneras de mooey de saber que la Tierra no es plana. Hay aún más Nerd geométrico allí.
Leave a Reply