Jag flyger mycket. Samtal, möten, vad som helst. Jag brukar föredra en gångplats, för då irriterar den oförskämda killen som luktar roligt och sprider sig över 1,8 platser mig bara på ena sidan, och jag är inte fastklämd mot fönstret.
men ibland gillar jag att ta ett fönstersäte, speciellt om jag flyger nära solnedgången, eller över ett särskilt intressant landskap (flyger över södra Utah nära solnedgången kommer att förändra ditt liv)., Men även då, landskapet blåser förbi, och så småningom du hamnar flyger över östra Colorado, och det finns inget att se men platt, platt mark, sträcker sig hela vägen till horisonten.
och när jag tittar över de gula vågorna av korn till linjen som delar Mark och himmel, undrar jag ibland hur långt bort den linjen är. Horisonten är ett halvmytiskt avstånd, som används i poesi som en metafor för en filosofisk uppdelning av något slag. Men i själva verket är det en riktig sak, och avståndet till det kan bestämmas. Allt som krävs är lite kunskap om geometri, och ett diagram för att visa dig vägen.,
Följ med mig här. Vi ska hitta den förlorade horisonten.
så du står på jorden. Låt oss anta att jorden är en perfekt sfär, för det gör det mycket lättare. Hur ser vår situation ut? Tja, det ser ut så här:
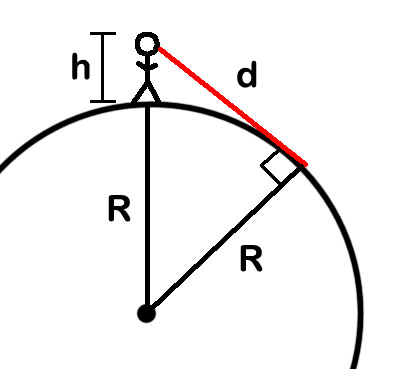
i det här diagrammet är cirkeln jordens yta, som har en radie av R. jordens radie varierar med latitud, men jag använder bara 6365 kilometer som ett anständigt genomsnitt., Killen som står på jorden är en människa av höjd h (inte skala, stor duh där). Siktlinjen till horisonten är den röda linjen, märkt d.att hitta värdet av d är målet här. Observera att jordens radie är en konstant, men att dwill varierar när h går upp eller ner.
det viktigaste här är att vid den synliga horisonten är vinkeln mellan din synlinje och jordens radielinje en rät vinkel (markerad i diagrammet)., Det betyder att vi har en rätt triangel, och — nå tillbaka till det svaga, dammiga minnet på gymnasiet — det betyder att vi kan använda Pythagoras sats för att få d.hypotenusans kvadrat är lika med summan av kvadraterna på de andra två sidorna. Ena sidan är d, den andra är R, och hypotenusen är jordens radie plus din höjd över ytan, R + h. Detta ger oss följande algebraiska formel:
D2 + R2 = (R+h)2
OK. Vad gör vi nu?, Tja, låt oss expandera den sista termen med folie:
(R+h)2 = R2 + H2 + 2RH
ersätt den tillbaka till den första ekvationen för att få
D2 + R2 = R2 + 2RH + h2
Hej, Vi har en faktor R2 på båda sidor, så de avbryter! Det lämnar oss med:
D2 = H2 + 2RH
nu, ta kvadratroten på båda sidor och voila! Du får d.
så nu har vi en ekvation som berättar hur långt bort horisonten är beroende på var vi är över ytan. Vi kan använda detta för att sätta i olika värden för H, vår höjd, och se hur långt bort kanten av jorden är., Jag lägger detta i ett Excel-kalkylblad, och siffrorna är nedan.
i tabellen är den första kolumnen din höjd i meter över jordens yta (verkligen höjden på dina ögon) och den andra kolumnen är horisontavståndet i kilometer. Kolumnerna tre och fyra är desamma, men i fötter och miles för dig Amurcans.
Sanity check: om du är 0 meter från jordens yta (ligger verkligen riktigt platt) är horisonten 0 kilometer bort. Det är vettigt-du är tangent till ytan! Så den första raden låter rätt.,
föreställ dig nu att du står på en strand och ser ut över havet till horisonten. De flesta människor är inte två meter höga, och dina ögon är flera centimeter under toppen av ditt huvud. Men låt oss bara säga att dina ögon är två meter från marken (kanske står du på en liten sanddyn). I så fall är din horisont 5,1 km bort. Det låter också rätt för mig.
men låt oss nu säga att du är på ditt hotell med utsikt över stranden, och på ditt golv är dina ögon 20 meter från marken. Horisonten är då 16 km bort, mycket längre än tidigare., Bra: ju högre du är, desto längre bort bör horisonten vara.
vad händer om du är mycket högre upp, som i ett flygplan? Vid en marschhöjd på 39,000 fot (12,000 meter; typiskt för en längdåkning flygning) horisonten är 391 km (235 miles) bort! Det är en förvånansvärt lång väg; i allmänhet betyder det att du kan titta över en eller flera stater i USA. Detta ofta dårar mig; att se något även lite ut från direkt under Planet innebär att det är miles away.
vad händer om du går upp ännu högre?, Rymdfärjan kan nå en maximal höjd på ca 500 km (faktiskt lite mer, men tillräckligt nära). Det är 500 000 meter, eller den näst sista raden i tabellen. För dem är horisonten nästan 2600 km bort! Det betyder att de kan se nästan hela USA genom att titta från ena sidan av skytteln till den andra. Cool.
och vad händer om du är riktigt långt borta? Från ett oändligt avstånd bör du se horisonten som en Jordradie längre bort än din höjd (rita ett diagram om du vill)., I verkligheten är det omöjligt, så i sista raden satte jag vår stackars observatör flytande i rymden en miljon kilometer bort (mer än dubbelt så långt som månen). Horisonten är sedan 1,006,344 km bort, vilket är ungefär (men inte riktigt) jordens radie plus observatörens avstånd över ytan. De ser nästan — men inte riktigt — halva jorden på en gång.
så där går du. Nästa gång du är på en strand, eller nästa gång du flyger, ta en titt ut mot horisonten. Liksom slutet på en regnbåge är det omöjligt att nå., Men det är inte omöjligt — det är inte ens så svårt-att veta hur långt bort det är.
om du gillade det här, ta en titt på Mooeys topp tio sätt att veta att jorden inte är platt. Det finns ännu mer geometrisk nerdity där.
Leave a Reply