użyj poniższych kalkulatorów, aby obliczyć powierzchnię kilku popularnych kształtów., Surface Area
Cone Surface Area
Cube Surface Area
Cylindrical Tank Surface Area
Rectangular Tank Surface Area
Capsule Surface Area
Cap Surface Area
Please provide any two values below to calculate.,
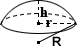
Powierzchnia stożkowa Frustum
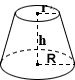
Powierzchnia elipsoidalna
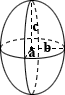
kwadratowa Powierzchnia piramidy
powiązany kalkulator objętości/Kalkulator powierzchni ciała/Kalkulator powierzchni ciała
powierzchnia ciała stałego jest miarą całkowitej powierzchni zajmowanej przez powierzchnię obiektu., Wszystkie obiekty adresowane w tym kalkulatorze są opisane bardziej szczegółowo na stronach Kalkulator objętości i kalkulator powierzchni. Jako takie, ten kalkulator skupi się na równaniach do obliczania powierzchni obiektów i wykorzystania tych równań. Więcej szczegółów na temat poszczególnych obiektów można znaleźć w powyższych kalkulatorach.
Sfera
pole powierzchni (SA) kuli można obliczyć za pomocą równania:
SA = 4NR2
Gdzie r to promień
Xael nie lubi dzielić się z nikim czekoladowymi truflami., Kiedy otrzymuje pudełko trufli Lindt, przystępuje do obliczenia powierzchni każdej trufli, aby określić całkowitą powierzchnię, którą musi Lizać, aby zmniejszyć prawdopodobieństwo, że ktoś spróbuje zjeść jej trufle. Biorąc pod uwagę, że każda trufla ma promień 0,325 cala:
SA = 4 × π × 0,3252 = 1,327 in2
Stożek
powierzchnię stożka okrągłego można obliczyć sumując powierzchnię każdego z jego poszczególnych składników., „Podstawa SA” odnosi się do okręgu, który zawiera podstawę w zamkniętym stożku okrągłym, podczas gdy boczne SA odnosi się do reszty obszaru stożka między podstawą a jego wierzchołkiem., Równania do obliczenia każdego z nich, a także całkowita SA zamkniętego okrągłego stożka są przedstawione poniżej:
base SA = nr2
lateral SA = nr√r2 + h2
total SA = nr(r + √R2 + h2)
Gdzie R to promień, A h to wysokość
Athena ostatnio zainteresowała się kulturą Azji Południowo-Wschodniej i jest szczególnie zafascynowana stożkowym kapeluszem, Zwykle określanym jako „kapelusz ryżowy”, który jest powszechnie stosowany w wielu krajach Azji Południowo-Wschodniej., Postanawia zrobić sobie własną, a będąc osobą bardzo praktyczną, nie pogrążoną w sentymentalizmie, ściąga suknię ślubną matki z ciemnych zakamarków szafy, w której się znajduje. Określa ona powierzchnię materiału potrzebnego do stworzenia kapelusza o promieniu 1 stopy i wysokości 0,5 stopy w następujący sposób:
boczna SA = π × 0,4√0,42 + 0,52 = 0.,805 m2
sześcian
powierzchnię sześcianu można obliczyć sumując całkowite obszary jego sześciu kwadratowych powierzchni:
SA = 6A2
Gdzie a to długość krawędzi
Anne chce dać młodszemu bratu kostkę Rubika na urodziny, ale wie, że jej brat ma krótki czas uwagi i jest łatwo sfrustrowany. Na zamówienie zamawia Kostkę Rubika, w której wszystkie twarze są Czarne i musi zapłacić za dostosowanie w oparciu o powierzchnię sześcianu o długości krawędzi 4 cale.,
SA = 6 × 42 = 96 in2
zbiornik Cylindryczny
pole powierzchni zamkniętego cylindra można obliczyć sumując całkowite obszary jego podstawy i powierzchni bocznej:
base SA = 2NR2
lateral SA = 2NRH
total SA = 2NR(r + h), gdzie R to promień, A h to wysokość
Jeremy ma duży Cylindryczny zbiornik, w którym kąpie się, ponieważ nie lubi pryszniców ani wanien. Jest ciekaw, czy jego podgrzewana woda chłodzi się szybciej niż w wannie i musi obliczyć powierzchnię cylindrycznego zbiornika o wysokości 5,5 stopy i promieniu 3,5 stopy.
razem SA = 2 × 3.,
Powierzchnia prostokątnego zbiornika jest sumą powierzchni każdej z jego twarzy:
SA = 2LW + 2LH + 2WH
Gdzie L to długość, w to szerokość, a h to wysokość
Banana, najstarsza córka długiej linii plantatorów bananów, chce nauczyć swoją zepsutą, zgniłą siostrę, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, chleb bananowy, Lekcja o nadziei i oczekiwaniach. Banana-Bread cały tydzień krzyczała, że chce nowego zestawu szuflad do domu jej nowe figurki Batmana., W związku z tym Banan kupuje jej duży domek dla lalek Barbie z limitowaną edycją naczyń kuchennych, piekarnika, fartucha i realistycznych gnijących bananów dla Batmana., Pakuje je do prostokątnego pudełka o podobnych wymiarach, jak szuflada, której chce. musi określić ilość papieru do pakowania, której potrzebuje, aby zakończyć prezentację prezentu z niespodzianką 3 ft × 4 ft × 5 Ft:
SA = (2 × 3 × 4) + (2 × 4 × 5) + (2 × 3 × 5) = 94 ft2
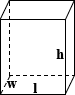
kapsuła
powierzchnia kapsuły może być określona przez połączenie równań powierzchni kuli i powierzchni bocznej cylindra., Należy zauważyć, że powierzchnia podstaw cylindra nie jest uwzględniona, ponieważ nie obejmuje ona części powierzchni kapsuły. Całkowita powierzchnia jest obliczana w następujący sposób:
SA = 4NR2 + 2NRH
Gdzie r to promień, A h to wysokość
Horatio produkuje placebo, które ma na celu doskonalenie indywidualności, krytycznego myślenia i zdolności do obiektywnego i logicznego podejścia do różnych sytuacji., Już przetestował rynek i odkrył, że zdecydowana większość populacji nie wykazuje żadnej z tych cech i jest bardzo gotowa do zakupu swojego produktu, jeszcze bardziej zakorzeniając się w cechach, z których tak desperacko starają się uciec. Horatio musi określić powierzchnię każdej kapsułki, aby mógł pokryć je nadmierną warstwą cukru i odwołać się do predysponowanych do cukru języków populacji w ramach przygotowań do następnego placebo, które „leczy” wszystkie formy cukrzycy. Biorąc pod uwagę, że każda kapsułka ma r 0,05 cala i h 0,5 cala:
SA = 4π × 0.,052 + 2π × 0.05 × 0.5 = 0.188 in2
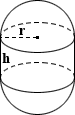
nasadka sferyczna
powierzchnia nasadki sferycznej zależy od wysokości danego segmentu. Dostarczony Kalkulator zakłada stałą kulę i uwzględnia podstawę pokrywy w obliczeniach powierzchni, gdzie całkowita powierzchnia jest sumą powierzchni podstawy i powierzchni bocznej pokrywy sferycznej. Jeśli za pomocą tego kalkulatora obliczyć pole powierzchni pustej kuli, odjąć pole powierzchni podstawy., Biorąc pod uwagę dwie wartości wysokości, promienia nasadki lub promienia podstawy, trzecią wartość można obliczyć za pomocą równań podanych w kalkulatorze objętości. Równania powierzchni są następujące:
Czapka sferyczna SA = 2nrh
baza sa = nr2
całkowita kula sferyczna SA = 2nrh + nr2
Gdzie R to promień czapki sferycznej, R to promień podstawy, a h to wysokość
Jennifer jest zazdrosna o Globus, który jej starszy brat Lawrence otrzymał na urodziny. Ponieważ Jennifer ma 2/3 wieku swojego brata, postanawia, że zasługuje na 1/3 globu swojego brata., Po zwróceniu piły ojca do szopy z narzędziami, oblicza powierzchnię swojej pustej części kuli ziemskiej z R 0,80 stopy i h 0,53 stopy, jak pokazano poniżej:
SA = 2π × 0,80 × 0,53 = 2.,664 m2
Frustum stożkowe
powierzchnia bryły, prawej stożkowej frustum jest sumą obszarów jej dwóch okrągłych końców i jego bocznej powierzchni:
okrągły koniec SA = π(R2 + r2)
boczny SA = π(r+r)√(r-r)2 + h2
razem SA = π(R2 + R2) + π(r+r)√(r-r)2 + H2
gdzie R i R to promienie końców, H to wysokość
Paul na potrzeby swojego projektu Science Fair tworzy wulkan w kształcie stożka., Paul postrzega erupcje wulkanów jako zjawisko gwałtowne, a będąc przeciwnikiem wszelkich form przemocy, postanawia uczynić swój wulkan w formie zamkniętej stożkowej frustum, która nie wybucha. Chociaż jego wulkan jest mało prawdopodobne, aby zaimponować sędziom science fair, Paul musi nadal określić powierzchnię materiału, którego potrzebuje, aby pokryć zewnętrzną ścianę swojego wulkanu R 1 stopy, r 0,3 stopy i h 1,5 stopy:
razem SA = π (12 + 0,32) + π(1 + 0.3) √(1 – 0.3)2 + 1.52 = 10.,185 m2
Elipsoida
obliczanie powierzchni elipsoidy nie ma prostego, dokładnego wzoru, takiego jak sześcian lub inny prostszy kształt. Powyższy kalkulator używa przybliżonego wzoru, który zakłada prawie sferyczną elipsoidę:
SA ≈ 4π 1.6√(a1.6B1.6 + A1.6C1.6 + b1.6C1.6)/3
Gdzie A, b I c są osiami elipsy
Coltaine zawsze lubił gotowanie i niedawno wygrał ceramiczny nóż z konkursu. Niestety dla jego rodziny, która prawie wyłącznie je mięso, Coltaine ćwiczył swoją technikę krojenia na nadmiernej ilości warzyw., Zamiast jeść warzywa, ojciec Coltaine patrzy przygnębiająco na jego talerz i szacuje powierzchnię eliptycznych cięć cukinii z osiami 0,1, 0,2 i 0,35 cala:
SA ≈ 4π 1.6√(0.11.60.21.6 + 0.11.60.351.6 + 0.21.60.351.6)/3 = 0.562 in2
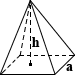
kwadratowa Piramida
powierzchnia kwadratowej piramidy składa się z obszaru jej kwadratowej podstawy i obszaru każdej z jej czterech trójkątnych twarzy., Biorąc pod uwagę wysokość h i długość krawędzi a, Pole powierzchni można obliczyć za pomocą następujących równań:
base SA = a2
lateral sa = 2a√(a/2)2 + h2
total SA = A2 + 2a√(a/2)2 + h2
Klasa Vonquayli niedawno zakończyła budowę modelu Wielkiej Piramidy w Gizie. Uważa jednak, że model nie emanuje uczuciem architektonicznego cudu, które robi Oryginał i decyduje, że pokrycie go „śniegiem” nada przynajmniej aspekt cudu., Oblicza powierzchnię stopionego cukru, która musiałaby w pełni pokryć piramidę o długości krawędzi a 3 stóp i wysokości h 5 stóp:
razem SA = 32 + 2 × 3√(3/2)2 + 52 = 40.321 ft2
w przeciwieństwie do Wielkiej Piramidy w Gizie, która stoi od tysięcy lat, jej model, wykonany z krakersów grahamskich i pokryty cukrem, trwał tylko kilka dni.
jednostki obszaru wspólnego
| Jednostka | meter2 |
| kilometr2 | 1 000 000 |
| centymetr2 | 0.0001 |
| milimetr2 | 0.,000001 |
| micrometer2 | 0.000000000001 |
| hectare | 10,000 |
| mile2 | 2,589,990 |
| yard2 | 0.83613 |
| foot2 | 0.092903 |
| inch2 | 0.00064516 |
| acre | 4,046.86 |
Leave a Reply