Ik vlieg veel. Gesprekken, vergaderingen, wat dan ook. Ik heb meestal liever een gangpad stoel, omdat dan de onbeschofte man die ruikt raar en spreidt over 1.8 stoelen alleen irriteert me aan de ene kant, en ik ben niet klem tegen het raam.
echter, soms grijp ik graag een stoel bij het raam, vooral als ik vlieg in de buurt van zonsondergang, of over een bijzonder interessant landschap (vliegen over Zuid-Utah in de buurt van zonsondergang zal je leven veranderen)., Maar zelfs dan waait het landschap voorbij, en uiteindelijk vlieg je over Oost Colorado, en er is niets anders te zien dan plat, plat land, helemaal tot aan de horizon.
en als ik over de amber golven van graan kijk naar de lijn die land en hemel verdeelt, vraag ik me soms af hoe ver die lijn is. De horizon is een semi-mythische afstand, gebruikt in poëzie als metafoor voor een filosofische verdeling van een soort. Maar in feite is het een echt ding, en de afstand tot het kan worden bepaald. Het enige wat je nodig hebt is een beetje kennis van geometrie, en een diagram om je de weg te wijzen.,
Volg hier met mij mee. We gaan de verloren horizon vinden.
dus je staat op de aarde. Laten we aannemen dat de aarde een perfecte bol is, want dat maakt het een stuk makkelijker. Hoe ziet onze situatie eruit? Nou, het ziet er ongeveer zo uit:
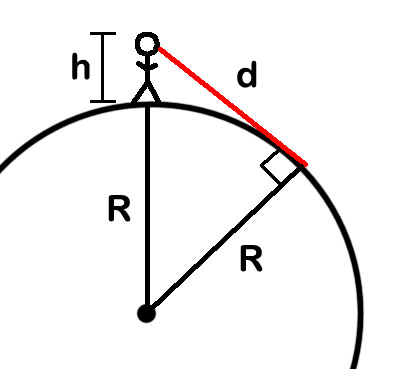
in dit diagram is de cirkel het oppervlak van de aarde, die een straal van R. de straal van de aarde varieert met de breedtegraad, maar ik gebruik 6365 kilometer als een fatsoenlijk gemiddelde., De dude die op de Aarde staat is een mens van de hoogte h (niet op schaal, enorme duh daar). De zichtlijn naar de horizon is de rode lijn, gelabeld d. het vinden van de waarde van d is hier het doel. Merk op dat de straal van de aarde een constante is, maar dat dwill variëren als h omhoog of omlaag gaat.
het belangrijkste is dat aan de zichtbare horizon de hoek tussen je zichtlijn en de straallijn van de aarde een rechte hoek is (aangegeven in het diagram)., Dat betekent dat we een rechthoekige driehoek hebben, en-reik terug in de vage, stoffige herinnering van de middelbare school — dat betekent dat we de Stelling van Pythagoras kunnen gebruiken om d te krijgen. het kwadraat van de hypotenusa is gelijk aan de som van de kwadraten van de andere twee zijden. De ene kant is d, de andere is R, en de hypotenusa is de straal van de aarde plus uw hoogte boven het oppervlak, R + h. dit geeft ons de volgende algebraïsche formule:
d2 + R2 = (R+h)2
OK. Wat nu?, Nou, laten we die laatste term uitbreiden met behulp van folie:
(R+h)2 = R2 + h2 + 2Rh
Vervang dat terug in de eerste vergelijking om
D2 + R2 = R2 + 2Rh + h2
Hey, we hebben een factor R2 aan beide zijden, dus ze annuleren! Dat laat ons met:
d2 = h2 + 2Rh
neem nu de vierkantswortel van beide zijden, en voila! Je krijgt d.
dus nu hebben we een vergelijking die ons vertelt hoe ver weg de horizon is, afhankelijk van waar we boven het oppervlak zijn. We kunnen dit gebruiken om verschillende waarden in te voeren voor h, onze hoogte, en te zien hoe ver weg de rand van de aarde is., Ik zet dit in een Excel-spreadsheet, en de nummers zijn hieronder.
in de tabel is de eerste kolom je hoogte in meters boven het aardoppervlak (eigenlijk de hoogte van je ogen) en de tweede kolom is de horizonafstand in kilometers. Kolommen drie en vier zijn hetzelfde, maar in voet en mijlen voor jullie Amurcans.
Saniteitscontrole: als je 0 meter van het aardoppervlak bent (liggend heel plat), is de horizon 0 kilometer verderop. Dat is logisch — je bent raaklijn aan de oppervlakte! Dus de eerste regel klinkt goed.,
stel je nu voor dat je op een strand staat, uitkijkend over de oceaan naar de horizon. De meeste mensen zijn niet twee meter lang, en je ogen zijn enkele centimeters onder de bovenkant van je hoofd. Maar laten we zeggen dat je ogen twee meter van de grond staan (misschien sta je op een klein zandduin). In dat geval ligt uw horizon 5,1 km verderop. Dat klinkt ook goed voor mij.
maar laten we nu zeggen dat u in uw hotel met uitzicht op het strand, en op uw vloer uw ogen zijn 20 meter van de grond. De horizon is dan 16 km verderop, veel verder dan voorheen., Goed: hoe hoger je bent, hoe verder de horizon zou moeten zijn.
Wat als je een stuk hoger staat, zoals in een vliegtuig? Op een kruishoogte van 12.000 meter (typisch voor een langlaufvlucht) ligt de horizon op 391 km afstand! Dat is een verrassend lange weg; in het algemeen betekent dat dat je zou kunnen kijken over een of meer staten in de VS. Dit Houdt me vaak voor de gek; iets zien zelfs een beetje uit direct onder het vliegtuig betekent dat het mijlen ver weg.
Wat als u nog hoger gaat?, De spaceshuttle kan een maximale hoogte bereiken van ongeveer 500 km (eigenlijk iets meer, maar dichtbij genoeg). Dat is 500.000 meter, of de op één na laatste regel van de tafel. Voor hen ligt de horizon op bijna 2600 km afstand! Dat betekent dat ze ons bijna helemaal kunnen zien door van de ene kant van de Shuttle naar de andere te kijken. Koel.
en wat als je echt ver weg bent? Vanuit een oneindige afstand zou je de horizon moeten zien als één straal van de Aarde verder weg dan je hoogte (teken een diagram als je wilt)., In werkelijkheid is dat onmogelijk, dus zet ik in de laatste regel onze arme waarnemer een miljoen kilometer verder in de ruimte (meer dan twee keer de afstand tot de maan). De horizon is dan 1.006.344 km verwijderd, wat ongeveer (maar niet helemaal) de straal van de aarde plus de afstand van de waarnemer over het oppervlak is. Ze zien bijna — maar niet helemaal — de helft van de aarde in één keer.
dus daar ga je. De volgende keer dat je op het strand bent, of de volgende keer dat je vliegt, kijk dan naar de horizon. Net als het einde van een Regenboog, is het onmogelijk te bereiken., Maar het is niet onmogelijk — het is niet eens zo moeilijk-om te weten hoe ver het is.
als je dit leuk vindt, kijk dan eens naar Mooey ‘ s Top Tien manieren om te weten dat de aarde niet plat is. Er is nog meer geometrische nerditeit daar.
Leave a Reply