lennän paljon. Puheita, kokouksia, mitä vain. Yleensä pidän enemmän käytäväpaikasta, sillä silloin epäkohtelias kaveri, joka haisee hassulta ja levittäytyy 1,8-paikkaiseksi, ärsyttää vain toisella puolella, enkä ole kiilautunut ikkunaa vasten.
kuitenkin joskus tykkään tarttua ikkunapaikalle, varsinkin jos lennän lähellä auringonlaskua tai erityisen kiinnostavan maiseman yllä (lentäminen Etelä-Utahin yllä lähellä auringonlaskua muuttaa elämäsi)., Mutta silloinkin, maisema puhaltaa ohi, ja lopulta päädyt lentävät yli itä-Colorado, ja siellä ei ole mitään nähdä, mutta tasainen, tasainen maa, joka ulottuu koko matkan horisonttiin.
ja kun katselen viljan meripihkan aaltojen yli maata ja taivasta jakavaan linjaan, mietin joskus, kuinka kaukana se raja on. Horisontti on puoliksi myyttinen etäisyys, jota käytetään runoudessa jonkinlaisen filosofisen jaon metaforana. Mutta itse asiassa se on todellinen asia, ja etäisyys siihen voidaan määrittää. Tarvitaan vain vähän tietoa geometriasta ja kaavio, joka näyttää tien.,
Follow along with me here. Löydämme kadonneen horisontin.
so you ’ re standing on the Earth. Oletetaan, että maa on täydellinen pallo, koska se helpottaa asioita. Miltä tilanteemme näyttää? No, se näyttää tältä:
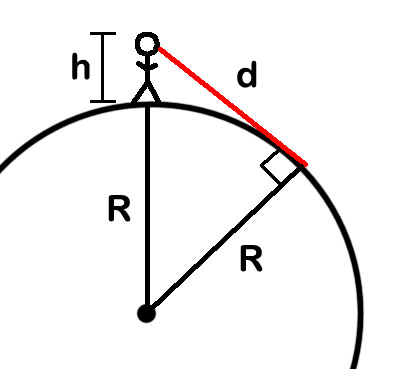
tässä kaavio, ympyrä on Maan pinnalla, joka on etäisyydellä R Maapallon säde vaihtelee leveysasteen, mutta käytän 6365 km kuten kunnon keskiarvo., Maan päällä seisova jätkä on ihminen, jonka korkeus on H (ei mittakaava, valtava duh siellä). Näköyhteys horisonttiin on punainen viiva, jossa lukee d.D: n arvon löytäminen on tässä tavoitteena. Huomaa, että säde maan on vakio, mutta että dwill vaihtelevat kuin h menee ylös tai alas.
keskeinen asia tässä on, että näkyvissä horisontin välinen kulma linja-of-sight ja säde line Maa on oikeassa kulmassa (merkitty kuvassa)., Se tarkoittaa, että meillä on oikea kolmio, ja — saavuttaa takaisin hämärään, pölyinen muistiin lukio — että tarkoittaa, että voimme käyttää Pythagoraan lausetta päästä d. Neliön hypotenuusa on yhtä suuri summa neliöiden kaksi muuta sivua. Toinen puoli on d, toinen on R, ja hypotenuusa on Maapallon säde plus korkeus pinnan yläpuolella, R+s. Tämä antaa meille seuraavat algebrallinen kaava:
d2 + R2 = (R+h)2
OK. Mitä nyt?, No, katsotaanpa laajentaa, että viimeinen termi käyttäen FOLIO:
(R+h)2 = R2 + h2 + 2Rh
Korvike, että takaisin ensimmäinen yhtälö saada
d2 + R2 = R2 + 2Rh + h2
– meillä on tekijä R2: n molemmin puolin, joten ne kumoavat! Se jättää meille:
d2 = h2 + 2Rh
Nyt, ota neliöjuuri molemmilta puolilta, ja voila! Saat d.
Joten nyt meillä on yhtälö, joka kertoo, kuinka kaukana horisontti on riippuen siitä, missä olemme pinnan yläpuolella. Voimme käyttää tätä asettaaksemme erilaisia arvoja h: lle, korkeudellemme ja nähdäksemme, kuinka kaukana maan reuna on., Laitoin tämän Excel-taulukkolaskentaan, ja numerot ovat alla.
taulukon ensimmäisessä sarakkeessa on korkeutta in metrin korkeudella Maan pinnasta (oikeasti korkeus silmäsi) ja toisessa sarakkeessa on horisontin etäisyys kilometreinä. Pylväät kolme ja neljä ovat samat, mutta jalat ja mailia teille Amurcans.
Järki tarkistaa: jos olet 0 metriä Maan pinnan (makuulla todella tasainen), horisontti on 0 kilometrin päässä. Siinä on järkeä-olet tangentti pinnalle! Ensimmäinen rivi kuulostaa siis oikealta.,
nyt kuvitelkaa, että seisotte rannalla katsellen meren yli horisonttiin. Useimmat ihmiset eivät ole kaksi metriä pitkiä, ja silmäsi ovat useita senttejä pään yläosan alapuolella. Mutta sanotaan vain, että silmäsi ovat kahden metrin päässä Maasta (ehkä seisot pienellä hiekkadyynillä). Silloin horisonttisi on 5,1 kilometrin päässä. Sekin kuulostaa minusta oikealta.
mutta nyt sanotaan, että olet hotellissasi näkymät rannalle, ja lattialla silmäsi ovat 20 metrin päässä Maasta. Horisontti on silloin 16 kilometrin päässä, paljon kauempana kuin ennen., Hyvä: mitä korkeampi olet, sitä kauempana horisontin pitäisi olla.
entä jos on paljon korkeammalla, kuten lentokoneessa? Cruising altitude 39000 jalkaa (12000 metriä; tyypillinen matkalento) horisontti on 391 km (235 km) päässä! Se on yllättävän pitkä matka; yleensä se tarkoittaa, että voit olla etsivät koko yhden tai useamman valtion yhdysvalloissa. Tämä yleensä hämää minua; kun näen jotain edes vähän suoraan koneen alta, se on kilometrien päässä.
entä jos nouset vielä korkeammalle?, Avaruussukkula voi saavuttaa maksimikorkeuden noin 500 km (itse asiassa hieman enemmän, mutta riittävän lähellä). Se on 500 000 metriä eli pöydän toiseksi viimeinen rivi. Heille horisontti on lähes 2600 km: n päässä! Se tarkoittaa, että he näkevät lähes koko USA: n katsomalla sukkulan toiselta puolelta toiselle. Jäähtyä.
ja mitä jos olet todella kaukana? Äärettömältä etäisyydeltä katsottuna horisontin pitäisi olla yhden maan säde kauempana korkeudestasi (piirrä kaavio, jos haluat)., Todellisuudessa se on mahdotonta, joten viimeisellä rivillä laitoin köyhän tarkkailijamme kellumaan avaruudessa miljoonan kilometrin päähän (yli kaksi kertaa etäisyys Kuuhun). Horisontti on sitten 1,006,344 km: n päässä, joka on vain noin (mutta ei aivan) Maapallon säde plus tarkkailijan etäisyys pinnan yli. He näkevät lähes — mutta eivät aivan-puolet maasta kerralla.
so there you go. Seuraavan kerran kun olet rannalla tai seuraavan kerran lennät, katso horisonttiin. Kuten sateenkaaren päässä, sitä on mahdoton saavuttaa., Mutta se ei ole mahdotonta — se ei ole edes niin vaikeaa — tietää, kuinka kaukana se on.
Jos pidit tästä, katsohan Mooey Kymmenen tapaa tietää, että Maapallo ei ole litteä. Siellä on vielä geometrisempaa nörttimäisyyttä.
Leave a Reply