Oberflächenrechner

Verwenden Sie die folgenden Rechner, um die Oberfläche mehrerer gebräuchlicher Formen zu berechnen., Surface Area

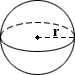
Cone Surface Area

Cube Surface Area

Cylindrical Tank Surface Area

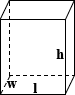
Rectangular Tank Surface Area

Capsule Surface Area

Cap Surface Area

Please provide any two values below to calculate.,

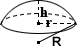
Konische Frustumoberfläche

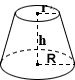
Ellipsoide Oberfläche

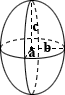
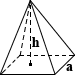
Quadratische Pyramidenoberfläche

Related Volume Calculator | Area Calculator | Body Surface Area Calculator

Die Oberfläche eines Festkörpers ist ein Maß für die Gesamtfläche, die von der Oberfläche eines Objekts eingenommen wird., Alle in diesem Rechner angesprochenen Objekte werden auf den Seiten Volumenrechner und Flächenrechner ausführlicher beschrieben. Daher konzentriert sich dieser Rechner auf die Gleichungen zur Berechnung der Oberfläche der Objekte und die Verwendung dieser Gleichungen. Bitte beachten Sie die oben genannten Rechner für weitere Details zu jedem einzelnen Objekt.

Kugel

Die Oberfläche (SA) einer Kugel kann mit der Gleichung berechnet werden:

SA = 4nr2
wobei r der Radius ist

Xael mag es nicht, ihre Schokoladentrüffel mit jemandem zu teilen., Wenn sie eine Schachtel Lindt-Trüffel erhält, berechnet sie die Oberfläche jedes Trüffels, um die gesamte Oberfläche zu bestimmen, die sie lecken muss, um die Wahrscheinlichkeit zu verringern, dass jemand versucht, ihre Trüffel zu essen. Angesichts der Tatsache, dass jeder Trüffel einen Radius von 0,325 Zoll hat:

SA = 4 × π × 0,3252 = 1,327 in2

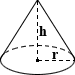
Kegel

Die Oberfläche eines Kreiskegels kann berechnet werden, indem die Oberfläche jeder seiner einzelnen Komponenten summiert wird., Die „Basis SA“ bezieht sich auf den Kreis, der die Basis in einem geschlossenen Kreiskegel umfasst, während sich die laterale SA auf den Rest der Fläche des Kegels zwischen der Basis und seiner Spitze bezieht., Die zu berechnenden Gleichungen sowie die Gesamtmenge eines geschlossenen Kreiskegels sind unten dargestellt:

base SA = nr2
lateral SA = nr√r2 + h2
total SA = nr (r + √r2 + h2)
wobei r Radius und h Höhe

Athena hat sich kürzlich für die südostasiatische Kultur interessiert und ist besonders fasziniert von dem konischen Hut, der typischerweise als „Reishut“ bezeichnet wird und in einer Reihe südostasiatischer Länder häufig verwendet wird., Sie beschließt, eine eigene zu machen, und da sie eine sehr praktische Person ist, die nicht in Sentimentalität versunken ist, holt sie das Hochzeitskleid ihrer Mutter aus den dunklen Aussparungen des Kleiderschranks, in dem es sich befindet. Sie bestimmt die Oberfläche des Materials, das sie benötigt, um ihren Hut mit einem Radius von 1 Fuß und einer Höhe von 0,5 Fuß wie folgt zu erstellen:

A = π × 0,4√0,42 + 0,52 = 0.,805 ft2

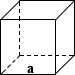
Würfel

Die Oberfläche eines Würfels kann berechnet werden, indem die Gesamtflächen seiner sechs quadratischen Flächen summiert werden:

SA = 6a2
wobei a ist Kantenlänge

Anne möchte ihrem jüngeren Bruder zu seinem Geburtstag einen Zauberwürfel geben, weiß aber, dass ihr Bruder eine kurze Aufmerksamkeitsspanne hat und leicht frustriert ist. Sie bestellt individuell einen Zauberwürfel, in dem alle Flächen schwarz sind, und muss für die Anpassung basierend auf der Oberfläche des Würfels mit einer Kantenlänge von 4 Zoll bezahlen.,

SA = 6 × 42 = 96 in2

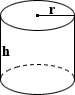
Zylindrischer Tank

Die Oberfläche eines geschlossenen Zylinders kann berechnet werden, indem die Gesamtflächen seiner Basis-und Seitenfläche summiert werden:

base SA = 2nr2
lateral SA = 2nrh
total SA = 2nr(r + h)wobei r Radius und h Höhe ist

Jeremy hat ein großes zylindrisches Aquarium, in dem er badet, weil er keine Duschen oder badewannen. Er ist neugierig, ob sein erhitztes Wasser schneller abkühlt als in einer Badewanne, und muss die Oberfläche seines zylindrischen Tanks mit einer Höhe von 5,5 Fuß und einem Radius von 3,5 Fuß berechnen.

gesamt SA = 2π × 3.,5(3,5 + 5,5) = 197.920 ft2

Rechteckiger Tank

Die Oberfläche eines rechteckigen Tanks ist die Summe der Fläche jeder seiner Flächen:

SA = 2lw + 2lh + 2wh
wobei l Länge, w Breite und h Höhe ist

Banane, die älteste Tochter einer langen Reihe von Bananenbauern, möchte ihrer verwöhnten, faulen kleinen Schwester Bananenbrot eine Lektion über Hoffnung und Erwartungen beibringen.. Banana-Bread hat die ganze Woche darüber geklagt, dass sie einen neuen Satz Schubladen für ihre neuen Batman-Actionfiguren haben möchte., Als solches kauft Banana ihr ein großes Barbie-Puppenhaus mit Küchenutensilien in limitierter Auflage, Backofen, Schürze und realistischen verrottenden Bananen für Batman., Sie packt diese in eine rechteckige Schachtel mit ähnlichen Abmessungen wie die Schublade, die Bananenbrot will, und muss die Menge an Geschenkpapier bestimmen, die sie benötigt, um ihre Präsentation des Geschenks der 3 ft × 4 ft × 5 ft Überraschung abzuschließen:

SA = (2 × 3 × 4) + (2 × 4 × 5) + (2 × 3 × 5) = 94 ft2

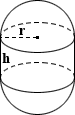
Kapsel

Die Oberfläche einer Kapsel kann durch Kombination der Oberflächenbereichsgleichungen für eine Kugel und der lateralen Oberfläche eines Zylinders bestimmt werden., Beachten Sie, dass die Oberfläche der Zylindersockel nicht enthalten ist, da sie keinen Teil der Oberfläche einer Kapsel umfasst. Die Gesamtoberfläche wird wie folgt berechnet:

SA = 4nr2 + 2nrh
wobei r Radius und h Höhe ist

Horatio stellt ein Placebo her, das vorgibt, die Individualität, das kritische Denken und die Fähigkeit einer Person zu schärfen objektiv und logisch verschiedene Situationen angehen., Er hat den Markt bereits getestet und festgestellt, dass eine große Mehrheit der Stichprobenpopulation keine dieser Eigenschaften aufweist und sehr bereit ist, sein Produkt zu kaufen, um sich in den Merkmalen weiter zu verankern, denen sie so verzweifelt entkommen wollen. Horatio muss die Oberfläche jeder Kapsel bestimmen, damit er sie mit einer übermäßigen Zuckerschicht überziehen und die für Zucker prädisponierten Zungen der Bevölkerung ansprechen kann, um sich auf sein nächstes Placebo vorzubereiten, das alle Formen von Diabetes mellitus „heilt“. Gegeben hat jede Kapsel r von 0,05 Zoll und h von 0,5 Zoll:

SA = 4π × 0.,052 + 2π × 0,05 × 0,5 = 0,188 in2

Kugelkappe

Die Oberfläche einer Kugelkappe basiert auf der Höhe des betreffenden Segments. Der mitgelieferte Rechner nimmt eine feste Kugel an und schließt die Basis der Kappe in die Berechnung der Oberfläche ein, wobei die Gesamtoberfläche die Summe der Fläche der Basis und der Seitenfläche der Kugelkappe ist. Wenn Sie mit diesem Rechner die Oberfläche einer Hohlkugel berechnen, subtrahieren Sie die Oberfläche der Basis., Bei zwei Werten Höhe, Kappenradius oder Basisradius kann der dritte Wert anhand der auf dem Volumenrechner angegebenen Gleichungen berechnet werden. Die Oberflächenbereichsgleichungen sind wie folgt:

sphärische Kappe SA = 2nRh
base SA = nr2
Total solid sphere SA = 2nRh + nr2
wobei R sphärischer Kappenradius ist, r Basisradius ist und h Höhe

Jennifer ist eifersüchtig auf den Globus, den ihr älterer Bruder Lawrence zu seinem Geburtstag erhalten hat. Da Jennifer zwei Drittel des Alters ihres Bruders hat, entscheidet sie, dass sie ein Drittel des Lebens ihres Bruders verdient., Nachdem sie die Handsäge ihres Vaters in den Werkzeugschuppen zurückgebracht hat, berechnet sie die Oberfläche ihres hohlen Teils des Globus mit R von 0,80 Fuß und h 0,53 Fuß wie unten gezeigt:

SA = 2π × 0,80 × 0,53 = 2.,664 ft2

Konisches Frustum

Die Oberfläche eines festen, rechten konischen Frustums ist die Summe der Flächen seiner beiden kreisförmigen Enden und der Fläche seiner Seitenfläche:

kreisförmiges Ende SA = π(R2 + r2)
seitliches SA = π(R+r)√(R-r)2 + h2
Gesamt SA = π(R2 + r2) + π(R+r)√(R-r)2 + h2
wobei R und r Radien sind von den Enden ist h Höhe

Paul macht für sein Science Fair-Projekt einen Vulkan in Form eines konischen Frustums., Paulus betrachtet Vulkanausbrüche als ein gewalttätiges Phänomen, und da er gegen alle Formen von Gewalt ist, beschließt er, seinen Vulkan in Form eines geschlossenen konischen Frustums zu machen, das nicht ausbricht. Obwohl sein Vulkan die Wissenschaftsrichter wahrscheinlich nicht beeindrucken wird, muss Paul immer noch die Oberfläche des Materials bestimmen, das er benötigt, um die Außenwand seines Vulkans mit R von 1 Fuß, r von 0,3 Fuß und h von 1,5 Fuß zu beschichten:

Gesamt SA = π (12 + 0,32) + π(1 + 0.3) √(1 – 0.3)2 + 1.52 = 10.,185 ft2

Ellipsoid

Die Berechnung der Oberfläche eines Ellipsoids hat keine einfache, exakte Formel wie ein Würfel oder eine andere einfachere Form. Der obige Rechner verwendet eine ungefähre Formel, die ein fast kugelförmiges Ellipsoid annimmt:

SA ≈ 4π 1,6√(a1.6b1.6 + a1.6c1.6 + b1.6c1.6)/3
wobei a, b und c die Achsen der Ellipse sind

Coltaine hat immer gerne gekocht und kürzlich ein Keramikmesser aus einem Wettbewerb gewonnen. Unglücklicherweise für seine Familie, die fast ausschließlich Fleisch isst, hat Coltaine seine Schneidtechnik an einer übermäßigen Menge Gemüse geübt., Anstatt sein Gemüse zu essen, starrt Coltaines Vater deprimiert auf seinen Teller und schätzt die Oberfläche der elliptischen Zucchinischnitte mit den Achsen 0,1, 0,2 und 0,35 Zoll:

SA ≈ 4π 1.6√(0.11.60.21.6 + 0.11.60.351.6 + 0.21.60.351.6)/3 = 0.562 in2

Quadratische Pyramide

Die Oberfläche einer quadratischen Pyramide besteht aus der Fläche ihrer quadratischen Basis und der Fläche jeder ihrer vier dreieckigen Flächen., Bei gegebener Höhe h und Kantenlänge a kann die Oberfläche mit den folgenden Gleichungen berechnet werden:

base SA = a2
lateral SA = 2a√(a/2)2 + h2
total SA = a2 + 2a√(a/2)2 + h2

Vonquaylas Klassenzimmer hat kürzlich den Bau eines Modells der Großen Pyramide von Gizeh abgeschlossen. Sie hat jedoch das Gefühl, dass das Modell nicht das Gefühl des architektonischen Wunders ausstrahlt, das das Original tut, und entscheidet, dass die Beschichtung mit „Schnee“ zumindest einen Aspekt des Staunens vermitteln würde., Sie berechnet die Oberfläche von geschmolzenem Zucker, die sie benötigen würde, um die Pyramide vollständig mit einer Kantenlänge a von 3 Fuß und einer Höhe h von 5 Fuß zu beschichten:

total SA = 32 + 2 × 3√(3/2)2 + 52 = 40.321 ft2

Im Gegensatz zu der Großen Pyramide von Gizeh, die seit Tausenden von Jahren steht, dauerte ihr Modell, das aus Graham-Crackern besteht und mit Zucker überzogen ist, nur wenige Tage.

Common Area Units

Unit	meter2
kilometer2	1,000,000
Zentimeter 2	0,0001
Millimeter 2	0.,000001
micrometer2	0.000000000001
hectare	10,000
mile2	2,589,990
yard2	0.83613
foot2	0.092903
inch2	0.00064516
acre	4,046.86