használja az alábbi számológépek kiszámításához a felület több közös formák., Surface Area
Cone Surface Area
Cube Surface Area
Cylindrical Tank Surface Area
Rectangular Tank Surface Area
Capsule Surface Area
Cap Surface Area
Please provide any two values below to calculate.,
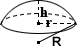
Csonka Kúp alakú Felület
Ellipsoid Felület
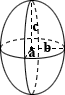
Négyzetes Piramis Felület
Kapcsolódó Kötet Számológép | Terület Számológép | testfelület Kalkulátor
A felület egy szilárd az intézkedés, hogy a teljes területet elfoglalták a felület egy tárgy., A számológépben szereplő összes objektumot részletesebben ismertetjük a Kötetkalkulátor és a Területkalkulátor oldalain. Mint ilyen, ez a számológép az objektumok felületének kiszámítására szolgáló egyenletekre, valamint ezen egyenletek használatára összpontosít. Kérjük, olvassa el a fent említett számológépek részletesebb minden egyes objektum.
Sphere
egy gömb felszíne (SA) a következő egyenlet segítségével számítható ki:
SA = 4nr2
ahol r a sugara
Xael nem szereti megosztani a csokoládé szarvasgomba senkivel., Amikor kap egy doboz Lindt szarvasgombát, elkezdi kiszámítani az egyes szarvasgomba felületét annak érdekében, hogy meghatározza a teljes felületet, amelyet meg kell nyalnia, hogy csökkentse annak valószínűségét, hogy bárki megpróbálja megenni a szarvasgomba. Tekintettel arra, hogy minden szarvasgomba sugara 0,325 hüvelyk:
SA = 4 × π × 0,3252 = 1,327 in2
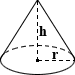
kúp
a kör alakú kúp felülete kiszámítható az egyes komponensek felületének összegzésével., A “base SA” kifejezés a kör, amely magában foglalja a bázis egy zárt kör alakú kúp, míg az oldalsó SA utal, hogy a többi terület a kúp között a bázis, a csúcsa., Az egyenletek kiszámításához az egyes, valamint a teljes SA egy zárt kör alakú kúp az alábbi táblázat mutatja:
alap SA = nr2
oldalsó SA = nr√r2 + h2
teljes SA = nr(r + √r2 + h2)
ahol r sugarú, h magasság
az Athena nemrégiben érdeklődik délkelet-Ázsiai kultúra, s különösen lenyűgözte a kúp alakú kalap, általában a továbbiakban a “rizs kalap,” amely az általánosan használt szám a délkelet-Ázsiai országban., Úgy dönt, hogy az egyik saját, és mivel egy nagyon praktikus ember nem belecsöppent a szentimentalitás, letölti anyja esküvői ruha a sötét mélyedések a szekrény, amelyben lakik. Meghatározza az anyag felületét, amelyet 1 láb sugarú, 0,5 láb magasságú kalapjának létrehozásához szükséges, az alábbiak szerint:
lateral SA = π × 0,4√0,42 + 0,52 = 0.,805 ft2
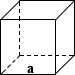
Kocka
A felület egy kocka lehet kiszámítani összegzésével a teljes területen a hat négyzetméter arcok:
SA = 6a2
hol a széle, hossza
Anne akarja, hogy az öccse egy Rubik-kocka a szülinapjára, de tudja, hogy a bátyja van egy rövid távú emlékezet, könnyen frusztrált. Ő rendeli Rubik kocka, amelyben az összes arc fekete, meg kell fizetni a Testreszabás alapján a felület a kocka él hossza 4 hüvelyk.,
SA = 6 × 42 = 96 in2
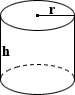
Hengeres Tartály
A felülete zárt henger lehet kiszámítani összegzésével a teljes területen a bázis, valamint oldalsó felület:
alap SA = 2nr2
oldalsó SA = 2nrh
teljes SA = 2nr(r + h)ahol r sugarú, h magasság
Jeremy egy nagy henger alakú akvárium hogy megfürdik, mert nem szereti, zuhanyzó vagy kád. Kíváncsi, hogy fűtött vize gyorsabban hűl-e, mint a kádban, és ki kell számítania hengeres tartályának felületét, magassága 5,5 láb, sugara pedig 3,5 láb.
összesen SA = 2π × 3.,5(3.5 + 5.5) = 197.920 ft2
téglalap alakú tartály
a téglalap alakú tartály felülete az egyes arcok területének összege:
SA = 2LW + 2LH + 2WH
ahol l hosszúság, w szélesség, h magasság
banán, a banántermesztők hosszú sorának legidősebb lánya, meg akarja tanítani rothadt kishúgát, banán-kenyeret, tanulság a reményről és az elvárásokról. Banana-kenyér már sürgető egész héten arról szeretnének egy új fiókos, hogy a ház az új Batman Akciófigurák., Mint ilyen, banán vásárol neki egy nagy Barbie baba ház korlátozott kiadású konyhai eszközök, Sütő, kötény, reális rothadó banán Batman., Ő csomagok, ezek egy téglalap alakú doboz hasonló méretű, mint a fiókban, hogy Banán-Kenyeret akar, meg kell határozni azt az összeget, csomagolópapír van szüksége, hogy befejezze a bemutatása, hogy az ajándék a 3 ft × 4 ft × 5 ft meglepetés:
SA = (2 × 3 × 4) + (2 × 4 × 5) + (2 × 3 × 5) = 94 ft2
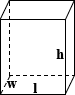
Kapszula
A felület egy kapszula lehet meghatározni ötvözi a felület egyenletek egy gömb, s az oldalsó felület egy henger., Vegye figyelembe, hogy a henger alapjainak felülete nem tartozik bele, mivel nem tartalmazza a kapszula felületének egy részét. A teljes felület a következőképpen számítják ki:
SA = 4nr2 + 2nrh
ahol r sugarú, h magasság
Horatio gyártási egy placebo azt állítja magáról, hogy élesíteni egy személy egyéniségét, a kritikus gondolkodás, valamint a képesség, hogy objektíven meg logikusan megközelítés különböző helyzetekben., Már tesztelte a piacot, és azt találta, hogy a mintapopuláció túlnyomó többsége nem mutat ilyen tulajdonságokat, és nagyon készen áll a termék megvásárlására, tovább kényszerítve magukat azon tulajdonságokon belül, amelyeket annyira kétségbeesetten próbálnak elmenekülni. Horatio kell meghatározni a terület minden egyes kapszula, így a kabát őket a túlzott réteg cukrot, a fellebbezést a cukor hajlamos nyelv a lakosság a felkészülés a következő placebo, hogy a “gyógyít” minden formája, a diabetes mellitus. Mivel minden kapszula r értéke 0,05 hüvelyk és h értéke 0,5 hüvelyk:
SA = 4π × 0.,052 + 2π × 0,05 × 0,5 = 0,188 in2
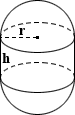
gömb alakú sapka
a gömb alakú kupak felülete a szóban forgó szegmens magasságán alapul. A megadott számológép szilárd gömböt feltételez, és a kupak alapját tartalmazza a felület kiszámításakor, ahol a teljes felület az alapterület és a gömb alakú kupak oldalfelületének összege. Ha ezt a számológépet egy üreges gömb felületének kiszámításához használja, vonja le az alap felületét., Tekintettel a magasság két értékére, a kupak sugara vagy az alap sugara, a harmadik érték a Térfogatkalkulátoron megadott egyenletek alapján számítható ki. A felületi egyenletek a következők:
gömb alakú sapka SA = 2NRH
alap SA = nr2
teljes szilárd gömb SA = 2NRH + Nr2
ahol R gömb alakú sapka sugara, r az alap sugara, h pedig magasság
Jennifer féltékeny a földgömbre, amelyet idősebb testvére, Lawrence kapott születésnapjára. Mivel Jennifer kétharmada a bátyja életkorának, úgy dönt, hogy megérdemli testvére földgömbjének egyharmadát., Miután visszatért az apja kezét, láttam, hogy a sufni, hogy kiszámítja a felülete neki, üreges részét a világon, R 0.80 láb, h 0.53 láb az alábbiak szerint:
SA = 2π × 0.80 × 0.53 = 2.,664 ft2
Kúpos Csonka
A felülete tömör, igaz kúpos csonka összege a területeken a két kör véget ér, továbbá az oldalsó arc:
a kör végén SA = π(R2 + r2)
oldalsó SA = π(R+r)√(R-r)2 + h2
teljes SA = π(R2 + r2) + π(R+r)√(R-r)2 + h2
hol R r vagy sugarak a vége, h magasság
Pál, hogy egy vulkán alakú kúpos csonka a tudományos kiállításra., Paul kilátás nyílik a vulkáni kitörések, mint egy erőszakos jelenség, hogy az erőszak valamennyi formája ellen, úgy dönt, hogy a vulkán formájában zárt kúp alakú csonka, hogy nem törnek ki. Bár a vulkán nem valószínű, hogy lenyűgözni a tudományos vásár bírók, Paul még mindig meg kell határoznia a felület az anyag, amire szüksége van, hogy kabát a külső fal a vulkán R 1 láb, r 0,3 láb, és h 1,5 láb:
összesen sa = π (12 + 0,32) + π(1 + 0.3) √(1 – 0.3)2 + 1.52 = 10.,185 ft2
ellipszoid
az ellipszoid felületének kiszámítása nem rendelkezik Egyszerű, pontos képlettel, például kockával vagy más egyszerűbb alakkal. A fenti számológép egy közelítő képletet használ, amely egy közel gömb alakú ellipszoidot feltételez:
sa ≈ 4π 1.6√(A1.6b1.6 + A1.6c1.6 + b1.6C1.6)/3
ahol az A, b és c az ellipszis tengelyei
Coltaine mindig is élvezte a főzést, és nemrégiben nyert egy kerámia kést egy versenyből. Sajnos a családja számára, aki szinte kizárólag húst eszik, a Coltaine túlzott mennyiségű zöldséggel gyakorolja vágási technikáját., A zöldségevés helyett coltaine apja megvetően bámul a tányérjára, és becsüli a cukkini elliptikus darabjainak felületét 0,1, 0,2 és 0,35 hüvelyk tengelyekkel:
sa ≈ 4π 1.6√(0.11.60.21.6 + 0.11.60.351.6 + 0.21.60.351.6)/3 = 0.562 in2
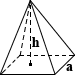
négyzet piramis
a négyzet alakú piramis felülete a négyzet alapterületéből és a négy háromszög alakú felületének területéből áll., Adott magasság h széle hossza egy, a terület kiszámítása a következő egyenlet segítségével:
alap SA = a2
oldalsó SA = 2a√(a/2)2 + h2
teljes SA = a2 + 2a√(a/2)2 + h2
Vonquayla osztálya a közelmúltban befejezett épület egy modell a Gízai Nagy Piramist. Úgy érzi azonban, hogy a modell nem kelti fel az építészeti csoda érzését, amelyet az eredeti tesz, és úgy dönt, hogy a “hóval” való bevonat legalább a csoda aspektusát adja., Ő kiszámítja a felület olvasztott cukor szüksége, hogy teljes mértékben kabát a piramis, széle, hossza egy 3 méter, magassága h, 5 méter:
a teljes SA = 32 + 2 × 3√(3/2)2 + 52 = 40.321 ft2
Ellentétben a Gízai Nagy Piramis, ami évezredek óta, a modell, a graham keksz bevont cukor, tartott csak napok kérdése.
közös körzeti egységek
| Unit | meter2 | ||
| kilométer2 | 1 000 000 | ||
| 0.0001 | |||
| mmeter2 | 0.,000001 | ||
| micrometer2 | 0.000000000001 | ||
| hectare | 10,000 | ||
| mile2 | 2,589,990 | ||
| yard2 | 0.83613 | ||
| foot2 | 0.092903 | ||
| inch2 | 0.00064516 | ||
| acre | 4,046.86 |
Leave a Reply