Radianos & DegreesReducing AnglesReference Ângulos
Purplemath
Na seção anterior, descobrimos que a primeira-círculo ângulo equivalentes para um dado ângulo de medidas. Outra coisa que podemos fazer com medidas de ângulo, mesmo aquelas cujas medidas estão na primeira volta, é encontrar o que é chamado de ângulo de “referência”.
O ângulo de referência é o ângulo que o ângulo dado faz com o eixo x., Independentemente de onde o ângulo termina (isto é, independentemente da localização do lado terminal do ângulo), o ângulo de referência mede a distância mais próxima desse lado terminal ao eixo x.
o conteúdo continua abaixo de
MathHelp.,com

Quando encontrar referência de ângulos, pode ser útil ter em mente que o positiva do eixo-x é 0° (e 360° ou 0 radianos (e 2π radianos); o positivo do eixo y é de 90° ou
radianos; o negativa do eixo x é de 180° ou π radianos; e o negativo do eixo y é de 270° ou radianos.
vamos começar com um exemplo fácil., O ângulo com a medida 30 ° iria grafo assim:
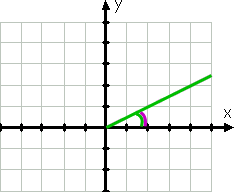
para grafagem, o lado inicial do ângulo é o eixo x positivo; o seu lado terminal é a linha verde, porque os ângulos são desenhados no sentido anti-horário. A linha verde curva mostra o ângulo dado.mesmo antes de ter desenhado o ângulo, eu saberia que o ângulo está no primeiro quadrante porque 30° está entre 0° e 90°. O ângulo de referência, mostrado pela linha roxa curva, é o mesmo que o ângulo dado.,
O ângulo 150°, obviamente, não é o mesmo que o ângulo 30°; é maior, e seu lado terminal está no segundo quadrante (porque 150° está entre 90° e 180°). No entanto, esse lado terminal é apenas 30° do eixo x negativo, como você pode ver pela linha púrpura no desenho:
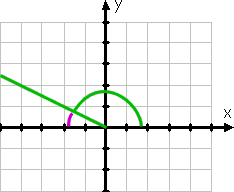
Uma vez que o lado terminal do 150° é apenas 30 graus do eixo x (negativo) (sendo 30 graus menos de 180°, que é o eixo x negativo), então o ângulo de referência (novamente mostrado pela linha roxa curva) é 30°.,continuando no sentido contrário ao dos ponteiros do relógio, podemos calcular 210°. O lado terminal deste ângulo, porque 210° está entre 180° e 270°, está no terceiro quadrante, e este lado está mais próximo do eixo x negativo. Porque 210 é 30 mais de 180, então o lado terminal deste ângulo é 30° passado (ou seja, abaixo) o eixo x negativo.
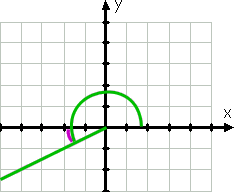
portanto, o ângulo de referência é, novamente, 30°.
aposto que você pode adivinhar qual seria o ângulo de referência para 330°., Uma vez que 330 é trinta menos de 360, e desde 360° = 0°, então o ângulo 330° é trinta graus abaixo (ou seja, menos de) do eixo x positivo, no quarto quadrante. O ângulo de referência é de 30°.
Afiliado
Afiliado

Repare-se como este último cálculo foi feito. Não tinha um gráfico. Acabei de fazer a aritmética na minha cabeça. Você deve desenhar gráficos enquanto precisar da ajuda, mas não tenha medo de começar a contar com a aritmética., Assim que apanhares o jeito, é muito simples.Nota: Como o ângulo de referência mede sempre a distância (positiva) do eixo dos x, também pode ser visto como sendo o ângulo equivalente do primeiro quadrante. Em outras palavras, para cada um dos exemplos acima, se meu manual definisse “ângulo de referência” como “o ângulo do primeiro quadrante com a mesma distância do eixo x”, então a linha “ângulo de referência” roxo (a linha roxa curva, mais um lado terminal) teria sido desenhada no primeiro quadrante.
de qualquer forma, o valor para o ângulo de referência será sempre o mesmo., Mas se você é obrigado a fazer um desenho mostrando o ângulo de referência, certifique-se de desenhá-lo no local que é considerado como “correto” para a sua classe.
-
encontrar o ângulo de referência para 1500°.
vou pegar na minha calculadora e fazer a divisão por 360° para “uma volta”:
1500 ÷ 360 = 4.16666…
portanto, há quatro ciclos, mais um pouco. Quanto são só os quatro ciclos?
4 × 360 = 1440
isso significa que a porção esquerda (0.16666… acima) representa mais 60 graus., Isto é menor que noventa graus, então o lado terminal do ângulo é à direita do eixo y positivo. Em seguida, o ângulo de referência está no primeiro quadrante e é igual a:
de 60°
Conteúdo Continua Abaixo
-
Encontrar o primeiro quadrante ângulo de referência para a 954°, e desenhar ambos os ângulos no mesmo sistema de eixos.
vou começar por reduzir este ângulo. Quantos ciclos se encaixam neste ângulo?
954 ÷ 360 = 2, 65
dois ciclos ajustam-se ao ângulo., Quanto da medida do ângulo é que esses dois ciclos ocupam?
360 × 2 = 720
então quanto resta?
954 – 720 = 234
o eixo x negativo é 180°, e o eixo y negativo é 270°. Este ângulo está entre esses valores, então está no terceiro quadrante, e estará mais próximo do eixo x negativo.a que distância? Será a distância entre o lado terminal do ângulo reduzido e o eixo x negativo:
234-180 = 54
então o ângulo de referência é:
54°
..,e o desenho é:
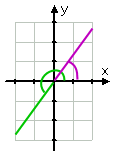
Afiliado
Observe que como eu desenhei o reduzido ângulo (o ângulo original, menos de dois ciclos) em verde, e então eu tirei o primeiro quadrante ângulo de referência em roxo. Quando você está fazendo desenhos que contêm duas (ou mais) partes distintas de informação, pode ser útil ter lápis coloridos na mão. Sim, usei lápis de cor na faculdade.
-
encontrar o ângulo de referência para radianos.,
Publicidade
Ok, isto está em radianos. Então eu vou precisar pensar em termos de 0 radianos e 2π radianos para o eixo x positivo, e π radianos para o eixo x negativo.o ângulo que me deram é radianos. Fazendo a divisão para converter a forma fracionária para a forma decimal (e ignorando o π para o momento), eu recebo:
16 ÷ 5 = 3.2
Em outras palavras,
radianos é igual a 3.2 π radianos. Um ciclo é 2π radians, então este é um pouco mais de metade de novo tanto quanto um ciclo., Em outras palavras, este ângulo vai um pouco além do eixo x negativo:
3.2 π – 2π = 1.2 π
mas a que distância está o lado terminal do eixo x negativo?
eu posso descobrir isso subtraindo-se o ângulo de medida da parte negativa do eixo x a partir do meu ângulo reduzida:
1.2 π – 1π
= 0.2 π
= (1/5)π
Isso me dá a distância entre o terminal do lado do (reduzida) o ângulo e o negativo ( – ) do eixo x em radianos. O ângulo de referência é:
-
encontrar o ângulo de referência para radianos.,
Uma vez que
é inferior a 2 mas mais do que , então este ângulo está no quarto quadrante, entre radianos e radianos 2π. Então é mais próximo do eixo x positivo. Mas quão perto? Eu vou subtrair para descobrir:
em Seguida, o ângulo de referência é:
Se você está trabalhando em graus ou em radianos, contanto que você saiba a medida do ângulo para o positivo e o negativo partes do eixo-x, você pode reduzir o ângulo (se necessário) e, em seguida, fazer o percurso de obter o ângulo de referência., Se você não tem certeza de seu trabalho, você pode desenhar o quadro para ter certeza. Mas se você ainda está precisando desenhar quando o teste está chegando, tente fazer alguma prática extra, porque o teste vai assumir que você não precisa de tempo para desenhar as imagens.
pode usar o elemento Mathway abaixo para praticar a procura da mediana. Tente o exercício introduzido, ou digite em seu próprio exercício. Em seguida, clique no botão e selecione “Encontrar o ângulo de referência” para comparar sua resposta com a de Mathway.,
por favor, aceite cookies de “preferências” para activar este elemento.
(clique em “toque para ver os passos” a serem dados diretamente ao site Mathway para uma atualização paga.)
URL: https://www.purplemath.com/modules/radians3.htm
Página 1Page 2Page 3
Leave a Reply