radiany & Kąty redukcyjne Kąty odniesienia
Purpurowy
w poprzedniej sekcji znaleźliśmy odpowiedniki kąta pierwszego okręgu dla podanych miar kąta. Inną rzeczą, którą możemy zrobić z miarami kąta, nawet tymi, których miary są w pierwszym okrążeniu, jest znalezienie tego, co nazywa się kątem „referencyjnym”.
kąt odniesienia to kąt, który dany kąt tworzy z osią X., Niezależnie od tego, gdzie kąt się kończy (tj. niezależnie od położenia strony zacisku kąta), kąt odniesienia mierzy najbliższą odległość tej strony zacisku do osi X.
treść nadal poniżej
MathHelp.,com

podczas wyszukiwania kątów odniesienia warto pamiętać, że dodatnia Oś x wynosi 0° (i 360° lub 0 radianów (i 2π radianów); dodatnia oś y wynosi 90° lub
radiany; ujemna oś x wynosi 180° lub π radiany; a ujemna oś Y wynosi 270° lub radiany.
Zacznijmy od prostego przykładu., Kąt o miarze 30° wykresuje się następująco:
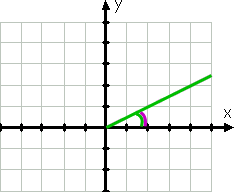
w przypadku wykresów początkową stroną kąta jest dodatnia oś x; jej końcową stroną jest zielona linia, ponieważ kąty są rysowane w kierunku przeciwnym do ruchu wskazówek zegara. Zakrzywiona zielona linia pokazuje podany kąt.
jeszcze przed rysowaniem kąta, wiedziałbym, że kąt jest w pierwszym kwadrancie, ponieważ 30° jest między 0° a 90°. Kąt odniesienia, pokazany przez zakrzywioną fioletową linię, jest taki sam jak podany kąt.,
Kąt 150°, oczywiście, nie jest taki sam jak kąt 30°; jest większy, a jego strona końcowa znajduje się w drugim kwadrancie (ponieważ 150° to między 90° a 180°). Jednak ta strona zacisku jest tylko 30° od ujemnej osi x, jak widać po fioletowej linii na rysunku:
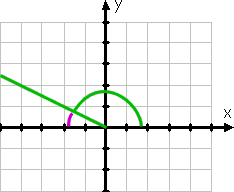
ponieważ strona zacisku 150° jest tylko trzydzieści stopni od (ujemnej) osi x (jest trzydzieści stopni mniej niż 180°, co jest ujemną osią x), wtedy kąt odniesienia (ponownie pokazany przez zakrzywioną fioletową linię) wynosi 30 stopni od (ujemnej) osi X (jest to trzydzieści stopni mniej niż 180°, co jest ujemną osią x).°.,
kontynuując w kierunku przeciwnym do ruchu wskazówek zegara, możemy wykreślić 210°. Kąt krańcowy tego kąta, ponieważ 210° znajduje się między 180° a 270°, znajduje się w trzecim kwadrancie, a ta strona jest najbliższa ujemnej osi X. Ponieważ 210 jest trzydzieści więcej niż 180, to kąt końcowy tego kąta jest o 30° obok (czyli poniżej) ujemnej osi X.
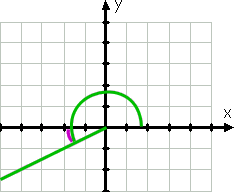
dlatego kąt odniesienia wynosi ponownie 30°.
założę się, że zgadniesz jaki byłby kąt odniesienia dla 330°., Ponieważ 330 jest trzydzieści mniej niż 360, a ponieważ 360° = 0°, to kąt 330° jest trzydzieści stopni poniżej (to jest, krótko) dodatniej osi x, w czwartym kwadrancie. Więc jego kąt odniesienia wynosi 30°.
Affiliate
Affiliate

. Nie miałem wykresu. Właśnie zrobiłem arytmetykę w mojej głowie. Powinieneś rysować wykresy tak długo, jak potrzebujesz pomocy, ale nie bój się zacząć polegać na arytmetyce., Kiedy już to zrozumiesz, będzie to bardzo proste.
Uwaga: Ponieważ kąt odniesienia zawsze mierzy (dodatnią) odległość od osi x, można go również postrzegać jako kąt równoramienny pierwszego kwadrantu. Innymi słowy, dla każdego z powyższych przykładów, gdyby mój podręcznik zdefiniował „kąt odniesienia” jako „kąt pierwszego kwadrantu o tej samej odległości od osi x”, to fioletowa linia „kąta odniesienia” (zakrzywiona fioletowa linia plus strona końcowa) zostałaby narysowana w pierwszym kwadrancie.
tak czy inaczej, wartość kąta odniesienia będzie zawsze taka sama., Ale jeśli musisz narysować obraz pokazujący kąt odniesienia, upewnij się, że narysujesz go w miejscu, które jest uważane za „poprawne” dla twojej klasy.
-
Znajdź kąt odniesienia dla 1500°.
wezmę kalkulator i zrobię podział przez 360° Dla „raz dookoła”:
1500 ÷ 360 = 4.16666…
więc są cztery cykle, plus trochę. Ile kosztuje tylko cztery cykle?
4 × 360 = 1440
oznacza to, że część lewa (0.16666… powyżej) reprezentuje kolejne sześćdziesiąt stopni., Jest to mniejsze niż dziewięćdziesiąt stopni, więc strona końcowa kąta znajduje się na prawo od dodatniej osi Y. Następnie kąt odniesienia znajduje się w pierwszym kwadrancie i jest równy:
60°
treść jest kontynuowana poniżej
-
Znajdź kąt odniesienia w pierwszym kwadrancie dla 954° i narysuj oba kąty na tym samym systemie osi.
zacznę od zmniejszenia tego kąta. Ile cykli mieści się pod tym kątem?
954 ÷ 360 = 2,65
dwa cykle mieszczą się pod kątem., Ile miary kąta zajmują te dwa cykle?
360 × 2 = 720
to ile zostało?
954 – 720 = 234
ujemna Oś x wynosi 180°, a ujemna oś y wynosi 270°. Ten kąt jest pomiędzy tymi wartościami, więc jest w trzecim kwadrancie i będzie najbliżej ujemnej osi X.
jak blisko? Będzie to odległość między stroną końcową zredukowanego kąta a ujemną osią x:
234 – 180 = 54
wtedy kąt odniesienia wynosi:
54°
…,a rysunek jest:
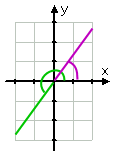
Affiliate
zauważ, jak narysowałem zmniejszony kąt (jako oryginalny kąt, mniej dwa cykle) w kolorze zielonym, a następnie narysowałem pierwszy kwadrant kąt odniesienia w Kolorze Fioletowym. Gdy robisz rysunki, które zawierają dwa (lub więcej) różne informacje, pomocne może być posiadanie pod ręką kolorowych kredek. Tak, na studiach używałam kolorowych ołówków.
-
Znajdź kąt odniesienia dla radianów.,
Reklama
ok, to jest w radianach. Więc będę musiał myśleć w kategoriach 0 radianów i 2π radianów dla dodatniej osi x i π radianów dla ujemnej osi X.
kąt jaki mi dali to
radiany. Wykonując podział, aby przekształcić postać ułamkową do postaci dziesiętnej (i ignorując na razie π), otrzymuję:
16 ÷ 5 = 3.2
innymi słowy,
radiany są równe 3.2 π radianów. Jeden cykl to 2π radianów, więc jest to nieco ponad połowa-znowu tyle, co jeden cykl., Innymi słowy, kąt ten przechodzi nieco poza ujemną oś x:
3.2 π – 2π = 1.2 π
ale jak daleko jest strona końcowa od ujemnej osi x?
mogę to zrozumieć, odejmując miarę kąta ujemnej osi x od mojego zredukowanego kąta:
1.2 π-1π
= 0.2 π
= (1/5)π
to daje mi odległość między stroną końcową (zredukowanego) kąta a (ujemną) osi x w radianach. Kąt odniesienia to:
-
Znajdź kąt odniesienia dla radianów.,
ponieważ
jest mniejsze niż 2 , ale więcej niż, to kąt ten znajduje się w czwartym kwadrancie, między radianami I 2π radianami. Wtedy jest najbliżej dodatniej osi X. Ale jak blisko? Odejmuję, aby się dowiedzieć:
wtedy kąt odniesienia wynosi:
niezależnie od tego, czy pracujesz w stopniach, czy w radianach, o ile znasz miary kąta dla dodatnich i ujemnych części osi x, możesz zmniejszyć kąt (w razie potrzeby), a następnie wykonywać odejmowania, aby uzyskać kąt odniesienia., Jeśli nie jesteś pewien swojej pracy, możesz narysować obraz, aby mieć pewność. Ale jeśli nadal potrzebujesz rysować zdjęcia, gdy zbliża się test, spróbuj wykonać dodatkową praktykę, ponieważ test zakłada, że nie potrzebujesz czasu, aby narysować zdjęcia.
możesz użyć widżetu Mathway poniżej, aby ćwiczyć znajdowanie mediany. Wypróbuj wprowadzone ćwiczenie lub wpisz własne ćwiczenie. Następnie kliknij przycisk i wybierz „Znajdź kąt odniesienia”, aby porównać odpowiedź z odpowiedzią Mathwaya.,
proszę zaakceptować pliki cookie „preferencje”, aby włączyć ten widget.
(kliknij „Dotknij, aby wyświetlić kroki”, aby przejść bezpośrednio do strony Mathway, aby uzyskać płatną aktualizację.)
URL: https://www.purplemath.com/modules/radians3.htm
strona 1 strona 2 strona 3
Leave a Reply