Radians&DegreesReducing AnglesReference Angles
前のセクションでは、与えられた角度に相当する最初の円の角度を見つけました対策。 角度測定で行うことができるもう一つのことは、最初のゴーアラウンドにあるものでさえ、”参照”角度と呼ばれるものを見つけることです。
基準角度は、与えられた角度がx軸に対して行う角度です。, 角度がどこで終わるかにかかわらず（つまり、角度の端子側の位置にかかわらず）、基準角度は、その端子側のx軸に対する最も近い距離を測定します。
コンテンツは以下のように続きます
基準角度を見つけるときは、正のx軸は0°（および360°または0ラジアン（および2πラジアン）であり、正のy軸は90°または
ラジアンであり、負のx軸は180°または負のy軸は270°またはラジアンです。
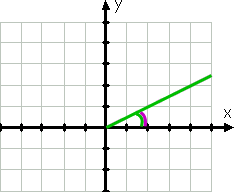
簡単な例から始めましょう。, メジャー30°の角度は次のようにグラフ化されます。
グラフ化する場合、角度の初期側は正のx軸です。角度は反時計回りに描画されるため、端子側は緑色の線です。 曲線の緑色の線は、与えられた角度を示しています。
角度を描く前でさえ、30°が0°から90°の間にあるため、角度が最初の象限にあることがわかっていました。 曲線の紫色の線によって示される基準角度は、指定された角度と同じです。,
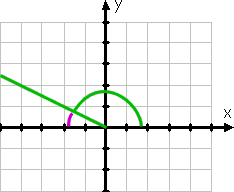
角度150°は、明らかに、角度30°と同じではありません;それはより大きく、その端子側は第二象限にあります（150°は90°と180°の間にあるため）。 しかし、その端子側は負のx軸からわずか30°です。
150°の端子側は（負の）x軸からわずか三〇度であるため（負のx軸である180°未満である）、基準角度（再び湾曲した紫色の線で示される）は30°です。,
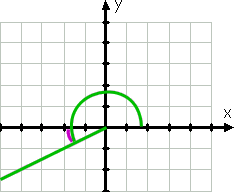
反時計回りに続けると、210°をグラフ化できます。 この角度の端子側は、210°が180°から270°の間であるため、第三象限にあり、この側は負のx軸に最も近い。 210は180よりも大きいので、この角度の端子側は負のx軸を30°過ぎている（つまり、下にある）。
したがって、基準角度は再び30°です。
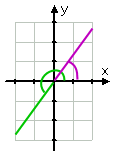
私はあなたが330°の基準角度が何であるかを推測することができます賭けます。, 330は360より三十未満であり、360°=0°であるため、角度330°は正のx軸より三十度下（つまり、四分円の短い）になります。 したがって、その基準角度は30°です。
アフィリエイト
アフィリエイト
この最後の計算がどのように行われたかに注意してください。 私はグラフを持っていませんでした。 私はちょうど私の頭の中で算術をしました。 あなたは助けが必要な限りグラフを描くべきですが、算術に頼り始めることを恐れないでください。, あなたはこれのこつを取得したら、それは本当にかなり簡単です。
注意：基準角度は常にx軸からの（正の）距離を測定するため、第一象限の等価角度と見なすこともできます。 言い換えれば、上記の各例について、私の教科書が”基準角度”を”x軸から同じ距離の第一象限角度”と定義した場合、紫色の”基準角度”線（湾曲した紫色の
いずれにしても、基準角度の値は常に同じになります。, ただし、参照角度を示す画像を描画する必要がある場合は、クラスの”正しい”とみなされる場所に描画してください。
私は電卓をつかんで、”一度”のために360°除算を行います：
1500÷360=4.16666。..
だから、四つのサイクルに加えて少しがあります。 四つのサイクルだけでどれくらいですか？
4×360=1440
つまり、残りの部分（0.16666。.. 上記）は別の六十度を表します。, これは九十度よりも小さいので、角度の端子側は正のy軸の右側にあります。 次に、基準角度は最初の象限にあり、次のようになります。
60°
コンテンツは次のように続きます。
私はこの角度を減らすことから始めましょう。 どのように多くのサイクル以内に収まるこの角度は?
954÷360=2.65
二つのサイクルが角度内に収まります。, これらの二つのサイクルは、角度の尺度のどのくらいを取るのですか？
360×2=720
それでは、どれくらい残っていますか？
954-720=234
負のx軸は180°、負のy軸は270°です。 この角度は、それらの値の間にあるので、それは第三象限にあり、負のx軸に最も近くなります。
どのくらい近いですか？ これは、縮小された角度の端子側と負のx軸との間の距離になります。
234-180=54
基準角度は次のとおりです。
54°
。..,そして、図面は次のとおりです。
アフィリエイト
紫の象限基準角度。 二つ（またはそれ以上）異なる情報を含む図面を作成しているときは、色鉛筆を手元に置くと役に立ちます。 はい、私は大学で色鉛筆を使用しました。
広告
さて、これはラジアン単位です。 したがって、正のx軸に対しては0ラジアンと2πラジアン、負のx軸に対してはπラジアンで考える必要があります。
彼らが私に与えた角度は
ラジアンです。 小数形式を小数形式に変換するために除算を行うと（そして現時点ではθを無視して）、次のようになります。
16÷5=3.2
言い換えれば、
ラジアンは3.2πラジアンに等しくなります。 一つのサイクルは2πラジアンであるため、これは一つのサイクルと同じくらい半分よりも少し多くなります。, 言い換えれば、この角度は負のx軸を少し過ぎています：
3.2π-2π=1.2π
しかし、負のx軸から端子側はどのくらい離れていますか？
減少角度から負のx軸の角度尺度を減算することで、これを理解できます。
1.2μ-1μ
=0.2μ
=(1/5)μ
これは、（減少角度の端子側と（負の）x軸との間の距離をラジアン単位で示します。 基準角度は次のとおりです。
は2より小さいがより大きいので、この角度は第四象限にあり、ラジアンと2πラジアンの間にあります。 それからそれは正のx軸に最も近いです。 がか? 私は見つけるために減算します：
基準角度は次のとおりです。
角度がx軸の正と負の部分の角度の尺度を知っている限り、角度を減らしてから、基準角度を得るために減算を行うことができます。, あなたの仕事がわからない場合は、確実に絵を描くことができます。 しかし、テストが来ているときにまだ絵を描く必要がある場合は、テストでは絵を描く時間が必要ないと仮定するため、余分な練習をしてみてくださ
あなたは中央値を見つける練習するために以下のMathwayウィジェットを使用することができます。 入力された運動を試してみるか、独自の運動を入力してください。 次に、ボタンをクリックして”基準角度を見つける”を選択して、答えをMathwayと比較します。,
このウィジェットを有効にするには、”環境設定”クッキーを受け入れてください。
（有料アップグレードのためにMathwayサイトに直接取られるように”ステップを表示するにはタップ”をクリックしてください。)
URL:https://www.purplemath.com/modules/radians3.htm
ページ1ページ2ページ3
Leave a Reply