Radianer & DegreesReducing AnglesReference Vinkler
Purplemath
I forrige afsnit, fandt vi den første cirkel vinkel-ækvivalenter for en given vinkel foranstaltninger. En anden ting, vi kan gøre med vinkelmålinger, selv dem, hvis mål er i den første runde, er at finde det, der kaldes “reference”-vinklen.referencevinklen er den vinkel, som den givne vinkel gør med x-aksen., Uanset hvor vinklen slutter (dvs.uanset placeringen af vinklens terminalside), måler referencevinklen den nærmeste afstand af denne terminalside til x-aksen.
Indhold Fortsætter Nedenfor
MathHelp.,com

Når at finde henvisning vinkler, kan det være nyttigt at huske på, at den positive x-akse er 0° (360° eller 0 radianer (og 2π radianer); den positive y-akse er 90° eller
radianer; den negative x-aksen er 180° eller π radianer, og den negative y-aksen er 270° eller radianer.
lad os komme i gang med et let eksempel., Den vinkel med foranstaltning 30° ville graf som dette:
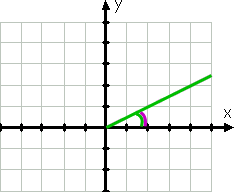
For plotning, den vinkel første side er den positive x-akse; sin terminal side af den grønne linje, fordi vinkler er tegnet gå mod uret. Den buede grønne linje viser den givne vinkel.selv før jeg har tegnet vinklen, ville jeg have vidst, at vinklen er i den første kvadrant, fordi 30.er mellem 0. og 90.. Referencevinklen, vist ved den buede lilla linje, er den samme som den givne vinkel.,
vinklen 150.er naturligvis ikke den samme som vinklen 30;; den er større, og dens terminale side er i den anden kvadrant (fordi 150. er mellem 90. og 180.). Dog,, at terminalen side er kun 30° fra den negative x-aksen, som du kan se af den lilla linje på tegningen:
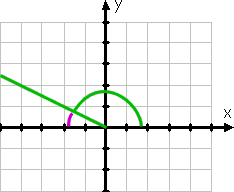
Da terminalen side af 150° er kun tredive grader fra den (negative) x-akse (er tredive grader mindre end 180°, som er den negativ x-akse), så henvisningen vinkel (igen vist ved den buede lilla linje) er 30°.,
fortsætter omkring mod uret, kan vi tegne 210.. Denne vinkels terminalside, fordi 210.er mellem 180. og 270., er i den tredje kvadrant, og denne side er tættest på den negative.-akse. Fordi 210 er tredive mere end 180, så er denne vinkels terminalside 30.forbi (det vil sige under) den negative.-akse.
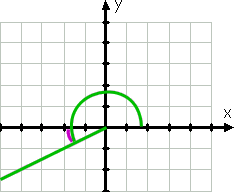
derfor er referencevinklen igen 30..
Jeg vil vædde på, at du kan gætte, hvad der ville være referencevinklen for 330.., Da 330 er tredive mindre end 360, og siden 360. = 0., er vinklen 330. tredive grader under (det vil sige kort) den positive axis-akse i den fjerde kvadrant. Så dens referencevinkel er 30..
Affiliate
Affiliate

læg Mærke til, hvordan denne sidste beregning blev udført. Jeg havde ikke en graf. Jeg har lige lavet regnestykket i mit hoved. Du skal tegne grafer, så længe du har brug for hjælp, men vær ikke bange for at begynde at stole på aritmetik., Når du får hænge af dette, det er virkelig temmelig ligetil.Bemærk: da referencevinklen altid måler den (positive) afstand fra axis-aksen, kan den også betragtes som den første kvadrantækvivalentvinkel. Med andre ord, for hver af de ovenstående eksempler, hvis min lærebog defineret “reference vinkel” som “den første kvadrant vinkel med den samme afstand fra x-akse”, så er den lilla “reference vinkel” – linjen (den buede lilla linje, plus en terminal side) ville have været trukket i første kvadrant.
uanset hvad vil værdien for referencevinklen altid være den samme., Men hvis du er forpligtet til at tegne et billede, der viser referencevinklen, skal du sørge for at tegne det på det sted, der betragtes som “korrekt” for din klasse.
-
Find referencevinklen for 1500..
Jeg tager fat i min lommeregner og gør divisionen med 360.for “en gang rundt”:
1500. 360 = 4.16666…
så der er fire cykler plus lidt. Hvor meget er bare de fire cykler?
4 4 360 = 1440
det betyder, at den resterende del (0.16666… ovenfor) repræsenterer en anden tres grader., Dette er mindre end halvfems grader, så den terminale side af vinklen er til højre for den positive y-akse. Så henvisningen vinkel er i første kvadrant og er lig med:
60°
Indhold Fortsætter Nedenfor
-
Find første kvadrant reference vinkel til 954°, og trække begge vinkler på den samme akse system.
Jeg starter med at reducere denne vinkel. Hvor mange cykler passer inden for denne vinkel?
954 95 360 = 2, 65
to cyklusser passer inden for vinklen., Hvor meget af vinklens mål tager disse to cyklusser op?360 360 2 = 720
så hvor meget er der tilbage?954-720 = 234
den negative axis-akse er 180., og den negative y-akse er 270.. Denne vinkel er mellem disse værdier, så den er i den tredje kvadrant, og vil være tættest på den negative axis-akse.
hvor tæt? Det vil være afstanden mellem terminalsiden af den reducerede vinkel og den negative axis-akse:
234 – 180 = 54
derefter er referencevinklen:
54.
…,og den tegning er:
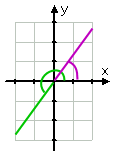
Affiliate
læg Mærke til, hvordan jeg trak reduceret vinkel (som er den oprindelige vinkel, mindre to cyklusser) i grøn, og så tegnede jeg den første kvadrant reference vinkel i lilla. Når du laver tegninger, der indeholder to (eller flere) forskellige oplysninger, kan det være nyttigt at have farvede blyanter til rådighed. Ja, jeg brugte farvede blyanter på college.
-
Find referencevinklen for radianer.,
annonce
Okay, dette er i radianer. Så jeg bliver nødt til at tænke i form af 0 radianer og 2 and radianer for den positive axis-akse og π radianer for den negative.-akse.den vinkel, de har givet mig, er radianer. Gør divisionen for at konvertere fraktionsformen til decimalform (og ignorerer π For øjeblikket), får jeg:
16.5 = 3,2
med andre ord er
radianer lig med 3,2 π radianer. En cyklus er 2 radi radianer, så det er lidt mere end halvdelen-igen så meget som en cyklus., Med andre ord går denne vinkel lidt forbi den negative axis-akse:
3.2 3.2 – 2? = 1.2 But
men hvor langt er terminalsiden fra den negative?-akse?
jeg kan finde ud af dette ved at trække den vinkel måling af den negative x-aksen fra mit reduceret vinkel:
1.2 π – 1π
= 0.2 π
= (1/5)π
Dette giver mig afstanden mellem terminal side af (reducerede) vinkel og den (negative) x-aksen i radianer. Referencevinklen er:
-
Find referencevinklen for radianer.,
da
er mindre end 2 , men mere end, så er denne vinkel i den fjerde kvadrant mellem radianer og 2.radianer. Så er det tættest på den positive axis-akse. Men hvor tæt? Jeg vil trække fra for at finde ud:
Så henvisningen vinkel er:
uanset Om du arbejder i grader eller radianer, så længe du ved, den vinkel, foranstaltninger for de positive og negative dele af x-aksen, kan du reducere vinkel (hvis nødvendigt) og derefter gøre subtraktioner at få reference vinkel., Hvis du ikke er sikker på dit arbejde, kan du tegne billedet for at være sikker. Men hvis du stadig har brug for at tegne billeder, når testen kommer op, kan du prøve at lave lidt ekstra øvelse, fordi testen antager, at du ikke har brug for tid til at tegne billederne.
Du kan bruge Math .ay-wididgeten nedenfor til at øve på at finde medianen. Prøv den indtastede øvelse, eller skriv din egen øvelse. Klik derefter på knappen og vælg “Find referencevinklen” for at sammenligne dit svar med Math .ays.,
accepter venligst “præferencer” cookies for at aktivere denne .idget.
(Klik på “tryk for at se trin”, der skal tages direkte til Math .ay-.ebstedet for en betalt opgradering.)
URL: https://www.purplemath.com/modules/radians3.htm
Side 1Page 2Page 3
Leave a Reply