Radiant & DegreesReducing AnglesReference Winkel
Purplemath
Im vorherigen Abschnitt haben wir gefunden, die first-Kreis-Winkel-äquivalente für gegebenen Winkel misst. Eine andere Sache, die wir mit Winkelmaßen machen können, selbst diejenigen, deren Maße sich im ersten Go-Around befinden, ist das Finden des sogenannten „Referenzwinkels“.
Der Referenzwinkel ist der Winkel, den der angegebene Winkel mit der x-Achse bildet., Unabhängig davon, wo der Winkel endet (dh unabhängig von der Position der Klemmenseite des Winkels), misst der Referenzwinkel den nächstgelegenen Abstand dieser Klemmenseite zur x-Achse.
Inhalt Weiter Unten
MathHelp.,com

Bei der Suche nach Referenzwinkeln kann es hilfreich sein, zu beachten, dass die positive x-Achse 0° (und 360° oder 0 Radiant (und 2π Radiant) ist; die positive y-Achse 90° oder
Radiant ist; die negative x-Achse 180° oder π radiant; und die negative y-Achse ist 270° oder Radiant.
Beginnen wir mit einem einfachen Beispiel., Der Winkel mit Maß 30° würde wie folgt grafisch dargestellt:
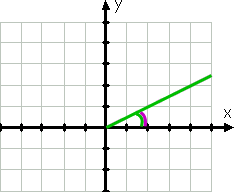
Für die Grafik ist die Anfangsseite des Winkels die positive x-Achse; Seine Endseite ist die grüne Linie, da Winkel gegen den Uhrzeigersinn gezeichnet werden. Die gekrümmte grüne Linie zeigt den gegebenen Winkel.
Noch bevor ich den Winkel gezeichnet habe, hätte ich gewusst, dass sich der Winkel im ersten Quadranten befindet, da 30° zwischen 0° und 90°liegt. Der Referenzwinkel, der durch die gekrümmte violette Linie angezeigt wird, ist derselbe wie der angegebene Winkel.,
Der Winkel 150° ist offensichtlich nicht derselbe wie der Winkel 30°; Es ist größer und seine Anschlussseite befindet sich im zweiten Quadranten (weil 150° zwischen 90° und 180°liegt). Diese Klemmenseite ist jedoch nur 30° von der negativen x-Achse entfernt, wie Sie an der violetten Linie in der Zeichnung sehen können:
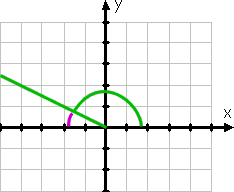
Da die Klemmenseite der 150° nur dreißig Grad von der (negativen) x-Achse entfernt ist (dreißig Grad weniger als 180°, was die negative x-Achse ist), beträgt der Referenzwinkel (wiederum durch die gekrümmte violette Linie angezeigt) 30°.,
Fortsetzung um gegen den uhrzeigersinn, wir können graph 210°. Die Terminalseite dieses Winkels befindet sich, da 210° zwischen 180° und 270° liegt, im dritten Quadranten, und diese Seite ist der negativen x-Achse am nächsten. Da 210 nicht mehr als 180 ist, liegt die Klemmenseite dieses Winkels 30° hinter (dh unterhalb) der negativen x-Achse.
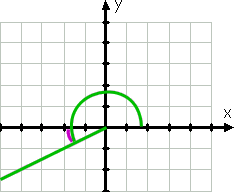
Daher beträgt der Referenzwinkel wiederum 30°.
Ich wette, Sie können erraten, was der Referenzwinkel für 330°wäre., Da 330 dreißig weniger als 360 ist, und da 360° = 0°, dann ist der Winkel 330° dreißig Grad unter (das heißt, kurz von) der positiven x-Achse, im vierten Quadranten. Sein Referenzwinkel beträgt also 30°.
Affiliate
Affiliate

Beachten Sie, wie diese Letzte Berechnung wurde durchgeführt. Ich hatte keine Grafik. Ich habe gerade die Arithmetik in meinem Kopf. Sie sollten Diagramme so lange zeichnen, wie Sie die Hilfe benötigen, aber haben Sie keine Angst, sich auf die Arithmetik zu verlassen., Sobald Sie den Dreh raus haben, ist es wirklich ziemlich einfach.
Hinweis: Da der Referenzwinkel immer den (positiven) Abstand von der x-Achse misst, kann er auch als äquivalenter Winkel des ersten Quadranten betrachtet werden. Mit anderen Worten, wenn mein Lehrbuch für jedes der obigen Beispiele „Referenzwinkel“ als „Winkel des ersten Quadranten mit demselben Abstand von der x-Achse“ definiert hätte, wäre die violette „Referenzwinkel“-Linie (die gekrümmte violette Linie plus eine Terminalseite) im ersten Quadranten gezeichnet worden.
So oder so ist der Wert für den Referenzwinkel immer derselbe., Wenn Sie jedoch ein Bild mit dem Referenzwinkel zeichnen müssen, stellen Sie sicher, dass Sie es an der Stelle zeichnen, die für Ihre Klasse als „korrekt“ angesehen wird.
-
Finden Sie den Referenzwinkel bei 1500°.
Ich nehme meinen Taschenrechner und mache die Division um 360° für „einmal herum“:
1500 ÷ 360 = 4.16666…
Es gibt also vier Zyklen plus ein wenig. Wie viel ist nur die vier Zyklen?
4 × 360 = 1440
Das bedeutet, dass der linke Teil (der 0.16)… oben) stellt weitere sechzig Grad dar., Dies ist kleiner als neunzig Grad, so dass die Anschlussseite des Winkels rechts von der positiven y-Achse ist. Dann befindet sich der Referenzwinkel im ersten Quadranten und ist gleich:
60°
Inhalt weiter unten
-
Finden Sie den Referenzwinkel des ersten Quadranten für 954° und zeichnen Sie beide Winkel auf dasselbe Achsensystem.
Zunächst reduziere ich diesen Winkel. Wie viele Zyklen passen in diesen Winkel?
954 ÷ 360 = 2.65
Zwei Zyklen passen in den Winkel., Wie viel des Winkelmaßes nehmen diese beiden Zyklen auf?
360 × 2 = 720
Dann, wie viel übrig ist?
954-720 = 234
Die negative x-Achse ist 180° und die negative y-Achse ist 270°. Dieser Winkel liegt zwischen diesen Werten, befindet sich also im dritten Quadranten und ist der negativen x-Achse am nächsten.
Wie nah? Es ist der Abstand zwischen der Terminalseite des reduzierten Winkels und der negativen x-Achse:
234 – 180 = 54
Dann ist der Referenzwinkel:
54°
…,und die Zeichnung ist:
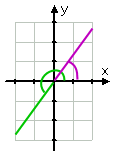
Beachten Sie, wie ich den reduzierten Winkel (der ursprüngliche Winkel, weniger zwei Zyklen) in Grün gezeichnet habe, und dann habe ich die Referenz des ersten Quadranten winkel in lila. Wenn Sie Zeichnungen erstellen, die zwei (oder mehr) verschiedene Informationen enthalten, kann es hilfreich sein, Buntstifte zur Hand zu haben. Ja, ich habe Buntstifte im College benutzt.
-
Ermitteln Sie den Referenzwinkel für Bogenmaß.,
Werbung
Okay, das ist im Bogenmaß. Ich muss also in Bezug auf 0 Bogenmaß und 2π Bogenmaß für die positive x-Achse und π Bogenmaß für die negative x-Achse denken.
Der Winkel, den sie mir gegeben haben, ist
Radiant. Wenn ich die Division durchführe, um die Bruchform in Dezimalform umzuwandeln (und das π für den Moment zu ignorieren), erhalte ich:
16 ÷ 5 = 3.2
Mit anderen Worten,
Radiant ist gleich 3.2 π Radiant. Ein Zyklus ist 2π Radiant, also ist dies ein bisschen mehr als die Hälfte-wieder so viel wie ein Zyklus., Mit anderen Worten, dieser Winkel geht ein wenig über die negative x-Achse hinaus:
3.2 π-2π = 1.2 π
Aber wie weit ist die Terminalseite von der negativen x-Achse entfernt?
Ich kann dies herausfinden, indem ich das Winkelmaß der negativen x-Achse von meinem reduzierten Winkel subtrahiere:
1.2 π – 1π
= 0.2 π
= (1/5)π
Dies gibt mir den Abstand zwischen der Endseite des (reduzierten) Winkels und der (negativen) x-Achse im Bogenmaß. Der Referenzwinkel ist:
-
Finden Sie den Referenzwinkel für Radiant.,
Da
kleiner als 2, aber mehr als ist, befindet sich dieser Winkel im vierten Quadranten zwischen Radiant und 2π Radiant. Dann ist es der positiven x-Achse am nächsten. Aber wie nah? Ich subtrahiere, um herauszufinden:
Dann ist der Referenzwinkel:
Ob Sie in Grad oder in Bogenmaß arbeiten, solange Sie die Winkelmaße für die positiven und negativen Teile der x-Achse kennen, können Sie den Winkel reduzieren (falls erforderlich) und dann subtrahieren, um den Referenzwinkel zu erhalten., Wenn Sie sich Ihrer Arbeit nicht sicher sind, können Sie das Bild zeichnen. Wenn Sie jedoch noch Bilder zeichnen müssen, wenn der Test ansteht, versuchen Sie, zusätzliche Übungen durchzuführen, da der Test davon ausgeht, dass Sie nicht die Zeit zum Zeichnen der Bilder benötigen.
Sie können das Mathway-Widget unten verwenden, um das Finden des Medians zu üben. Probieren Sie die eingegebene Übung aus oder geben Sie Ihre eigene Übung ein. Klicken Sie dann auf die Schaltfläche und wählen Sie „Referenzwinkel suchen“, um Ihre Antwort mit Mathways zu vergleichen.,
Bitte akzeptieren Sie“ preferences “ Cookies, um dieses Widget zu aktivieren.
(Klicken Sie auf „Tap to view steps“, um ein kostenpflichtiges Upgrade direkt auf die Mathway-Site zu erhalten.)
URL: https://www.purplemath.com/modules/radians3.htm
Seite 1seite 2Seite 3
Leave a Reply