
Sir Isaac Newton (1643-1727)
w porywającej atmosferze XVII-wiecznej Anglii, wraz z ekspansją Imperium Brytyjskiego w pełnym rozkwicie, wielkie stare uniwersytety, takie jak Oxford i Cambridge, produkowały wielu wielkich naukowców i matematyków. Ale największym z nich był niewątpliwie Sir Isaac Newton.,
fizyk, matematyk, astronom, filozof przyrody, alchemik i teolog, Newton jest uważany przez wielu za jednego z najbardziej wpływowych ludzi w historii ludzkości. Jego publikacja z 1687 roku, ” Philosophiae Naturalis Principia Mathematica „(zwykle nazywana po prostu” Principia”), jest uważana za jedną z najbardziej wpływowych książek w historii nauki i zdominowała naukowe spojrzenie na fizyczny wszechświat przez następne trzy stulecia.,
chociaż w dużej mierze synonim w umysłach ogółu społeczeństwa z grawitacji i historii jabłoni, Newton pozostaje gigantem w umysłach matematyków wszędzie (na równi z wszech czasów Wielkich jak Archimedes i Gauss), a on znacznie wpłynął na późniejszą ścieżkę rozwoju matematycznego.
w ciągu dwóch cudownych lat, w czasie Wielkiej Plagi 1665-6, Młody Newton opracował nową teorię światła, odkrył i obliczył grawitację i był pionierem Rewolucyjnego nowego podejścia do matematyki: rachunku nieskończoności., Jego teoria rachunku opiera się na wcześniejszych pracach jego kolegów Anglików Johna Wallisa i Isaaca Barrowa, a także na pracach takich kontynentalnych matematyków, jak René Descartes, Pierre de Fermat, Bonaventura Cavalieri, Johann van Waveren Hudde i Gilles Personne de Roberval. W przeciwieństwie do geometrii statycznej Greków, obliczenia pozwoliły matematykom i inżynierom zrozumieć ruch i dynamiczne zmiany w zmieniającym się świecie wokół nas, takie jak orbity planet, ruch płynów itp.,
średnie nachylenie krzywej
różnicowanie (pochodna) przybliża nachylenie krzywej w miarę zbliżania się interwału do zera
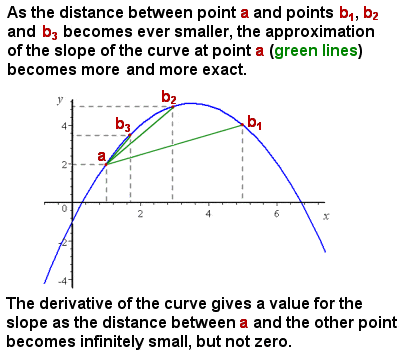
początkowy problem, z którym zmagał się Newton, polegał na tym, że chociaż łatwo było przedstawić i obliczyć średnie nachylenie krzywej (na przykład rosnącą prędkość obiektu na wykresie czasowo-odległości), nachylenie krzywej stale się zmieniało i nie było sposobu na podanie dokładnego nachylenia w jednym punkcie krzywej, tj., skutecznie nachylenie linii stycznej do krzywej w tym punkcie.
intuicyjnie nachylenie w danym punkcie można przybliżać przyjmując średnie nachylenie („wzrost nad biegiem”) coraz mniejszych segmentów krzywej. Ponieważ rozpatrywany odcinek krzywej zbliża się do zera (tj. zmiany infinitezymalnej W x), wówczas obliczenie nachylenia zbliża się coraz bliżej dokładnego nachylenia w punkcie (patrz rysunek po prawej stronie).,
nie wdając się w zbyt skomplikowane szczegóły, Newton (i jego współczesny Gottfried Leibniz niezależnie) obliczył pochodną funkcję f '(x), która daje nachylenie w dowolnym punkcie funkcji f(x). Ten proces obliczania nachylenia lub pochodnej krzywej lub funkcji nazywa się różniczkowaniem lub różniczkowaniem (lub, w terminologii Newtona, „metodą fluxionów – – nazwał chwilową szybkość zmian w określonym punkcie na krzywej „fluxionem”, a zmieniające się wartości x i y”fluentami”)., Na przykład, pochodna prostej typu f (x) = 4x jest tylko 4; pochodna funkcji kwadratowej f(x) = x2 jest 2x; pochodna funkcji sześciennej F(x) = x3 jest 3×2, itd. Uogólniając pochodną dowolnej funkcji potęgowej f (x) = xr jest rxr-1. Inne funkcje pochodne mogą być określone, zgodnie z pewnymi zasadami, dla funkcji wykładniczych i logarytmicznych, funkcji trygonometrycznych, takich jak sin( x), cos (x), itd., tak że funkcja pochodna może być określona dla dowolnej krzywej bez nieciągłości., Na przykład pochodna krzywej f (x) = x4-5×3 + sin(x2) będzie f '(x) = 4×3 – 15×2 + 2xcos (x2).
Po ustaleniu funkcji pochodnej dla danej krzywej łatwo jest obliczyć nachylenie w dowolnym punkcie na tej krzywej, po prostu wstawiając wartość dla x. w przypadku wykresu czasowo-dystansowego, na przykład, nachylenie to reprezentuje prędkość obiektu w danym punkcie.,
metoda Fluentów
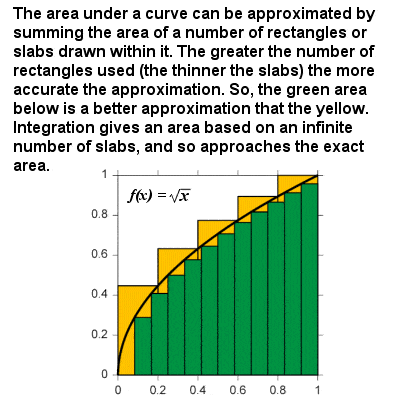
Integracja przybliża obszar pod krzywą, ponieważ wielkość próbek zbliża się do zera
„przeciwieństwem” różnicowania jest całkowanie lub rachunek całkowy (lub, w terminologii Newtona, „metoda fluentów”), i razem różnicowanie i integracja są dwie główne operacje rachunku., Podstawowe twierdzenie Newtona o rachunku różniczkowym mówi, że różnicowanie i całkowanie są operacjami odwrotnymi, tak że jeśli funkcja jest najpierw zintegrowana, a następnie zróżnicowana (lub odwrotnie), oryginalna funkcja jest odzyskiwana.
całkę krzywej można traktować jako wzór do obliczania pola ograniczonego przez krzywą i osi x pomiędzy dwiema zdefiniowanymi granicami. Na przykład na wykresie prędkości względem czasu obszar „pod krzywą” reprezentowałby przebytą odległość., Zasadniczo integracja opiera się na procedurze ograniczającej, która przybliża obszar obszaru krzywoliniowego przez rozbicie go na nieskończenie cienkie pionowe płyty lub kolumny. W ten sam sposób, jak w przypadku różnicowania, Całka może być określona w kategoriach ogólnych: Całka dowolnej potęgi f (x) = xr jest xr+1⁄R + 1, A istnieją inne całki dla funkcji wykładniczych i logarytmicznych, funkcji trygonometrycznych itp., tak że pole pod dowolną krzywą ciągłą można uzyskać między dowolnymi dwoma granicami.,
Newton postanowił nie publikować od razu swojej rewolucyjnej matematyki, obawiając się, że zostanie wyśmiany za swoje niekonwencjonalne pomysły i zadowolił się krążeniem swoich myśli wśród przyjaciół. W końcu miał wiele innych zainteresowań, takich jak filozofia, alchemia i jego praca w Mennicy Królewskiej. Jednak w 1684 roku niemiecki Leibniz opublikował własną, niezależną wersję teorii, podczas gdy Newton nie opublikował nic na ten temat aż do 1693 roku., Chociaż Royal Society, po należytej naradzie, przyznało Newtonowi pierwsze odkrycie (i uznanie za pierwszą publikację Leibnizowi), doszło do pewnego skandalu, gdy upubliczniono, że późniejsze oskarżenie Royal Society o plagiat przeciwko Leibnizowi nie było w rzeczywistości autorstwa żadnego innego Newtona, co wywołało ciągłe kontrowersje, które zniszczyły kariery obu mężczyzn.,
uogólnione twierdzenie dwumianowe
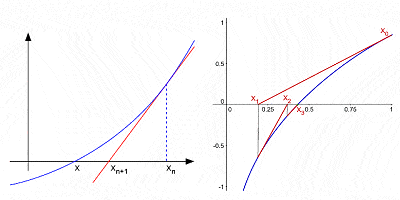
Metoda Newtona do przybliżania korzeni krzywej przez kolejne interwencje po wstępnym odgadnięciu
mimo że jest zdecydowanie najbardziej znanym wkładem w matematykę, rachunek nie był w żaden sposób jedynym wkładem Newtona.,A2 – b2); wniósł znaczący wkład w teorię różnic skończonych (wyrażenia matematyczne w postaci f (x + b) – f(x + a)); był jednym z pierwszych, którzy użyli wykładników ułamkowych i geometrii współrzędnych do wyprowadzenia rozwiązań równań Diofantynowych(równań algebraicznych ze zmiennymi całkowitymi); opracował tzw. „metodę Newtona” do znajdowania kolejno lepszych przybliżeń do zer lub korzeni funkcji; był jednym z pierwszych, którzy pierwszy, aby użyć serii nieskończonej mocy z jakąkolwiek pewnością; itp.,
w 1687 roku Newton opublikował swoją „Principia” lub „The Mathematical Principles of Natural Philosophy”, powszechnie uznawaną za największą książkę naukową, jaką kiedykolwiek napisano. Przedstawił w nim swoje teorie ruchu, grawitacji i mechaniki, wyjaśnił ekscentryczne orbity komet, pływy i ich odmiany, precesję osi Ziemi i ruch Księżyca.,
w późniejszym okresie życia napisał wiele traktatów religijnych zajmujących się dosłowną interpretacją Biblii, poświęcił wiele czasu alchemii, przez kilka lat pełnił funkcję posła do parlamentu, a w 1699 roku został być może najbardziej znanym mistrzem Mennicy Królewskiej, którą piastował aż do śmierci w 1727 roku. W 1703 został prezesem Royal Society, a w 1705 został pierwszym naukowcem, który otrzymał tytuł szlachecki. Zatrucie rtęcią z powodu jego alchemicznych poszukiwań może tłumaczyć ekscentryczność Newtona w późniejszym życiu, a być może także jego ostateczną śmierć.,
| << Back to Pascal | Forward to Leibniz >> |
Leave a Reply