Radianer & DegreesReducing AnglesReference Vinkler
Purplemath
I forrige avsnitt, finner vi den første sirkelen vinkel-ekvivalenter for gitt vinkel tiltak. En annen ting vi kan gjøre med vinkel tiltak, selv de som tiltak er i første go-around, er å finne hva som er kalt «referanse» vinkel.
referanse vinkel er vinkelen som en gitt vinkel gjør med x-aksen., Uavhengig av hvor vinkelen ender (som er, uavhengig av plasseringen av terminalen siden av vinkel), referanse vinkel måler nærmeste avstand av at terminalen side til x-aksen.
Innhold Fortsetter Under
MathHelp.,com

Når du å finne referanse vinkler, kan det være nyttig å huske på at den positive x-aksen er 0° (og 360° eller 0 radianer (og 2π radianer); den positive y-aksen er 90° eller
radianer; den negative x-aksen er 180° eller π radianer, og den negative y-aksen er 270 grader eller radianer.
La oss komme i gang med et enkelt eksempel., Vinkelen med mål 30° ville grafen som dette:
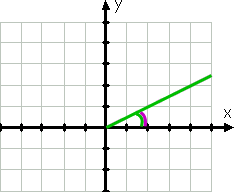
For graftegning, vinkelen er første side er den positive x-aksen, sin terminal side er den grønne linjen, fordi vinkler er trukket går mot klokken. Den buede grønn linje viser en gitt vinkel.
Selv før du har tegning vinkel, jeg vil ha visst at vinkelen er i første kvadrant fordi 30° er mellom 0° og 90°. Referanse vinkel, som vist ved den buede lilla linje, er det samme som en gitt vinkel.,
vinkelen 150°, selvsagt, er ikke det samme som vinkelen 30°; det er større og sin terminal-siden er i den andre kvadranten (fordi 150° er mellom 90° og 180°). Imidlertid, at terminalen siden er bare 30° fra den negative x-aksen, som du kan se av den lilla linjen i tegning:
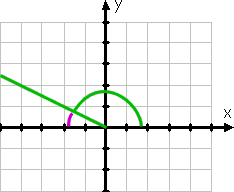
Siden terminalen siden av 150° er bare tretti grader fra den (negative) x-aksen (blir tretti grader mindre enn 180°, som er den negative x-aksen), deretter referanse vinkel (igjen vist ved den buede lilla linje) er 30°.,
du Fortsetter rundt mot klokka, vi kan tegne grafen 210°. Denne vinkelen er terminal siden, fordi 210° er mellom 180° og 270°, er i tredje kvadrant, og denne siden er nærmest til den negative x-aksen. Fordi 210 tretti mer enn 180, så denne vinkelen s terminal (side 30° fortiden (som nedenfor) den negative x-aksen.
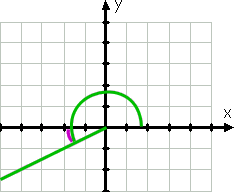
Derfor, referanse-vinkel er, igjen, 30°.
jeg vedder på at du kan gjette hva som ville være referanse vinkel for 330°., Siden 330 er tretti mindre enn 360, og siden 360° = 0°, da vinkelen 330° er tretti grader under (som er, kort av) den positive x-aksen, i fjerde kvadrant. Så dens referanse vinkel på 30°.
Affiliate
Affiliate –
– >

legg Merke til hvordan denne siste beregning var gjort. Jeg hadde ikke en graf. Jeg bare gjorde det aritmetiske i mitt hode. Du skal tegne grafer for så lenge du trenger hjelp, men ikke vær redd for å begynne å stole på matematikk., Når du får taket på dette, det er egentlig ganske grei.
Merk: Fordi referanse vinkel alltid måler (positiv) avstanden fra x-aksen, det kan også bli sett på som å være den første kvadrant tilsvarende vinkel. Med andre ord, for hver av eksemplene ovenfor, hvis min lærebok definert «referanse vinkel» som «den første kvadrant vinkel med den samme avstanden fra x-aksen», så den lilla «referanse vinkel» line (den buede lilla linje, pluss en terminal (side) ville ha blitt trukket i første kvadrant.
uansett, verdien for referanse vinkel vil alltid være den samme., Men hvis du er pålagt å tegne et bilde som viser referanse vinkel, sørg for at du tegner det på den plasseringen som er ansett som «riktig» for din klasse.
-
Finn referansen vinkel for 1500°.
jeg vil ta min kalkulator og gjøre delingen av 360° for «en gang rundt»:
1500 ÷ 360 = 4.16666…
Så det er fire sykluser, pluss litt. Hvor mye er bare fire sykluser?
4 × 360 = 1440
Det betyr at venstre-over-delen (den 0.16666… ovenfor) representerer en annen seksti grader., Dette er mindre enn nitti grader, så terminalen siden av vinkelen er til høyre for den positive y-aksen. Deretter referanse vinkel er i første kvadrant og er lik:
60°
Innhold Fortsetter Under
-
Finn den første kvadrant referanse vinkel for 954°, og trekke begge vinkler på samme akse system.
jeg vil starte med å redusere denne vinkelen. Hvor mange sykluser som passer i denne vinkelen?
954 ÷ 360 = 2.65
To sykluser passer inn i vinkelen., Hvor mye av vinkelen er måle gjøre de to sykluser ta opp?
360 × 2 = 720
Så hvor mye som er igjen?
954 – 720 = 234
Den negative x-aksen er 180°, og den negative y-aksen er 270°. Denne vinkelen er mellom disse verdiene, så det er i tredje kvadrant, og vil være nærmest til den negative x-aksen.
Hvordan du i nærheten? Det vil være avstand mellom terminal side av redusert vinkel og den negative x-aksen:
234 – 180 = 54
Så referanse vinkel er:
54°
…,og tegningen er:
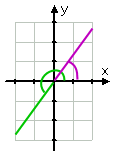
Affiliate
legg Merke til hvordan jeg trakk redusert vinkel (som er den opprinnelige vinkelen, mindre to sykluser) i grønt, og da jeg trakk den første kvadrant referanse vinkel i lilla. Når du gjør tegninger som inneholder to (eller flere) forskjellige biter av informasjon, kan det være nyttig å ha fargeblyanter på hånden. Ja, jeg brukte fargeblyanter på college.
-
Finn referansen vinkel for radianer.,
Annonsering
Ok, dette er i radianer. Så jeg trenger for å tenke i form av 0 radianer og 2π radianer for den positive x-aksen, og π radianer for den negative x-aksen.
vinkelen de har gitt meg er
radianer. Gjør divisjon for å konvertere brøk skjemaet for å desimal form (og ignorerer π for øyeblikket), får jeg:
16 ÷ 5 = 3.2
med andre ord,
radianer er lik 3.2 π radianer. En syklus er 2π radianer, så dette er litt mer enn halv gang så mye som en syklus., Med andre ord, denne vinkelen går litt forbi den negative x-aksen:
3.2 π – 2π = 1.2 π
Men hvor langt er terminal side fra den negative x-aksen?
jeg kan finne ut av dette ved å trekke fra den vinkelen måle i den negative x-aksen redusert fra min vinkel:
1.2 π – 1π
– >
= 0.2 π
= (1/5)π
Dette gir meg avstand mellom terminal siden av (redusert) vinkel og den (negative) x-aksen i radianer. Referanse vinkel er:
-
Finn referansen vinkel for radianer.,
Siden
er mindre enn 2, men mer enn det , så er denne vinkelen er i fjerde kvadranten, mellom radianer og 2π radianer. Da er det nærmeste til den positive x-aksen. Men hvordan i nærheten? Jeg vil trekke fra for å finne ut:
Så referanse vinkel er:
Enten du jobber i grader eller radianer, så lenge du kjenner vinkelen tiltak for positive og negative deler av x-aksen, kan du redusere vinkel (hvis nødvendig), og deretter gjøre subtractions for å få referansen vinkel., Hvis du ikke er sikker på arbeidet ditt, kan du tegne bildet for å være sikker. Men hvis du fortsatt trenger for å tegne bilder når testen kommer opp, kan du prøve å gjøre litt ekstra praksis, fordi testen kommer til å anta at du ikke trenger tid til å tegne bilder.
Du kan bruke Mathway widget nedenfor til å øve på å finne medianen. Prøv angitt trening, eller skriv inn i din egen trening. Deretter klikker du på knappen og velg «Finn Referanse Vinkel» å sammenligne dine svar til Mathway er.,
Vennligst godta «preferences» informasjonskapsler for å aktivere denne widgeten.
(Klikk på «Hurtig på for å vise fremgangsmåten for» å bli tatt direkte til Mathway stedet for en betalt oppgradere.)
URL: https://www.purplemath.com/modules/radians3.htm
Side 1Page 2Page 3
Leave a Reply