
통계는 배열의 통계적 테스트 분석가들이 사용을 추론에서 데이터를 주어집니다. 이러한 테스트를 통해 데이터에서 관찰 된 패턴을 기반으로 결정을 내릴 수 있습니다. 넓은 범위가 있습니다.통계 테스트. 활용할 통계 테스트의 선택은 데이터의 구조,데이터의 분포 및 변수 유형에 의존합니다.,통계에는 t-test,Z-test,chi-square test,anova test,binomial test,one sample median test 등과 같은 다양한 유형의 테스트가 있습니다.
통계 테스트 선택-
데이터가 정상적으로 분산 된 경우 파라 메트릭 테스트가 사용됩니다.파라 메트릭 통계 테스트는 모집단 매개 변수와 데이터가 온 분포에 대한 가정을합니다. 이러한 유형의 테스트를 포함 t-테스트,z-테스트 및 분산 분석 테스트는 가정 데이터에서는 정상 유통.,
Z-test-A z-test 는 분산이 알려지고 표본 크기가 클 때 두 모집단 수단이 다른지 여부를 결정하는 데 사용되는 통계 테스트입니다. Z 에서-모집단의 테스트 평균이 비교됩니다.사용 된 매개 변수는 모집단 평균 및 모집단 표준 편차입니다. Z-test 는 그려진 샘플이 동일한 모집단에 속한다는 가설을 검증하는 데 사용됩니다.,
호:샘플을 의미가 동일한으로 모집단 평균(Null 가설)
Ha:샘플을 의미하지 않으로 동일 인구균(다른 가설)
z=(x—μ)/(σ/√n)
,x=샘플을 의미,u=인구균,σ/√n=인구는 표준 편차가 있다고 가정합니다.
z 값이 임계 값보다 작 으면 귀무 가설을 받아들이십시오.
T-test-t-test 에서 주어진 두 샘플의 평균이 비교됩니다. T-테스트는 모집단 매개 변수(평균 및 표준 편차)가 알려지지 않은 경우에 사용됩니다.,
짝을 이루는 T-Test-동일한 모집단(사전 및 사후 테스트 점수)에서 두 변수의 차이에 대한 테스트. 예를 들어-프로그램 완료 전후의 연수생의 교육 프로그램 성과 점수에서.
독립 T-테스트-independent t-test 또는 sample t-test 또는 학생의 t-테스트,통계적 테스트는지 여부를 결정하는가 통계적으로 유의한 차이를 의미에서 두 개의 관련이 없는 그룹이다.예를 들어-인구의 소년과 소녀 비교.,
하나의 샘플 t-테스트-단일 그룹의 평균은 주어진 평균과 비교됩니다. 예를 들어-평균 판매가 주어지면 매출의 증가 및 감소를 확인합니다.
t=(x1—x2)/(σ/√n1+σ/√n2),
여기서 x1 과 x2 는 각각 샘플 1 과 샘플 2 의 평균이다.
ANOVA Test-분산 분석(ANOVA)은 두 개 이상의 그룹의 수단이 서로 크게 다른지 확인하는 데 사용되는 통계 기법입니다. ANOVA 는 다른 샘플의 수단을 비교하여 하나 이상의 요인의 영향을 확인합니다., ANOVA 테스트 대신 t-테스트를 사용하면 샘플 수가 2 개 이상이므로 신뢰할 수 없으며 결과에 오류가 발생합니다.
분산 분석에서 테스트되는 가설은
Ho:모든 샘플 쌍은 동일합니다., 모든 샘플을 의미가 동일
Ha:적어도 한 쌍의 샘플 크게 다르
에 분산 분석 테스트는 우리가 계산 F 값과 비교 중요한 가치
F=((SSE1—SSE2)/m)/SSE2/n-k, where
SSE=잔류 제곱
m=의 수를 제한을
k=숫자의 독립적인 변수를
비수 통계적 테스트-금 파라미터를 테스트할 때 사용되는 데이터가 정상적으로 배포됩니다. 비 파라 메트릭 테스트에는 카이 제곱 테스트가 포함됩니다.
Chi-square test(χ2test)-chi-square test 는 두 범주 형 변수를 비교하는 데 사용됩니다., 계산 Chi-Square 통계 값과 비교에 대한 중요한 가치로서 Chi-Square 배포할 수 있는지 평가하는 관찰된 주파수에 크게 다르에서 예상되는 주파수입니다.
카이 제곱에 대해 테스트중인 가설은-
Ho:변수 x 와 변수 y 는 독립적입니다
Ha:변수 x 와 변수 y 는 독립적이지 않습니다.,
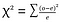
where o=observed , e=expected.
Leave a Reply