Radianti & DegreesReducing AnglesReference Angoli
Purplemath
Nella sezione precedente, abbiamo trovato il primo cerchio angolo equivalenti per un dato angolo di misure. Un’altra cosa che possiamo fare con le misure angolari, anche quelle le cui misure sono nel primo go-around, è trovare quello che viene chiamato l’angolo di” riferimento”.
L’angolo di riferimento è l’angolo che l’angolo dato fa con l’asse X., Indipendentemente da dove finisce l’angolo (cioè, indipendentemente dalla posizione del lato terminale dell’angolo), l’angolo di riferimento misura la distanza più vicina di quel lato terminale all’asse X.
Il contenuto continua sotto
MathHelp.,com

Durante la ricerca di riferimento angoli, può essere utile tenere a mente che il positivo dell’asse x è 0° (360° o 0 radianti (2π radianti); l’asse y positivo è di 90° o
radianti; l’asse x negativo è di 180° o π radianti; e l’asse y negativo è di 270° o radianti.
Iniziamo con un semplice esempio., L’angolo con misura 30 ° sarebbe grafico come questo:
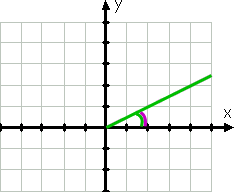
Per la grafica, il lato iniziale dell’angolo è l’asse x positivo; il suo lato terminale è la linea verde, perché gli angoli sono disegnati in senso antiorario. La linea verde curva mostra l’angolo dato.
Anche prima di aver disegnato l’angolo, avrei saputo che l’angolo è nel primo quadrante perché 30° è tra 0° e 90°. L’angolo di riferimento, mostrato dalla linea viola curva, è lo stesso dell’angolo dato.,
L’angolo 150°, ovviamente, non è lo stesso dell’angolo 30°; è più grande e il suo lato terminale è nel secondo quadrante (perché 150° è tra 90° e 180°). Tuttavia, quel lato terminale è solo 30° dall’asse x negativo, come si può vedere dalla linea viola nel disegno:
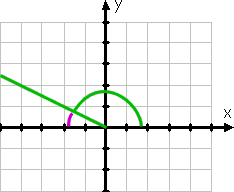
Poiché il lato terminale del 150° è solo trenta gradi dall’asse x (negativo) (essendo trenta gradi meno di 180°, che è l’asse x negativo), allora l’angolo di riferimento (di nuovo mostrato dalla linea viola curva) è 30°.,
Continuando in senso antiorario, possiamo rappresentare graficamente 210°. Il lato terminale di questo angolo, poiché 210 ° è compreso tra 180° e 270°, si trova nel terzo quadrante e questo lato è più vicino all’asse x negativo. Poiché 210 è trenta più di 180, allora il lato terminale di questo angolo è 30 ° oltre (cioè sotto) l’asse x negativo.
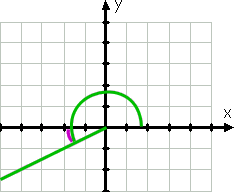
Pertanto, l’angolo di riferimento è, ancora una volta, di 30°.
Scommetto che puoi indovinare quale sarebbe l’angolo di riferimento per 330°., Poiché 330 è trenta meno di 360, e poiché 360 ° = 0°, allora l’angolo 330° è trenta gradi sotto (cioè, a corto di) l’asse x positivo, nel quarto quadrante. Quindi il suo angolo di riferimento è 30°.
Affiliate
Affiliate

Si noti come è stato eseguito questo ultimo calcolo. Non avevo un grafico. Ho appena fatto l’aritmetica nella mia testa. Dovresti disegnare grafici per tutto il tempo necessario, ma non aver paura di iniziare a fare affidamento sull’aritmetica., Una volta capito, è davvero molto semplice.
Nota: Poiché l’angolo di riferimento misura sempre la distanza (positiva) dall’asse x, può anche essere visto come l’angolo equivalente del primo quadrante. In altre parole, per ciascuno degli esempi sopra, se il mio libro di testo definisse “angolo di riferimento” come “l’angolo del primo quadrante con la stessa distanza dall’asse x”, allora la linea viola “angolo di riferimento” (la linea viola curva, più un lato terminale) sarebbe stata disegnata nel primo quadrante.
In entrambi i casi, il valore per l’angolo di riferimento sarà sempre lo stesso., Ma se ti viene richiesto di disegnare un’immagine che mostri l’angolo di riferimento, assicurati di disegnarla nella posizione considerata “corretta” per la tua classe.
-
Trovare l’angolo di riferimento per 1500°.
Prendo la mia calcolatrice e faccio la divisione di 360° per “una volta intorno”:
1500 ÷ 360 = 4.16666…
Quindi ci sono quattro cicli, più un po’. Quanto costa solo i quattro cicli?
4 × 360 = 1440
Ciò significa che la parte sinistra-over (il 0.16666… sopra) rappresenta altri sessanta gradi., Questo è più piccolo di novanta gradi, quindi il lato terminale dell’angolo è a destra dell’asse y positivo. Quindi l’angolo di riferimento è nel primo quadrante ed è uguale a:
60°
Il contenuto Continua sotto
-
Trova l’angolo di riferimento del primo quadrante per 954° e disegna entrambi gli angoli sullo stesso sistema di assi.
Inizierò riducendo questo angolo. Quanti cicli rientrano in questo angolo?
954 ÷ 360 = 2.65
Due cicli si adattano all’angolo., Quanto della misura dell’angolo occupano questi due cicli?
360 × 2 = 720
Allora quanto rimane?
954-720 = 234
L’asse x negativo è 180° e l’asse y negativo è 270°. Questo angolo è tra questi valori, quindi è nel terzo quadrante e sarà più vicino all’asse x negativo.
Quanto vicino? Sarà la distanza tra il lato terminale dell’angolo ridotto e l’asse x negativo:
234 – 180 = 54
Quindi l’angolo di riferimento è:
54°
…,e il disegno è:
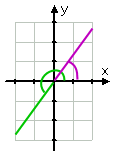
Affiliato
si Noti come l’ho disegnato il ridotto angolo (essendo l’angolo originale, meno di due cicli) in verde, e poi ho disegnato il primo quadrante angolo di riferimento in viola. Quando stai facendo disegni che contengono due (o più) pezzi distinti di informazioni, può essere utile avere matite colorate a portata di mano. Sì, ho usato matite colorate al college.
-
Trova l’angolo di riferimento per i radianti.,
Pubblicità
Va bene, questo è in radianti. Quindi dovrò pensare in termini di 0 radianti e 2π radianti per l’asse x positivo, e π radianti per l’asse x negativo.
L’angolo che mi hanno dato è
radianti. Facendo la divisione per convertire la forma frazionaria in forma decimale (e ignorando il π per il momento), ottengo:
16 ÷ 5 = 3.2
In altre parole,
radianti è uguale a 3.2 π radianti. Un ciclo è 2π radianti, quindi questo è un po ‘ più della metà-di nuovo tanto quanto un ciclo., In altre parole, questo angolo va un po ‘ oltre l’asse x negativo:
3.2 π-2π = 1.2 π
Ma quanto è lontano il lato terminale dall’asse x negativo?
posso capire questo, sottraendo l’angolo di misura dell’asse x negativo dal mio angolo ridotto:
1.2 π – 1 π
= 0.2 π
= (1/5)π
Questo mi dà la distanza tra il terminale lato (ridotto) angolo e il (negativo) dell’asse x in radianti. L’angolo di riferimento è:
-
Trova l’angolo di riferimento per i radianti.,
Poiché
è inferiore a 2 ma più di , allora questo angolo è nel quarto quadrante, tra radianti e radianti 2π. Quindi è più vicino all’asse x positivo. Ma quanto vicino? Sottraggo per scoprire:
Quindi l’angolo di riferimento è:
Se stai lavorando in gradi o in radianti, finché conosci le misure dell’angolo per le porzioni positive e negative dell’asse x, puoi ridurre l’angolo (se necessario) e quindi fare sottrazioni per ottenere l’angolo di riferimento., Se non sei sicuro del tuo lavoro, puoi disegnare l’immagine per essere sicuro. Ma se hai ancora bisogno di disegnare immagini quando il test sta arrivando, prova a fare un po ‘ di pratica in più, perché il test assumerà che non hai bisogno del tempo per disegnare le immagini.
Puoi usare il widget Mathway qui sotto per esercitarti a trovare la mediana. Prova l’esercizio inserito o digita il tuo esercizio. Quindi fai clic sul pulsante e seleziona “Trova l’angolo di riferimento” per confrontare la tua risposta con quella di Mathway.,
Per abilitare questo widget, ti preghiamo di accettare i cookie “preferenze”.
(Fare clic su “Toccare per visualizzare i passaggi” da prendere direttamente al sito Mathway per un aggiornamento a pagamento.)
URL: https://www.purplemath.com/modules/radians3.htm
Pagina 1Page 2Page 3
Leave a Reply