Radians & DegreesReducing AnglesReference Angles
Purplemath
dans la section précédente, nous avons trouvé les équivalents d’angle du premier cercle pour des mesures d’angle données. Une autre chose que nous pouvons faire avec les mesures d’angle, même celles dont les mesures sont dans la première remise des gaz, est de trouver ce qu’on appelle l’angle « de référence ».
L’angle de référence est l’angle que l’angle avec l’axe des abscisses., Quel que soit l’endroit où l’angle se termine (c’est-à-dire quel que soit l’emplacement du côté terminal de l’angle), l’angle de référence mesure la distance la plus proche de ce côté terminal de l’axe des abscisses.
Contenu Continue ci-Dessous
MathHelp.,com

lors de la recherche d’angles de référence, il peut être utile de garder à l’esprit que l’axe X positif est 0° (et 360° ou 0 radians (et 2π radians); l’axe 90° ou
radians; l’axe X négatif est 180° ou π radians; et l’axe Y négatif est 270° ou radians.
commençons par un exemple simple., L’angle avec la mesure 30° serait graphique comme ceci:
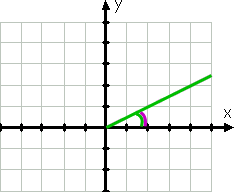
pour le graphique, le côté initial de l’angle est l’axe X positif; son côté terminal est la ligne verte, car les angles sont dessinés dans le sens antihoraire. La ligne verte courbe montre l’angle donné.
avant même d’avoir dessiné l’angle, j’aurais su que l’angle est dans le premier quadrant car 30° est compris entre 0° et 90°. L’angle de référence, représenté par la ligne violette incurvée, est le même que l’angle donné.,
l’angle 150°, évidemment, n’est pas le même que l’angle 30°; il est plus grand, et son côté terminal est dans le deuxième quadrant (car 150° est compris entre 90° et 180°). Cependant, ce côté terminal n’est qu’à 30° de l’axe X négatif, comme vous pouvez le voir par la ligne violette sur le dessin:
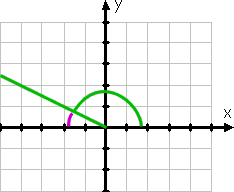
puisque le côté terminal du 150° n’est qu’à trente degrés de l’axe x (négatif) (étant de trente degrés inférieur à 180°, qui est l’axe X négatif), alors l’angle de référence (encore représenté par la ligne violette incurvée) est de 30°.,
en continuant dans le sens inverse des aiguilles d’une montre, nous pouvons représenter 210°. Le côté terminal de cet angle, parce que 210° est entre 180° et 270°, est dans le troisième quadrant, et ce côté est le plus proche de l’axe des abscisses négatif. Parce que 210 est trente de plus que 180, alors le côté terminal de cet angle est 30° au-delà (c’est-à-dire en dessous) de l’axe des abscisses négatif.
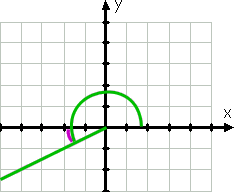
par conséquent, l’angle de référence est, à nouveau, de 30°.
je parie que vous pouvez deviner quel serait l’angle de référence pour 330°., Puisque 330 est trente moins que 360, et puisque 360° = 0°, alors l’angle 330° est trente degrés en dessous (c’est-à-dire en deçà de) l’axe des abscisses positif, dans le quatrième quadrant. Son angle de référence est donc de 30°.
d’Affiliation
d’Affiliation

Remarquez comment ce dernier calcul a été fait. Je n’ai pas de graphique. Je viens de faire l’arithmétique dans ma tête. Vous devriez dessiner des graphiques aussi longtemps que vous en avez besoin, mais n’ayez pas peur de commencer à vous fier à l’arithmétique., Une fois que vous obtenez le coup de cela, c’est vraiment assez simple.
Remarque: Étant donné que l’angle de référence mesure toujours la distance (positive) par rapport à l’axe des abscisses, il peut également être considéré comme étant l’angle équivalent du premier quadrant. En d’autres termes, pour chacun des exemples ci-dessus, si mon manuel définissait « angle de référence » comme « l’angle du premier quadrant avec la même distance de l’axe des x », alors la ligne « angle de référence » violette (la ligne violette incurvée, plus un côté terminal) aurait été dessinée dans le premier quadrant.
de toute façon, la valeur de l’angle de référence sera toujours le même., Mais si vous devez dessiner une image montrant l’angle de référence, assurez-vous de la dessiner à l’endroit considéré comme « correct » pour votre classe.
-
Trouver l’angle de référence pour 1500°.
je vais prendre ma calculatrice et faire la division par 360° pour le « tour »:
1500 ÷ 360 = 4.16666…
il y a Donc quatre cycles, plus un peu. Combien coûte juste les quatre cycles?
4 × 360 = 1440
cela signifie Que l’excédent de la partie (le 0.16666… ci-dessus) représente encore soixante degrés., Ceci est inférieur à quatre-vingt-dix degrés, de sorte que le côté terminal de l’angle est à droite de l’axe Y positif. Ensuite, l’angle de référence est dans le premier quadrant et est égale à:
60°
le Contenu Continue ci-Dessous
-
Trouver le premier quadrant angle de référence pour 954°, et de dessiner les deux angles sur l’axe même du système.
je vais commencer par réduire cet angle. Combien de cycles correspondent à cet angle?
954 ÷ 360 = 2.65
Deux cycles d’ajustement à l’intérieur de l’angle., Combien de la mesure de l’angle ces deux cycles prennent-ils?
360 × 2 = 720
Ensuite, combien?
954 – 720 = 234
l’axe X négatif est de 180° et l’axe y négatif est de 270°. Cet angle est entre ces valeurs, il est donc dans le troisième quadrant, et sera le plus proche de l’axe des abscisses négatif.
Comment fermer? Ça va être la distance entre le côté terminal d’un angle réduit et le négatif de l’axe des x:
234 – 180 = 54
Ensuite, l’angle de référence est:
54°
…,et le dessin est:
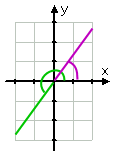
d’Affiliation
vous remarquerez que j’ai attiré l’angle réduit (soit l’angle original, moins deux cycles) en vert, puis j’ai dessiné le premier quadrant angle de référence en violet. Lorsque vous faites des dessins qui contiennent deux (ou plus) informations distinctes, il peut être utile d’avoir des crayons de couleur à portée de main. Oui, j’ai utilisé des crayons de couleur à l’Université.
-
trouver l’angle de référence pour les radians.,
Publicité
d’Accord, c’est en radians. Je devrai donc penser en termes de 0 radians et 2π radians pour l’axe X positif, et π radians pour l’axe X négatif.
L’angle qu’ils m’ont donné est
radians. En faisant la division pour convertir la forme fractionnaire en forme décimale (et en ignorant le π pour le moment), j’obtiens:
16 ÷ 5 = 3.2
En d’autres termes,
radians est égal à 3.2 π radians. Un cycle est 2π radians, donc c’est un peu plus de la moitié de nouveau autant qu’un cycle., En d’autres termes, cet angle va un peu au-delà de l’axe X négatif:
3.2 π – 2π = 1.2 π
Mais à quelle distance est le côté terminal de l’axe X négatif?
je ne peux comprendre cela en soustrayant la mesure d’angle de l’axe x négatif de mon angle réduit:
1.2 π – 1π
= 0.2 π
= (1/5)π
Cela me donne la distance entre le côté terminal de l’ (réduit) l’angle et l’ (négatif) de l’axe des x en radians. L’angle de référence est:
-
Trouver la référence de l’angle en radians.,
Depuis
est inférieur à 2, mais en plus , alors cet angle est dans le quatrième quadrant, entre radians et 2π radians. Ensuite, il est le plus proche de l’axe des abscisses positif. Mais comment? Je vais soustraire pour savoir:
alors l’angle de référence est:
que vous travailliez en degrés ou en radians, tant que vous connaissez les mesures d’angle pour les parties positives et négatives de l’axe des x, vous pouvez réduire l’angle (si nécessaire), puis faire des soustractions pour obtenir, Si vous n’êtes pas sûr de votre travail, vous pouvez dessiner l’image pour être sûr. Mais si vous avez encore besoin de dessiner des images lorsque le test est à venir, essayez de faire une pratique supplémentaire, car le test va supposer que vous n’avez pas besoin de temps pour dessiner les images.
Vous pouvez utiliser le widget Mathway ci-dessous pour vous entraîner à trouver la médiane. Essayez l’exercice entré, ou tapez votre propre exercice. Cliquez ensuite sur le bouton et sélectionnez « trouver L’Angle de référence » pour comparer votre réponse à celle de Mathway.,
Veuillez accepter « préférences » cookies afin de permettre à ce widget.
(Cliquez sur « Appuyez pour afficher les étapes » à effectuer directement sur le site Mathway pour une mise à niveau payante.)
URL: https://www.purplemath.com/modules/radians3.htm
Page 1Page 2Page 3
Leave a Reply