radianes & DegreesReducing AnglesReference Angles
Purplemath
en la sección anterior, encontramos los equivalentes de ángulo del primer círculo para medidas de ángulo dadas. Otra cosa que podemos hacer con las medidas de ángulo, incluso aquellas cuyas medidas están en la primera vuelta, es encontrar lo que se llama el ángulo de «referencia».
el ángulo de referencia es el ángulo que el ángulo dado hace con el eje X., Independientemente de dónde termina el ángulo (es decir, independientemente de la ubicación del lado terminal del ángulo), el ángulo de referencia mide la distancia más cercana de ese lado terminal al eje X.
Contenido Sigue a Continuación
MathHelp.,com

al Encontrar ángulos de referencia, puede ser útil tener en cuenta que el eje X positivo es 0° (y 360° o 0 radianes 90° o
radianes; el eje x negativo es 180° o π radianes; y el eje y negativo es 270° o radianes.
comencemos con un ejemplo sencillo., El ángulo con la medida 30° se graficaría así:
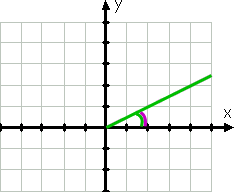
para graficar, el lado inicial del ángulo es el eje X positivo; su lado terminal es la línea verde, porque los ángulos se dibujan en sentido contrario a las agujas del reloj. La línea verde curva muestra el ángulo dado.
incluso antes de haber dibujado el ángulo, habría sabido que el ángulo está en el primer cuadrante porque 30° está entre 0° y 90°. El ángulo de referencia, mostrado por la línea púrpura curvada, es el mismo que el ángulo dado.,
El Ángulo 150°, obviamente, no es el mismo que el ángulo 30°; es más grande, y su lado terminal está en el segundo cuadrante (porque 150° está entre 90° y 180°). Sin embargo, ese lado terminal está a solo 30° del eje x negativo, como se puede ver por la línea púrpura en el dibujo:
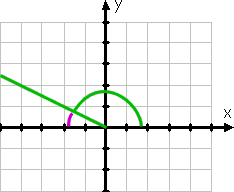
dado que el lado terminal de los 150° está a solo treinta grados del eje x (negativo) (siendo treinta grados menos de 180°, que es el eje x negativo), entonces el ángulo de referencia (nuevamente mostrado por la línea púrpura curva) es 30°.,
continuando en sentido contrario a las agujas del reloj, podemos graficar 210°. El lado terminal de este ángulo, porque 210° está entre 180° y 270°, está en el tercer cuadrante, y este lado está más cerca del eje x negativo. Debido a que 210 es treinta más que 180, entonces el lado terminal de este ángulo está 30° más allá (es decir, debajo) del eje x negativo.
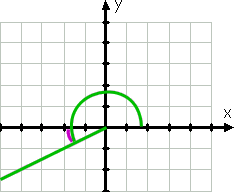
por lo tanto, el ángulo de referencia es, de nuevo, 30°.
apuesto a que puedes adivinar cuál sería el ángulo de referencia para 330°., Dado que 330 es treinta menos que 360, y desde 360° = 0°, entonces el ángulo 330° es treinta grados por debajo (es decir, por debajo de) el eje X positivo, en el cuarto cuadrante. Así que su ángulo de referencia es de 30°.
Afiliados
Afiliados

Observe cómo este último cálculo se ha hecho. No tenía un gráfico. Acabo de hacer la aritmética en mi cabeza. Debe dibujar gráficos durante el tiempo que necesite la ayuda, pero no tenga miedo de comenzar a confiar en la aritmética., Una vez que te acostumbras a esto, es muy sencillo.
Nota: Debido a que el ángulo de referencia siempre mide la distancia (positiva) desde el eje x, también se puede ver como el ángulo equivalente del primer cuadrante. En otras palabras, para cada uno de los ejemplos anteriores, si mi libro de texto define «ángulo de referencia» como «el ángulo del primer cuadrante con la misma distancia desde el eje x», entonces la línea púrpura «ángulo de referencia» (la línea púrpura curvada, más un lado terminal) se habría dibujado en el primer cuadrante.
de cualquier manera, el valor para el ángulo de referencia siempre será el mismo., Pero si se le requiere que dibuje un dibujo que muestre el ángulo de referencia, asegúrese de dibujarlo en la ubicación que se considere «correcta» para su clase.
-
encuentre el ángulo de referencia para 1500°.
tomaré mi calculadora y haré la división por 360° para «once around»:
1500 ÷ 360 = 4.16666…
así que hay cuatro ciclos, más un poco. ¿Cuánto es sólo los cuatro ciclos?
4 × 360 = 1440
eso significa que la porción sobrante (el 0.16666… arriba) representa otros sesenta grados., Esto es más pequeño que noventa grados, por lo que el lado terminal del ángulo está a la derecha del eje y positivo. A continuación, el ángulo de referencia está en el primer cuadrante y es igual a:
60°
Contenido Sigue a Continuación
-
Encontrar el primer cuadrante del ángulo de referencia para 954°, y dibujar ángulos en el mismo eje del sistema.
empezaré por reducir este ángulo. ¿Cuántos ciclos caben dentro de este ángulo?
954 ÷ 360 = 2.65
Dos ciclos de ajuste en el ángulo., ¿Cuánto de la medida del ángulo ocupan esos dos ciclos?
360 × 2 = 720
Entonces, ¿cuánto queda?
954 – 720 = 234
el eje x negativo es 180°, y el eje y negativo es 270°. Este ángulo está entre esos valores, por lo que está en el tercer cuadrante, y será más cercano al eje x negativo.
¿Qué tan cerca? Va a ser la distancia entre el lado terminal del ángulo reducido, en el sentido negativo del eje x:
234 – 180 = 54
a Continuación, el ángulo de referencia es:
54°
…,y el dibujo es:
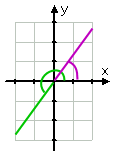
Afiliados
Observe cómo me atrajo el ángulo reducido (siendo el ángulo original, menos dos ciclos) en verde, y entonces me llamó el primer cuadrante del ángulo de referencia en color morado. Cuando hagas dibujos que contengan dos (o más) piezas de información distintas, puede ser útil tener lápices de colores a mano. Sí, usé lápices de colores en la Universidad.
-
encuentre el ángulo de referencia para radianes.,
Anuncio
Bueno, esto es en radianes. Así que necesitaré pensar en términos de 0 radianes y 2π radianes para el eje X positivo y π radianes para el eje x negativo.
El ángulo que me han dado es
radianes. Haciendo la división para convertir la forma fraccionaria a forma decimal (e ignorando el π por el momento), obtengo:
16 ÷ 5 = 3.2
En otras palabras,
radianes es igual a 3.2 π radianes. Un ciclo es 2π radianes, por lo que esto es un poco más de la mitad de nuevo tanto como un ciclo., En otras palabras, este ángulo va un poco más allá del eje x negativo:
3.2 π – 2π = 1.2 π
pero ¿a qué distancia está el lado terminal del eje x negativo?
puedo calcular esto restando la medida del ángulo del eje x negativo de mi ángulo reducido:
1.2 π-1π
= 0.2 π
= (1/5)π
esto me da la distancia entre el lado terminal del ángulo (reducido) y el eje x (negativo) en radianes. El ángulo de referencia es:
-
Encontrar el ángulo de referencia para radianes.,
dado que
es menor que 2 pero más que , entonces este ángulo está en el cuarto cuadrante, entre radianes y radianes 2π. Entonces está más cerca del eje X positivo. ¿Pero qué tan cerca? Restaré para averiguar:
entonces el ángulo de referencia es:
ya sea que esté trabajando en grados o en radianes, siempre y cuando sepa que las medidas de ángulo para las porciones positivas y negativas del eje x, puede reducir el ángulo (si es necesario) y luego hacer restas para obtener el ángulo de referencia., Si no está seguro de su trabajo, puede dibujar el cuadro para estar seguro. Pero si todavía necesita dibujar dibujos cuando se acerca el examen, intente hacer un poco de práctica adicional, porque el examen asumirá que no necesita tiempo para dibujar los dibujos.
puede utilizar el widget Mathway a continuación para practicar la búsqueda de la mediana. Pruebe el ejercicio introducido, o escriba su propio ejercicio. Luego haz clic en el botón y selecciona «Encontrar el ángulo de referencia» para comparar tu respuesta con la de Mathway.,
acepte las cookies de «preferencias» para habilitar este widget.
(Haga clic en «Toque para ver los pasos» para ir directamente al sitio de Mathway para una actualización de pago.)
URL: https://www.purplemath.com/modules/radians3.htm
Página 1Page 2Page 3
Leave a Reply