Radiánů & DegreesReducing AnglesReference Úhly,
Purplemath
V předchozí části, jsme našli první-kruh, úhel ekvivalenty pro daný úhel opatření. Další věc, kterou můžeme udělat s úhlovými opatřeními, dokonce i těmi, jejichž opatření jsou v prvním pohybu, je najít to, co se nazývá „referenční“ úhel.
referenční úhel je úhel, který daný úhel dělá s osou x., Bez ohledu na umístění koncové strany úhlu) měří referenční úhel nejbližší vzdálenost této koncové strany k ose x.
obsah pokračuje pod
MathHelp.,com

Při hledání referenční úhly, to může být užitečné mít na paměti, že pozitivní x-osa je 0° (nebo 360° nebo 0 radiánů (a 2π radiánů); pozitivní osa y je 90° nebo
radiány; negativní x-osa je 180° nebo π radiánů; a negativní y-osa je 270°, nebo v radiánech.
začněme snadným příkladem., Úhel se měří 30° by graf, jako je tento:
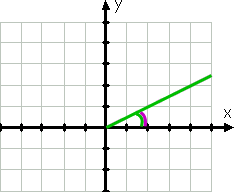
Pro vytváření grafů, úhel počáteční stranu je pozitivní x-osa; jeho terminálu straně je zelená linka, protože úhly jsou vypracovány jít proti směru hodinových ručiček. Zakřivená zelená čára ukazuje daný úhel.
ještě před nakreslením úhlu bych věděl, že úhel je v prvním kvadrantu, protože 30° je mezi 0° a 90°. Referenční úhel, znázorněný zakřivenou fialovou čarou, je stejný jako daný úhel.,
úhel 150°, je zřejmé, že není stejný jako úhel 30°; to je větší a jeho terminálu straně je ve druhém kvadrantu (protože 150° je mezi 90° a 180°). Nicméně, že terminál straně je pouze 30° od negativní x-osa,, jak můžete vidět na fialovou čáru ve výkresu:
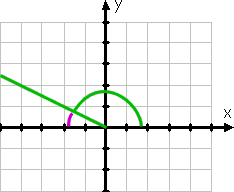
Od terminálu straně 150° je pouze třicet stupňů od (negativních) osa x (třicet stupňů méně než 180°, což je negativní x-osa), pak referenční úhel (opět ukázaly zakřivené fialové linie) je 30°.,
pokračování kolem proti směru hodinových ručiček, můžeme graf 210°. Koncová strana tohoto úhlu, protože 210° je mezi 180° a 270°, je ve třetím kvadrantu a tato strana je nejblíže záporné ose x. Protože 210 je o třicet více než 180, pak je koncová strana tohoto úhlu 30 ° kolem (tj.
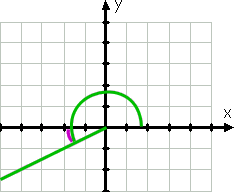
referenční úhel je tedy opět 30°.
vsadím se, že můžete hádat, jaký by byl referenční úhel pro 330°., Vzhledem k tomu, že 330 je třicet méně než 360 a od 360° = 0°, pak je úhel 330° třicet stupňů pod (tj. Takže jeho referenční úhel je 30°.
Affiliate
Affiliate

Všimněte si, jak tento poslední výpočet byl proveden. Neměl jsem graf. Právě jsem udělal aritmetiku v mé hlavě. Měli byste kreslit grafy tak dlouho, jak budete potřebovat pomoc, ale nebojte se začít spoléhat na aritmetiku., Jakmile se dostanete na kloub, je to opravdu docela jednoduché.
poznámka: protože referenční úhel vždy měří (kladnou) vzdálenost od osy x, lze jej také považovat za ekvivalentní úhel prvního kvadrantu. Jinými slovy, pro každý z výše uvedených příkladů, pokud moje učebnice definované „referenční úhel“ jako „první kvadrant úhlu stejné vzdálenosti od osy x“, pak fialové „referenční úhel“ line (zakřivené fialové linky, plus svorka straně) by byly vypracovány v prvním kvadrantu.
ať tak či onak, hodnota referenčního úhlu bude vždy stejná., Pokud však potřebujete nakreslit obrázek zobrazující referenční úhel, ujistěte se, že jej nakreslíte na místě, které je pro vaši třídu považováno za „správné“.
-
Najděte referenční úhel pro 1500°.
vezmu si kalkulačku a udělám rozdělení o 360° pro „jednou kolem“:
1500 ÷ 360 = 4.16666…
takže existují čtyři cykly, plus trochu. Kolik jsou jen čtyři cykly?
4 × 360 = 1440
to znamená, že levá část (0.1666… nahoře) představuje dalších šedesát stupňů., To je menší než devadesát stupňů, takže koncová strana úhlu je vpravo od kladné osy y. Pak referenční úhel je v prvním kvadrantu a se rovná:
60°
Obsah Pokračuje Níže
-
Najít první kvadrant referenční úhel pro 954°, a čerpat oba úhly na stejné ose systému.
začnu snížením tohoto úhlu. Kolik cyklů se vejde do tohoto úhlu?
954 ÷ 360 = 2,65
dva cykly zapadají do úhlu., Kolik z míry úhlu se tyto dva cykly zabírají?
360 × 2 = 720
pak kolik zbývá?
954-720 = 234
záporná osa X je 180° a záporná osa y je 270°. Tento úhel je mezi těmito hodnotami, takže je ve třetím kvadrantu a bude nejblíže záporné ose x.
jak blízko? Bude to vzdálenost mezi svorkou straně snižuje úhel a negativní x-osa:
234 – 180 = 54
Pak úhel odkazu je:
54°
…,a kresba je:
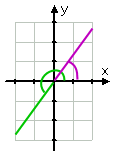
Affiliate
Všimněte si, jak jsem kreslil redukovaný úhel (původní úhel, méně dva cykly) v zelené, a pak jsem nakreslil první kvadrant referenční úhel ve fialové. Když děláte kresby, které obsahují dva (nebo více) odlišné kousky informací, to může být užitečné mít barevné tužky na ruce. Ano, na vysoké jsem použil barevné tužky.
-
Najděte referenční úhel pro radiány.,
reklama
dobře, to je v radiánech. Takže budu muset myslet na 0 radiánů a 2π radiánů pro kladnou osu x a π radiánů pro zápornou osu x.
úhel, který mi dali, je
radián. Dělá rozdělení pro převod zlomkové formě desetinné formě (a ignorování π pro tuto chvíli), dostanu:
16 ÷ 5 = 3.2
jinými slovy,
radiánů se rovná 3.2 π radiánů. Jeden cyklus je 2π radiány, takže je to o něco více než polovina-opět stejně jako jeden cyklus., Jinými slovy, tento úhel jde trochu přes negativní x-osa:
3.2 π – 2π = 1.2 π
Ale jak daleko je terminál straně od negativní x-osa?
vyřeším to tak, že se odečte úhel měření negativní x-osa z mého redukovaný úhel:
1.2 π – 1π
= 0.2 π
= (1/5)π
To mi dává vzdálenost mezi svorkou straně (snížené) úhel a (negativní), osa x je v radiánech. Referenční úhel je:
-
Najděte referenční úhel pro radiány.,
, Protože
je menší než 2, ale více než , pak tento úhel je ve čtvrtém kvadrantu, mezi radiány a 2π radiánů. Pak je nejblíže kladné ose x. Ale jak blízko? Odečtu zjistit:
Pak úhel odkazu je:
Ať už pracujete ve stupních, nebo v radiánech, tak dlouho, jak víte, úhel opatření pro kladné a záporné části osy x, můžete snížit úhel (v případě potřeby), a pak udělat odčítání získat referenční úhel., Pokud si nejste jisti svou prací, můžete obrázek nakreslit, abyste si byli jisti. Ale pokud stále potřebujete kreslit obrázky, když se test blíží, zkuste udělat nějakou další praxi, protože test bude předpokládat, že nepotřebujete čas na kreslení obrázků.
pomocí widgetu Mathway níže můžete procvičit nalezení mediánu. Vyzkoušejte zadané cvičení nebo zadejte své vlastní cvičení. Poté klikněte na tlačítko a vyberte „najít referenční úhel“ porovnat svou odpověď na Mathway je.,
přijměte, Prosím, „předvolby“ cookies aby tento widget.
(klikněte na „Klepnutím zobrazíte kroky“, které chcete provést přímo na web Mathway pro placený upgrade.)
URL: https://www.purplemath.com/modules/radians3.htm
Stránka 1stránky 2Page 3
Leave a Reply