radianer & DegreesReducing AnglesReference Angles
Purplemath
i föregående avsnitt hittade vi de första cirkelvinkelsekvivalenterna för givna vinkelåtgärder. En annan sak vi kan göra med vinkelåtgärder, även de vars åtgärder är i första hand, är att hitta vad som kallas ”referens” – vinkeln.
referensvinkeln är den vinkel som den givna vinkeln gör med X-axeln., Oavsett var vinkeln slutar (det vill säga oberoende av platsen för vinkelns terminalsida) mäter referensvinkeln det närmaste avståndet för den terminalsidan till X-axeln.
innehållet fortsätter under
MathHelp.,com

När du hittar referensvinklar kan det vara bra att komma ihåg att den positiva x-axeln är 0° (och 360° eller 0 radianer (och 2π radianer); den positiva y-axeln är 90° eller
radianer; den negativa X-axeln är 180° eller π radianer; och den negativa y-axeln är 270° eller radianer.
låt oss komma igång med ett enkelt exempel., Vinkeln med mått 30° skulle grafera så här:
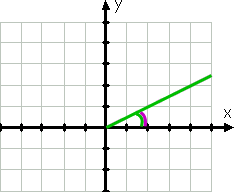
för grafer är vinkelns ursprungliga sida den positiva x-axeln; dess terminalsida är den gröna linjen, eftersom vinklarna ritas moturs. Den böjda gröna linjen visar den givna vinkeln.
även innan du har ritat vinkeln, skulle jag ha vetat att vinkeln är i den första kvadranten eftersom 30° är mellan 0 ° och 90°. Referensvinkeln, som visas av den krökta lila linjen, är densamma som den givna vinkeln.,
vinkeln 150 ° är uppenbarligen inte densamma som vinkeln 30° ;den är större och dess terminalsida ligger i den andra kvadranten (eftersom 150° är mellan 90° och 180°). Den terminalsidan är dock endast 30° från den negativa X-axeln, som du kan se av den lila linjen i ritningen:
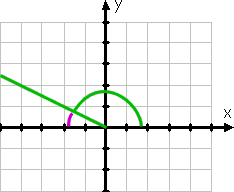
eftersom terminalsidan av 150° bara är trettio grader från (negativ) X-axeln (är trettio grader mindre än 180°, vilket är den negativa x-axeln), är referensvinkeln (igen visad av den krökta lila linjen) 30°.,
fortsätter moturs, vi kan Diagram 210°. Denna vinkel terminal sida, eftersom 210° är mellan 180 ° och 270°, är i den tredje kvadranten, och denna sida är närmast den negativa X-axeln. Eftersom 210 är trettio mer än 180, är denna vinkels terminalsida 30° förbi (det vill säga under) den negativa x-axeln.
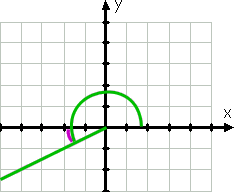
därför är referensvinkeln igen 30°.
Jag slår vad om att du kan gissa vad som skulle vara referensvinkeln för 330°., Eftersom 330 är trettio mindre än 360, och sedan 360 ° = 0°, är vinkeln 330° trettio grader under (det vill säga kort) den positiva x-axeln i fjärde kvadranten. Så dess referensvinkel är 30°.
Affiliate
Affiliate

Lägg märke till hur denna senaste beräkning gjordes. Jag hade ingen graf. Jag gjorde just aritmetiken i mitt huvud. Du bör rita grafer så länge du behöver hjälp, men var inte rädd för att börja förlita dig på aritmetiken., När du får kläm på detta, det är verkligen ganska enkelt.
Obs! eftersom referensvinkeln alltid mäter (positivt) avståndet från X-axeln kan den också ses som den första kvadrantens ekvivalenta vinkel. Med andra ord, för vart och ett av exemplen ovan, om min lärobok definierade ”referensvinkel” som ”den första kvadrantens vinkel med samma avstånd från X-axeln”, skulle den lila ”referensvinkeln” -linjen (den krökta lila linjen plus en terminalsida) ha ritats i den första kvadranten.
hur som helst kommer värdet för referensvinkeln alltid att vara detsamma., Men om du är skyldig att rita en bild som visar referensvinkeln, se till att du ritar den på den plats som anses vara ”korrekt” för din klass.
-
hitta referensvinkeln för 1500°.
jag tar min kalkylator och gör divisionen med 360° för ”once around”:
1500 trip 360 = 4.16666…
så det finns fyra cykler, plus lite. Hur mycket är bara de fyra cyklerna?
4 × 360 = 1440
det betyder att den vänstra delen (0.16666… ovan) representerar ytterligare sextio grader., Detta är mindre än nittio grader, så vinkelns terminalsida är till höger om den positiva y-axeln. Då är referensvinkeln i den första kvadranten och är lika med:
60°
innehållet fortsätter under
-
hitta den första kvadrantens referensvinkel för 954° och rita båda vinklarna på samma axelsystem.
Jag börjar med att minska denna vinkel. Hur många cykler passar inom denna vinkel?
954, 360 = 2,65
två cykler passar in i vinkeln., Hur mycket av vinkelns mått tar dessa två cykler upp?
360 × 2 = 720
hur mycket är kvar?
954 – 720 = 234
den negativa X-axeln är 180° och den negativa y-axeln är 270°. Denna vinkel är mellan dessa värden, så det är i tredje kvadranten, och kommer att vara närmast den negativa x-axeln.
hur nära? Det kommer att vara avståndet mellan terminalsidan av den reducerade vinkeln och den negativa X-axeln:
234 – 180 = 54
då är referensvinkeln:
54°
…,och ritningen är:
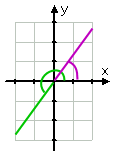
Affiliate
Lägg märke till hur jag ritade den reducerade vinkeln (som den ursprungliga vinkeln, mindre två cykler) i grönt, och sedan ritade jag den första kvadrantens referensvinkel i lila. När du gör ritningar som innehåller två (eller flera) distinkta bitar av information, kan det vara bra att ha färgpennor till hands. Ja, jag använde färgpennor på college.
-
hitta referensvinkeln för radianer.,
annons
okej, det här är i radianer. Så jag måste tänka på 0 radianer och 2π radianer för den positiva x-axeln och π radianer för den negativa x-axeln.
vinkeln de har gett mig är
radianer. Att göra divisionen för att konvertera fraktionerad form till decimalform (och ignorera π för tillfället) får jag:
16 trip 5 = 3.2
med andra ord är
radianer lika med 3.2 π radianer. En cykel är 2π radianer, så det här är lite mer än hälften-igen så mycket som en cykel., Med andra ord går denna vinkel lite förbi den negativa X-axeln:
3.2 π-2π = 1.2 π
men hur långt är terminalsidan från den negativa x-axeln?
Jag kan räkna ut detta genom att subtrahera vinkelmätningen av den negativa X-axeln från min reducerade vinkel:
1.2 π-1π
= 0.2 π
= (1/5)π
detta ger mig avståndet mellan terminalsidan av (reducerad) vinkeln och (negativ) X-axeln i radianer. Referensvinkeln är:
-
hitta referensvinkeln för radianer.,
eftersom
är mindre än 2 men mer än , då är denna vinkel i fjärde kvadranten mellan radianer och 2π radianer. Då är det närmast den positiva x-axeln. Men hur nära? Jag subtraherar för att ta reda på:
då är referensvinkeln:
oavsett om du arbetar i grader eller i radianer, så länge du vet vinkelmätningarna för x-axelns positiva och negativa delar, kan du minska vinkeln (om det behövs) och sedan göra subtraktioner för att få referensvinkeln., Om du inte är säker på ditt arbete kan du rita bilden för att vara säker. Men om du fortfarande behöver rita bilder när testet kommer upp, försök att göra lite extra övning, eftersom testet kommer att anta att du inte behöver tid att rita bilderna.
Du kan använda Mathway-widgeten nedan för att öva på att hitta medianen. Prova den angivna övningen, eller skriv in din egen övning. Klicka sedan på knappen och välj ”Hitta referensvinkeln” för att jämföra ditt svar till Mathways.,
vänligen acceptera ”inställningar” cookies för att aktivera denna widget.
(klicka på ”tryck för att visa steg” som ska tas direkt till Mathway-webbplatsen för en betald uppgradering.div>
URL:https://www.purplemath.com/modules/radians3.htm
Page 1page 2page 3
Leave a Reply