Radiani & DegreesReducing AnglesReference Unghiuri
Purplemath
În secțiunea anterioară, am găsit primul cerc unghi echivalente pentru unghi de măsuri. Un alt lucru pe care îl putem face cu măsurile de unghi, chiar și cele ale căror măsuri sunt în primul rând, este să găsim ceea ce se numește unghiul „de referință”.
unghiul de referință este unghiul pe care unghiul dat îl face cu axa X., Indiferent de locul în care se termină unghiul (adică indiferent de locația laturii terminale a unghiului), unghiul de referință măsoară cea mai apropiată distanță a acelei laturi terminale față de axa X.
conținutul continuă mai jos
MathHelp.,com

atunci Când găsirea de referință unghiuri, poate fi util să păstrați în minte că axa x pozitivă este de 0° (360° sau 0 radiani (și 2π radiani); pozitive pe axa y este de 90° sau
radiani; negativ al axei x este de 180° sau π radiani; și negative pe axa y este de 270° sau radiani.
Să începem cu un exemplu simplu., Unghiul cu măsura de 30° ar grafic astfel:
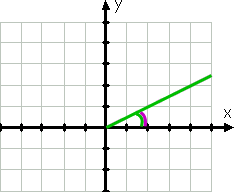
Pentru grafice, unghiul inițial este partea pozitivă a axei x; terminal parte este linia verde, pentru unghiuri sunt desenate o anti-sensul acelor de ceasornic. Linia verde curbată arată unghiul dat.chiar înainte de a desena unghiul, aș fi știut că unghiul este în primul cadran, deoarece 30° este între 0° și 90°. Unghiul de referință, indicat de linia purpurie curbată, este același cu unghiul dat.,unghiul 150°, evident, nu este același cu unghiul 30°; este mai mare, iar partea sa terminală este în al doilea cadran (deoarece 150° este între 90° și 180°). Cu toate acestea, că partea terminală este de numai 30° de la negativ al axei x, după cum puteți vedea, de violet linie în desen:
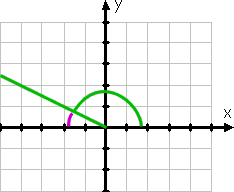
de la partea terminală a 150° este de numai treizeci de grade (negative) axa-x (curs de treizeci de grade mai puțin decât 180°, ceea ce este negativ al axei x), atunci unghiul de referință (din nou prezentate prin curbe linia mov) este de 30°.,continuând în sens invers acelor de ceasornic, putem graficul 210°. Partea terminală a acestui unghi, deoarece 210° este între 180° și 270°, se află în al treilea cadran, iar această parte este cea mai apropiată de axa x negativă. Deoarece 210 este cu treizeci mai mult decât 180, atunci partea terminală a acestui unghi este cu 30° trecut (adică sub) axa x negativă.
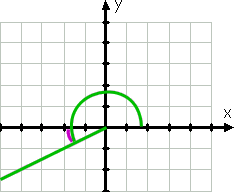
prin urmare, unghiul de referință este, din nou, 30°.pun pariu că puteți ghici care ar fi unghiul de referință pentru 330°., Deoarece 330 este treizeci mai mică decât 360 și din moment ce 360° = 0°, atunci unghiul 330° este cu treizeci de grade sub (adică scurt) axa x pozitivă, în al patrulea cadran. Deci unghiul său de referință este de 30°.
Afiliat
Afiliat

Observați cum acest ultim calcul a fost făcut. Nu am avut un grafic. Tocmai am făcut aritmetica în capul meu. Ar trebui să desenați grafice atât timp cât aveți nevoie de ajutor, dar nu vă fie frică să începeți să vă bazați pe aritmetică., Odată ce te obișnuiești cu asta, este într-adevăr destul de simplu.
notă: deoarece unghiul de referință măsoară întotdeauna distanța (pozitivă) față de axa x, acesta poate fi, de asemenea, privit ca fiind unghiul echivalent cu primul cadran. Cu alte cuvinte, pentru fiecare dintre exemplele de mai sus, dacă manualul meu a definit „unghiul de referință” ca „unghiul primului cvadrant cu aceeași distanță față de axa x”, atunci linia violet „unghiul de referință” (linia purpurie curbată, plus o latură terminală) ar fi fost trasată în primul cvadrant.
oricum, valoarea pentru unghiul de referință va fi întotdeauna aceeași., Dar dacă vi se cere să desenați o imagine care să arate unghiul de referință, asigurați-vă că o desenați în locația considerată „corectă” pentru clasa dvs.
-
găsiți unghiul de referință pentru 1500°.
voi apuca calculatorul meu și de a face Diviziunea de 360° pentru „o dată în jurul valorii de”:
1500 ÷ 360 = 4.16666…deci, există patru cicluri, plus puțin. Cât de mult este doar cele patru cicluri?
4 × 360 = 1440
asta înseamnă că porțiunea din stânga-peste (0.16666… mai sus) reprezintă încă șaizeci de grade., Aceasta este mai mică de nouăzeci de grade, astfel încât partea terminală a unghiului este la dreapta axei y pozitive. Apoi, unghiul de referință este în primul cadran și este egal cu:
60°
conținutul continuă sub
-
găsiți unghiul de referință pentru primul cadran pentru 954° și desenați ambele unghiuri pe același sistem de axe.
voi începe prin reducerea acestui unghi. Câte cicluri se încadrează în acest unghi?
954 ÷ 360 = 2,65
două cicluri se potrivesc în unghi., Cât din măsura unghiului ocupă aceste două cicluri?
360 × 2 = 720
atunci cât a mai rămas?
954 – 720 = 234
axa x negativă este de 180°, iar axa Y negativă este de 270°. Acest unghi este între aceste valori, deci este în al treilea cuadrant, și va fi cel mai apropiat de axa x negativă.
cât de aproape? Va fi distanța dintre partea terminală a unghiului redus și axa x negativă:
234 – 180 = 54
atunci unghiul de referință este:
54°
…,iar desenul este:
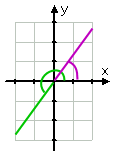
Afiliat
Observați cum am atras unghi redus (fiind unghiul original, mai puțin două cicluri) în verde, și apoi am desenat primul cadran unghiul de referință în violet. Când faceți desene care conțin două (sau mai multe) informații distincte, poate fi util să aveți creioane colorate la îndemână. Da, am folosit creioane colorate în facultate.
-
găsiți unghiul de referință pentru radiani.,
publicitate
bine, acest lucru este în radiani. Deci va trebui să mă gândesc în termeni de 0 radiani și 2π radiani pentru axa x pozitivă și π radiani pentru axa x negativă.
unghiul pe care mi l-au dat este
radiani. Fac divizia a converti fracționată formă la formă zecimală (și ignorând π pentru moment), am obține:
16 ÷ 5 = 3.2
cu alte cuvinte,
radiani este egală cu 3,2 π radiani. Un ciclu este 2π radiani, deci acesta este un pic mai mult de jumătate-din nou la fel de mult ca un ciclu., Cu alte cuvinte, acest unghi trece puțin peste axa x negativă:
3.2 π-2π = 1.2 π
dar cât de departe este partea terminală de axa x negativă?
nu pot da seama de scăderea măsura unghiul negativ al axei x din unghi redus:
1.2 π – 1π
= 0.2 π
= (1/5)π
Acest lucru îmi dă distanța între partea terminală a (redus) unghiul și (negativ) axa x în radiani. Unghiul de referință este:
-
găsiți unghiul de referință pentru radiani.,
deoarece
este mai mică decât 2 , dar mai mult decât, atunci acest unghi este în al patrulea cadran, între radiani și 2π radiani. Atunci este cel mai aproape de axa x pozitivă. Dar cât de aproape? Eu va scădea pentru a afla:
Apoi, unghiul de referință este:
Fie că sunteți de lucru în grade sau în radiani, atâta timp cât știi unghiul măsuri pozitive și negative porțiuni de axa x, puteți reduce unghiul (dacă este necesar) și apoi faceți scaderi pentru a obține unghiul de referință., Dacă nu sunteți sigur de munca dvs., puteți desena imaginea pentru a fi sigur. Dar dacă încă mai aveți nevoie să desenați imagini atunci când testul se apropie, încercați să faceți o practică suplimentară, deoarece testul va presupune că nu aveți nevoie de timp pentru a desena imaginile.puteți utiliza widget-ul Mathway de mai jos pentru a practica găsirea mediana. Încercați exercițiul introdus sau tastați propriul exercițiu. Apoi faceți clic pe buton și selectați „găsiți unghiul de referință” pentru a compara răspunsul dvs. cu cel al lui Mathway.,
vă Rog să acceptați „preferences” cookie-uri pentru a permite acest widget.
(Faceți clic pe „Apăsați pentru a vizualiza pașii” pentru a fi luate direct la site-ul Mathway pentru un upgrade plătit.mai multe detalii puteti citi aici:
Leave a Reply