
Sir Isaac Newton (1643-1727)
Na atmosfera inebriante do Século 17, na Inglaterra, com a expansão do império Britânico em pleno andamento, grand old universidades como Oxford e Cambridge foram a produção de muitos grandes cientistas e matemáticos. Mas o maior de todos era, sem dúvida, Sir Isaac Newton.,Newton é considerado por muitos como um dos homens mais influentes da história humana. Sua publicação de 1687, “Philosophiae Naturalis Principia Mathematica “(geralmente chamada simplesmente de” Principia”), é considerada como um dos livros mais influentes da história da ciência, e dominou a visão científica do universo físico pelos próximos três séculos.,embora em grande parte sinônimo na mente do público em geral hoje com a gravidade e a história da macieira, Newton permanece um gigante na mente dos matemáticos em toda parte (em um par com os grandes de todos os tempos, como Arquimedes e Gauss), e ele influenciou grandemente o caminho subsequente do desenvolvimento matemático.ao longo de dois anos milagrosos, durante o tempo da grande praga de 1665-6, o jovem Newton desenvolveu uma nova teoria da luz, descobriu e quantificou a gravitação, e foi pioneiro numa nova abordagem revolucionária à matemática: o cálculo infinitesimal., Sua teoria do cálculo construído em trabalhos anteriores por seus colegas Ingleses John Wallis e Isaac Barrow, bem como no trabalho de tal Continental matemáticos como René Descartes, Pierre de Fermat, Bonaventura Cavalieri, Johann van Waveren Hudde e Gilles Personne de Roberval. Ao contrário da geometria estática dos gregos, o cálculo permitiu que matemáticos e engenheiros fizessem sentido do movimento e da mudança dinâmica no mundo em mudança ao nosso redor, tais como as órbitas dos planetas, o movimento dos Fluidos, etc.,
A Inclinação Média da Curva
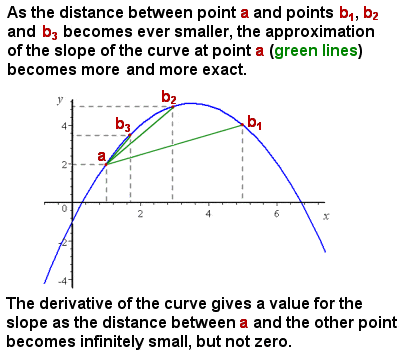
a Diferenciação (derivativos) aproxima-se a inclinação de uma curva como o intervalo tende a zero
O problema inicial Newton estava enfrentando era a de que, embora fosse fácil o suficiente para representar e calcular a média de inclinação de uma curva (por exemplo, o aumento da velocidade de um objeto em um tempo de distância do gráfico), a inclinação de uma curva foi variam constantemente, e não havia nenhum método para dar a exata inclinação em qualquer ponto específico na curva, i.é., efetivamente a inclinação de uma linha tangente à curva nesse ponto.
intuitivamente, a inclinação em um determinado ponto pode ser aproximada tomando a inclinação média (“ascensão sobre execução”) de segmentos cada vez menores da curva. À medida que o segmento da curva a ser considerado se aproxima de zero EM TAMANHO (Isto é, uma alteração infinitesimal em x), o cálculo da inclinação aproxima-se cada vez mais perto da inclinação exata em um ponto (Ver imagem à direita).,
sem entrar em detalhes complicados demais, Newton(e seu contemporâneo Gottfried Leibniz independentemente) calculou uma função derivada f ‘(x) que dá a inclinação em qualquer ponto de uma função f (x). Este processo de calcular a inclinação ou a derivada de uma curva ou função é chamado de cálculo diferencial ou diferenciação (ou, em Newton terminologia, o “método das fluxões” – ele chamou a taxa instantânea de variação em um determinado ponto em uma curva o “fluxion”, e a mudança de valores de x e de y o “fluents”)., Por exemplo, a derivada de uma linha reta do tipo f(x) = 4x é apenas 4; a derivada de uma função ao quadrado f(x) = x2 é 2x; a derivada da função cúbica f(x) = x3 é 3×2, etc. Generalizando, a derivada de qualquer função de potência f ( x) = xr é rxr-1. Outras funções derivadas podem ser indicadas, de acordo com certas regras, para funções exponenciais e logarítmicas, funções trigonométricas tais como sin(x), cos(x), etc, de modo que uma função derivada pode ser indicada para qualquer curva sem descontinuidades., Por exemplo, a derivada da curva f(x) = x4 – 5×3 + sin(x2) seria f ‘(x) = 4×3 – 15×2 + 2xcos(x2).
Tendo estabelecido a derivada da função para uma determinada curva, é fácil para cálculo de inclinação em qualquer ponto específico em que a curva, apenas inserindo um valor para x. No caso de um tempo de distância do gráfico, por exemplo, a inclinação representa a velocidade do objeto em um ponto específico.,
Método de Fluents
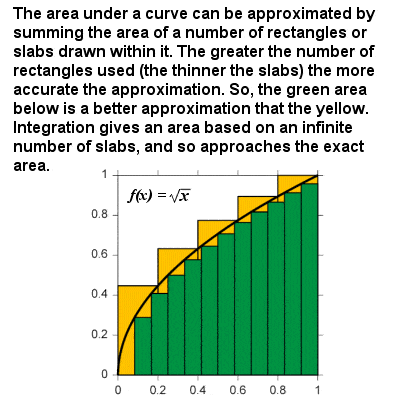
Integração aproxima-se a área sob uma curva como o tamanho das amostras tende a zero
O “oposto” de diferenciação é a integração ou cálculo integral (ou, em Newton terminologia, o “método de fluents”), e, juntos, a diferenciação e a integração são os dois principais operações de cálculo., O Teorema Fundamental de Newton do cálculo afirma que a diferenciação e integração São operações inversas, de modo que, se uma função é integrada primeiro e depois diferenciada (ou vice-versa), a função original é recuperada.
A integral de uma curva pode ser considerada como a fórmula para calcular a área delimitada pela curva e o eixo x entre dois limites definidos. Por exemplo, em um gráfico de Velocidade em relação ao tempo, a área “sob a curva” representaria a distância percorrida., Essencialmente, a integração baseia-se num procedimento limitativo que se aproxima da área de uma região curvilínea, dividindo-a em placas verticais ou colunas infinitesimalmente finas. Da mesma forma como para a diferenciação, integrante de uma função podem ser expressos em termos gerais: a integral de qualquer poder f(x) = xr xr+1⁄r+1, e existem outras integral de funções exponencial e logarítmica, funções, funções trigonométricas, etc., de modo que a área sob qualquer curva contínua pode ser obtida entre dois limites.,Newton optou por não publicar sua matemática revolucionária imediatamente, preocupado em ser ridicularizado por suas ideias não convencionais, e contentava-se com a circulação de seus pensamentos entre amigos. Afinal de contas, ele tinha muitos outros interesses, como filosofia, alquimia e seu trabalho na Casa da moeda real. No entanto, em 1684, o alemão Leibniz publicou sua própria versão independente da teoria, enquanto Newton não publicou nada sobre o assunto até 1693., Embora a Royal Society, após a devida deliberação, deu crédito para a primeira descoberta de Newton (e de crédito para a primeira publicação de Leibniz), algo de um escândalo surgiu quando foi tornado público que a Royal Society de posterior acusação de plágio contra Leibniz, na verdade, foi criado por nenhum outro senão o próprio Newton, causando um constante controvérsia que marcaram a carreira dos homens.,
Generalizada do Teorema Binomial
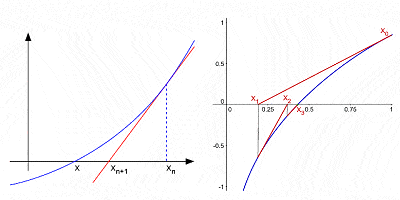
de Newton Método para aproximar as raízes de uma curva por sucessivas interacções depois de uma estimativa inicial
Apesar de ser de longe o seu melhor conhecido contribuição para a matemática, o cálculo não foi Newton apenas a contribuição.,raic expansão dos poderes de um binômio (uma expressão algébrica com dois termos, tais como, a2 – b2); ele fez grandes contribuições para a teoria das diferenças finitas (expressões matemáticas e da forma f(x + b) – f(x + a)); ele foi um dos primeiros a usar expoentes fracionários e coordenar a geometria para derivar soluções para Diophantine equações (equações algébricas com inteiro só de variáveis); ele desenvolveu o chamado “método do Newton” para encontrar sucessivamente melhores aproximações para os zeros ou raízes de uma função; ele foi o primeiro a usar o poder infinito da série com toda a confiança; etc.,em 1687, Newton publicou seu “Principia” ou “os Princípios Matemáticos da filosofia Natural”, geralmente reconhecido como o maior livro científico já escrito. Nele, ele apresentou suas teorias de movimento, gravidade e mecânica, explicou as órbitas excêntricas dos cometas, as marés e suas variações, a precessão do eixo da terra e o movimento da lua.,
mais Tarde na vida, ele escreveu uma série de folhetos religiosos lidar com a interpretação literal da Bíblia, dedicou uma grande quantidade de tempo para a alquimia, atuou como Membro do Parlamento por alguns anos, e se tornou, talvez, o mais conhecido Mestre da casa da moeda Real em 1699, uma posição que manteve até sua morte em 1727. Em 1703, foi nomeado Presidente da Royal Society e, em 1705, tornou-se o primeiro cientista a ser nomeado cavaleiro. Envenenamento por mercúrio de suas atividades alquímicas talvez tenha explicado a excentricidade de Newton No final da vida, e possivelmente também sua eventual morte.,
| << Back to Pascal | Forward to Leibniz >> |
Leave a Reply