
Statystyki są układem testów statystycznych, które analitycy wykorzystują do wnioskowania na podstawie podanych danych. Testy te pozwalają nam podejmować decyzje na podstawie obserwowanego wzorca z danych. Istnieje szeroki zakres testów statystycznych. Wybór testu statystycznego do wykorzystania zależy od struktury danych, rozkładu danych i typu zmiennej.,Istnieje wiele różnych rodzajów testów w statystykach, takich jak t-test, Z-test, chi-kwadrat test, test anova, test dwumianowy, jedna próbka mediana test itp.
wybór testu statystycznego-
testy parametryczne są używane, jeśli dane są rozkładane normalnie .Parametryczny test statystyczny sprawia, że założenie o parametrach populacji i rozkładów, że dane pochodzą z. Te typy testów obejmują testy t,testy z i testy anova, które zakładają, że dane pochodzą z rozkładu normalnego.,
Z-test – a z-test jest testem statystycznym używanym do określenia, czy dwa środki populacji różnią się, gdy wariancje są znane i wielkość próby jest duża. W badaniu z porównuje się średnią z populacji.Stosowane parametry to średnia populacji i odchylenie standardowe populacji. Z-test jest używany do potwierdzenia hipotezy, że pobrana próbka należy do tej samej populacji.,
Ho: Średnia próbki jest taka sama jak średnia populacji (hipoteza zerowa)
Ha: Średnia próbki nie jest taka sama jak średnia populacji (hipoteza Alternatywna)
z = (X — μ) / (σ / √n),
gdzie , x=średnia próbki, u=średnia populacji, σ / √n = odchylenie standardowe populacji.
Jeśli wartość z jest mniejsza niż wartość krytyczna zaakceptować hipotezę zerową inaczej odrzucić hipotezę zerową.
t-test-W teście t porównuje się średnią z dwóch podanych próbek. Badanie t stosuje się, gdy parametry populacji (średnie i odchylenie standardowe) nie są znane.,
sparowane T-Test-testy na różnicę między dwiema zmiennymi z tej samej populacji(wynik testu przed i po). Na przykład-w wyniku realizacji programu szkoleniowego stażysty przed i po zakończeniu programu.
niezależny T-test-niezależny t-test, który jest również nazywany dwoma próbkami t-test lub t-Test studenta, jest testem statystycznym, który określa, czy istnieje statystycznie istotna różnica między środkami w dwóch niepowiązanych grupach.Na przykład-porównanie chłopców i dziewcząt w populacji.,
jedna próbka t-test – średnia z jednej grupy jest porównywana z daną średnią. Na przykład-aby sprawdzić wzrost i spadek sprzedaży, jeśli podana jest średnia sprzedaż.
t = (x1 — x2) / (σ / √N1 + σ/√n2),
gdzie x1 i x2 są średnie odpowiednio dla próbki 1 i próbki 2.
Test ANOVA-Analiza wariancji (ANOVA) jest techniką statystyczną, która służy do sprawdzenia, czy środki dwóch lub więcej grup są znacznie różni się od siebie. ANOVA sprawdza wpływ jednego lub więcej czynników, porównując środki różnych próbek., Jeśli użyjemy testu t zamiast testu ANOVA, nie będzie on wiarygodny, ponieważ liczba próbek jest większa niż dwie i spowoduje to błąd w wyniku.
hipoteza badana w ANOVA to
Ho: wszystkie pary próbek są takie same, tzn., wszystkie środki próbki są równe
Ha: co najmniej jedna para próbek różni się znacząco
W teście anova obliczamy wartość F i porównujemy ją z wartością krytyczną
F= ((SSE1 — SSE2)/m)/ SSE2/n-k, gdzie
SSE = suma resztkowa kwadratów
M = liczba ograniczeń
k = liczba zmiennych niezależnych
statystyka nieparametryczna test – testy nieparametryczne są używane, gdy dane nie są rozkładane normalnie. Testy nieparametryczne obejmują test chi-kwadrat.
Test Chi-kwadrat (χ2 test) – test chi-kwadrat służy do porównania dwóch zmiennych kategorycznych., Obliczenie wartości statystycznej Chi-kwadrat i porównanie jej z wartością krytyczną z rozkładu Chi-kwadrat pozwala ocenić, czy obserwowana częstotliwość znacznie różni się od oczekiwanej częstotliwości.
hipoteza badana dla kwadratu chi jest-
Ho: zmienna x i zmienna y są niezależne
Ha: zmienna x i zmienna y nie są niezależne.,
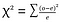
where o=observed , e=expected.
Leave a Reply