
statistieken zijn de opstelling van statistische tests die analisten gebruiken om conclusies te trekken uit de gegeven gegevens. Deze tests stellen ons in staat om beslissingen te nemen op basis van waargenomen patronen uit gegevens. Er is een breed scala aan statistische tests. De keuze van welke statistische test te gebruiken is afhankelijk van de structuur van de gegevens, de verdeling van de gegevens, en variabele type.,Er zijn vele verschillende soorten tests in statistieken zoals t-test, z-test, chi-kwadraattest, anova-test, binomiale test, één steekproef mediaan test enz.
een statistische test kiezen –
parametrische tests worden gebruikt als de gegevens normaal worden verspreid .Een parametrische statistische test maakt een aanname over de populatie parameters en de distributies waar de gegevens vandaan kwamen. Deze soorten tests omvatten t-tests, z-tests en anova-tests, waarbij wordt aangenomen dat de gegevens afkomstig zijn van normale distributie.,
Z-test – een z-test is een statistische test die wordt gebruikt om te bepalen of twee populatiegemiddelden verschillen wanneer de varianties bekend zijn en de steekproefgrootte groot is. In de z-test wordt het gemiddelde van de populatie vergeleken.De gebruikte parameters zijn de gemiddelde populatie en de standaardafwijking van de populatie. Z-test wordt gebruikt om een hypothese te valideren dat de getrokken steekproef tot dezelfde populatie behoort.,
Ho: het steekproefgemiddelde is hetzelfde als het populatiegemiddelde(nulhypothese)
Ha: het steekproefgemiddelde is niet hetzelfde als het populatiegemiddelde (alternatieve hypothese)
z = (X — μ) / (σ / √n),
waarbij , x=steekproefgemiddelde, u=populatiegemiddelde, σ / √n = standaarddeviatie van de populatie.
als de z-waarde kleiner is dan de kritische waarde accepteer nulhypothese anders weiger nulhypothese.
T-test – in t-test wordt het gemiddelde van de twee gegeven monsters vergeleken. Een t-test wordt gebruikt wanneer de populatieparameters (gemiddelde en standaardafwijking) niet bekend zijn.,
gepaarde T-Test-Tests voor het verschil tussen twee variabelen van dezelfde populatie( pre – en posttestscore). Bijvoorbeeld – in een trainingsprogramma performance score van de stagiair voor en na voltooiing van het programma.
onafhankelijke T-test-de onafhankelijke t-test die ook wel de twee steekproef t-test of student t-test wordt genoemd, is een statistische test die bepaalt of er een statistisch significant verschil is tussen de gemiddelden in twee niet-gerelateerde groepen.Bijvoorbeeld-het vergelijken van jongens en meisjes in een populatie.,
één monster t-test-Het gemiddelde van een enkele groep wordt vergeleken met een bepaald gemiddelde. Bijvoorbeeld-om de stijging en daling van de verkoop te controleren als de gemiddelde verkoop wordt gegeven.
t =(x1-x2) / (σ / √n1 + σ/√n2),
waarbij x1 en x2 respectievelijk het gemiddelde van monster 1 en monster 2 zijn.
ANOVA-variantietest (ANOVA) is een statistische techniek die wordt gebruikt om te controleren of de gemiddelden van twee of meer groepen significant van elkaar verschillen. ANOVA controleert het effect van een of meer factoren door de middelen van verschillende monsters te vergelijken., Als we gebruik maken van een t-test in plaats van ANOVA test zal het niet betrouwbaar zijn als aantal monsters zijn meer dan twee en het zal fout in het resultaat geven.
de hypothese die in ANOVA wordt getest is
Ho: Alle paar monsters zijn hetzelfde, d.w.z., alle steekproefgemiddelden zijn gelijke
Ha: Ten minste een paar van de monsters is significant verschillend
In de anova-test we berekenen F-waarde en het vergelijken met de kritische waarde
F= ((SSE1 — SSE2)/m)/ SSE2/n-k, waar
ZW = residuele som van kwadraten
m = aantal beperkingen
k = aantal onafhankelijke variabelen
Niet-parametrische statistische testen – Niet-parametrische tests worden gebruikt wanneer de gegevens niet normaal verdeeld. Niet-parametrische tests omvatten chi-kwadraattest.
Chi-kwadraattest (χ2-test)-chi-kwadraattest wordt gebruikt om twee categorische variabelen te vergelijken., Het berekenen van de chi-kwadraat statistische waarde en het vergelijken van deze met een kritische waarde van de Chi-kwadraatverdeling maakt het mogelijk om te beoordelen of de waargenomen frequentie significant verschilt van de verwachte frequentie.
de hypothese die wordt getest voor het chi-kwadraat is-
Ho: variabele x en variabele y zijn onafhankelijk
Ha: variabele x en variabele y zijn niet onafhankelijk.,
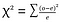
where o=observed , e=expected.
Leave a Reply