radialen & DegreesReducing Anglesreferentiehoeken
Purplemath
In de vorige sectie, vonden we de eerste-cirkel hoek equivalenten voor bepaalde hoek maatregelen. Een ander ding dat we kunnen doen met hoekmetingen, zelfs die waarvan de maatregelen in de eerste doorstart zijn, is het vinden van wat de “referentie” hoek wordt genoemd.
de referentiehoek is de hoek die de gegeven hoek maakt met de x-as., Ongeacht waar de hoek eindigt (dat wil zeggen, ongeacht de locatie van de eindzijde van de hoek), meet de referentiehoek de dichtstbijzijnde afstand van die eindzijde tot de x-as.
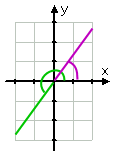
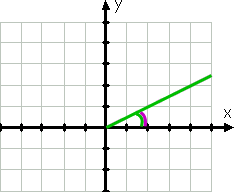
laten we beginnen met een eenvoudig voorbeeld., De hoek met maat 30° zou als volgt kunnen worden weergegeven:
Voor grafieken is de beginzijde van de hoek de positieve x-as; de eindzijde is de groene lijn, omdat hoeken tegen de klok in worden getekend. De gebogen groene lijn toont de gegeven hoek.
zelfs voordat ik de hoek had getekend, had ik geweten dat de hoek in het eerste kwadrant ligt omdat 30° tussen 0° en 90°ligt. De referentiehoek, weergegeven door de gebogen paarse lijn, is dezelfde als de gegeven hoek.,
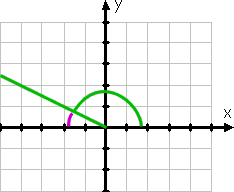
de hoek 150° is natuurlijk niet hetzelfde als de hoek 30°; Het is groter en de eindzijde bevindt zich in het tweede kwadrant (omdat 150° tussen 90° en 180°ligt). Echter, die terminal zijde is slechts 30° van de negatieve x-as, zoals je kunt zien aan de paarse lijn in de tekening:
aangezien de terminal zijde van de 150° is slechts dertig graden van de (negatieve) x-as (zijnde dertig graden minder dan 180°, dat is de negatieve X-as), dan is de referentie hoek (opnieuw weergegeven door de gebogen paarse lijn) 30°.,
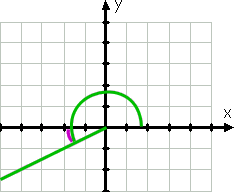
Doorgaan rond tegen de klok in, kunnen we grafiek 210°. De eindzijde van deze hoek, omdat 210° tussen 180° en 270° ligt, bevindt zich in het derde kwadrant, en deze kant ligt het dichtst bij de negatieve x-as. Omdat 210 dertig meer is dan 180, dan is de eindzijde van deze hoek 30° voorbij (dat wil zeggen, onder) de negatieve x-as.
daarom is de referentiehoek wederom 30°.
Ik wed dat je kunt raden wat de referentiehoek voor 330°zou zijn., Omdat 330 dertig minder is dan 360, en omdat 360° = 0°, dan is de hoek 330° dertig graden onder (dat wil zeggen, kort van) de positieve x-as, in het vierde kwadrant. Dus de referentiehoek is 30°.
Affiliate
Affiliate
merk op hoe deze laatste berekening werd uitgevoerd. Ik had geen grafiek. Ik heb net het rekenwerk in mijn hoofd gedaan. Je moet grafieken tekenen voor zo lang als je de hulp nodig hebt, maar wees niet bang om te vertrouwen op de rekenkunde., Als je dit eenmaal onder de knie hebt, is het heel eenvoudig.
Opmerking: Omdat de referentiehoek altijd de (positieve) afstand van de x-as meet, kan deze ook worden gezien als de eerste kwadrant-equivalente hoek. Met andere woorden, voor elk van de bovenstaande voorbeelden, als mijn leerboek “referentiehoek” definieerde als “de eerste kwadranthoek met dezelfde afstand van de x-as”, dan zou de paarse “referentiehoek” lijn (de gebogen paarse lijn, plus een eindzijde) in het eerste kwadrant zijn getekend.
hoe dan ook, de waarde voor de referentiehoek zal altijd hetzelfde zijn., Maar als je verplicht bent om een afbeelding te tekenen die de referentiehoek laat zien, zorg er dan voor dat je deze tekent op de locatie die als “correct” wordt beschouwd voor je klas.
-
Zoek de referentiehoek voor 1500°.
Ik pak mijn calculator en doe de deling door 360° voor “eenmaal rond”:
dus er zijn vier cycli, plus een beetje. Hoeveel is alleen de vier cycli?
dat betekent dat het overgebleven gedeelte (de 0,16666… boven) vertegenwoordigt nog eens zestig graden., Dit is kleiner dan negentig graden, dus de eindzijde van de hoek is rechts van de positieve y-as. Dan is de referentiehoek in het eerste kwadrant en is gelijk aan:
inhoud gaat verder onder
-
Zoek de referentiehoek van de eerste kwadrant voor 954°en teken beide hoeken op hetzelfde assysteem.
Ik begin met het verkleinen van deze hoek. Hoeveel cycli passen binnen deze hoek?
twee cycli passen binnen de hoek., Hoeveel van de maat van de hoek nemen die twee cycli in beslag?
hoeveel blijft er dan over?
de negatieve x-as is 180° en de negatieve y-as is 270°. Deze hoek is tussen deze waarden, dus het is in het derde kwadrant, en zal het dichtst bij de negatieve x-as.
hoe dichtbij? Het zal de afstand zijn tussen de eindzijde van de gereduceerde hoek en de negatieve x-as:
dan is de referentiehoek:
…,en de tekening is:
Affiliate
merk op hoe ik de gereduceerde hoek tekende (zijnde de oorspronkelijke hoek, min twee cycli) in groen, en dan tekende ik de eerste kwadrant referentiehoek in paars. Wanneer u tekeningen maakt die twee (of meer) afzonderlijke stukjes informatie bevatten, kan het nuttig zijn om kleurpotloden bij de hand te hebben. Ja, ik gebruikte kleurpotloden op de universiteit.
-
Zoek de referentiehoek voor radialen.,
OK, dit is in radialen. Dus ik moet denken in termen van 0 radialen en 2π radialen voor de positieve x-as, en π radialen voor de negatieve x-as.
de hoek die ze me hebben gegeven is
radialen. Door de deling te doen om de fractionele vorm om te zetten in decimale vorm (en de π Voor het moment te negeren), krijg ik:
met andere woorden,
radialen is gelijk aan 3.2 π radialen. Een cyclus is 2π radialen, dus dit is een beetje meer dan de helft-opnieuw zo veel als één cyclus., Met andere woorden, deze hoek gaat een beetje voorbij de negatieve x-as:
maar hoe ver is de eindzijde van de negatieve x-as?
Ik kan dit berekenen door de hoekmaat van de negatieve x-as af te trekken vanuit mijn gereduceerde hoek:
Dit geeft me de afstand tussen de eindzijde van de (gereduceerde) hoek en de (negatieve) x-as in radialen. De referentiehoek is:
radialen
-
Zoek de referentiehoek voor radialen.,
aangezien
kleiner is dan 2 maar meer dan , dan is deze hoek in het vierde kwadrant, tussen radialen en 2π radialen. Dan is het het dichtst bij de positieve x-as. Maar hoe dichtbij? Ik trek af om erachter te komen:
dan is de referentiehoek:
radialen
of u nu in graden of in radialen werkt, zolang u weet dat de hoek meet voor de positieve en negatieve delen van de x-as, kunt u de hoek (indien nodig) verkleinen en vervolgens aftrekken om de referentiehoek te krijgen., Als u niet zeker bent van uw werk, kunt u de tekening om zeker te zijn. Maar als je nog steeds foto ’s moet tekenen als de test eraan komt, probeer dan wat extra oefening te doen, want de test gaat ervan uit dat je geen tijd nodig hebt om de foto’ s te tekenen.
u kunt de Mathway widget hieronder gebruiken om te oefenen met het vinden van de mediaan. Probeer de ingevoerde oefening, of typ in uw eigen oefening. Klik vervolgens op de knop en selecteer “Find the Reference Angle” om je antwoord te vergelijken met dat van Mathway.,
accepteer” preferences ” cookies om deze widget in te schakelen.
(klik op “Tap to view steps” om direct naar de Mathway site te gaan voor een betaalde upgrade.)
URL: https://www.purplemath.com/modules/radians3.htm



Leave a Reply