
Sir Isaac Newton(1643-1727)
에서 앞뒤를 헤아 리지 않는 분위기의 17 세기 영국의 확장으로 대영 제국에 한창이고,그랜드 올드 옥스포드 대학과 케임브리지 생산되는 많은 훌륭한 과학자들과 수학자. 그러나 그들 중 가장 위대한 사람은 의심 할 여지없이 아이작 뉴턴 경이었습니다.,
물리학자,수학자,천문학자,자연의 철학자,연금술사와 신학자 뉴턴은 많은 것으로 간주됩 하나의 가장 영향력 있는 남자에서 인간의 역사입니다. 그 1687 게시”Philosophiae 수학적 원리 원리”(일반적으로 불리는 단순히”원리”),고려할 중 가장 영향력 있는 책에서 과학의 역사,그리고 지배하는 과학적 관점의 물리적 우주에 대해 다음 세 가지다.,
지만 주로 동의어 마음에서 일반 대중의 오늘을 가진 중력의 이야기와 사과 나무,뉴턴은 마음에서의 수학자들은 어디에나(와 동등하게 모든 시간은 같은 유명한 선수는 아르키메데스와 가우스),그리고 그는 크게 영향을 받은 후의 경로는 수학적 개발.
두 가지 이상의 기적 년이 시간 동안,위대한 전염병의 1665-6,젊은 뉴턴의 새로운 이론,빛을 발견하고 정량화하는 인력,그리고 개척했는 혁신적인 새로운 접근 방법의 수학:무한 미적분., 그의 이론을 수학 내에서 이전 작업에 의해 그의 동료 영국인 죤 월리스와 이삭의 배로,뿐 아니라 작업의 이러한 수학자들은 유럽대륙으로 René Descartes,피에르 드 Fermat,Bonaventura 카발리에리,요한 반 Waveren Hudde 및 질 Personne 드 로베르발. 달리 정적 형상의 그리스,미적분학을 허용되는 수학자 및 엔지니어들이 감각을 만들의 움직임과 역동적인 변화에서 변화하는 세계를 우리 주변과 같은 행성의 궤도,운동,유체의 등입니다.,
평균 경사면의 곡선
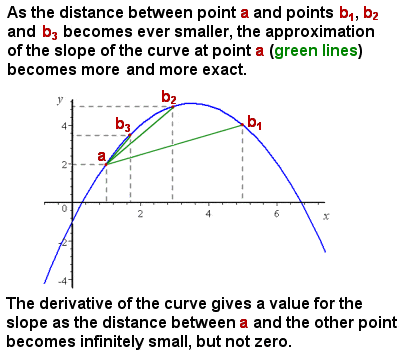
차별화(유도체)에 근접의 경사면에 곡선을 간격으로 접근 제
초기 문제 뉴턴이 직면하고 있었지만,그것은 쉬운을 표현하기에 충분하고 평균을 계산 경사면의 곡선(예를 들어, 증가하는 속도로에 물체의 시간 거리 그래프),사면의 곡선은 끊임없이 변화가 없었음이 방법을 제공한 정확한 경사면에는 어떤 하나의 개별 점 곡선에서 즉, 효과적으로 해당 지점에서 곡선에 대한 접선 선의 기울기입니다.
직관적으로,특정 지점에서의 기울기는 곡선의 더 작은 세그먼트의 평균 기울기(“rise over run”)를 취하여 근사 할 수 있습니다. 으로 세그먼트의 곡선 고려되는 접근 방식에서 제로 크기(즉,무한 변 x),다음의 계산 경사에 가까이 접근과 더 가까이 정확한 슬로프에서 포인트(이미지를 참조하십시오에서 오른쪽).,
으로 가지 않고 너무 복잡한 세부사항,뉴턴(과 그 현대적인리프트 라이프는 독립적으로)계산 유도체 기능을 f(x)을 제공하는 경사가 모든 지점에서의 기능을 f(x) 이 과정을 계산하는 경사 또는 파생물의 곡선 또는 함수가 호출되는 차등적분 또는 차별화(또는에,뉴톤의 용어,의 방법”fluxions”–그라는 즉각적인 변화율에서 특정 시점에서 커브는”fluxion”,그리고 변화하는 x y 값이”fluents”)., 예를 들어,f(x)=4x 유형의 직선의 파생은 단지 4 이고,제곱 함수 f(x)=x2 의 파생은 2 배이며,입방 함수 f(x)=x3 의 파생은 3×2 등입니다. 일반화하면 모든 전력 함수 f(x)=xr 의 파생물은 rxr-1 입니다. 기타 유도체 기능을 할 수 있습니다 stated,일정한 규칙에 따라,대한 기하 급수적으로 로그 함수,삼각함수와 같은 죄(x),cos(x)등도록 유도체 기능을 수 있습 명시된 어떠한 곡선 없이 불연속성., 예를 들어 곡선 f(x)=x4–5×3+sin(x2)의 파생물은 f'(x)=4x3–15×2+2xcos(x2)가됩니다.
를 설립하는 데 유도체 기능에 대한 특정한 곡선,그것은 쉬운 문제를 calcuate 사에서 특정 시점에서는 단지를 삽입하여 값 x. 의 경우에는 시간 거리를 그래프로,예를 들어,이 경사의 속도를 나타내는 객체의 특정 지점에서.,
방법 Fluents
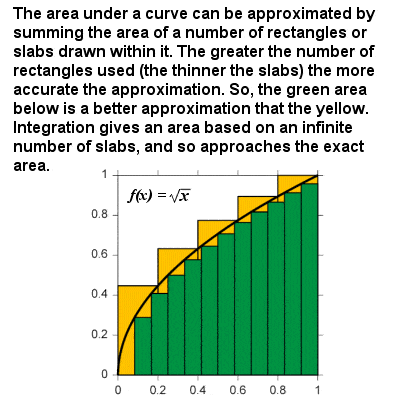
통합 근접 지역에서는 곡으로 크기의 샘플 접근 제
“반대”의 차별화가 통합 또는 필수적인 수학(또는에,뉴톤의 용어,의 방법”fluents”), 과 함께 차별화하고 통합하는 두 가지 주요 작업의 발생합니다., 뉴턴의 근본적인 정리를 수학의 상태는 차별화 및 통합은 역 작업,그래서는,함수의 경우 최초의 통합과 그의 차별화된(또는 그 반대로),원래의 함수를 검색합니다.
곡선의 적분은 두 정의 된 경계 사이의 곡선과 x 축에 의해 경계가되는 면적을 계산하는 공식으로 생각할 수 있습니다. 예를 들어,시간에 대한 속도의 그래프에서”곡선 아래”영역은 이동 한 거리를 나타냅니다., 기본적으로 통합에 기반한 절차에 근접하는 지역의 곡선은 지역을 파괴하여 그것으로 미소하게 얇은 수직판 또는 열이 있습니다. 에서와 동일한 방식으로 차별화,완전한 기능을 언급 할 수있다 일반적인 관점에서:정수의 어떤 힘 f(x)=xr 은 xr+1⁄r+1,및 다른 핵심 기능에 대한 기하 급수적으로 로그 함수,삼각함수,등록,이 지역에서 지속적인 곡선을 얻을 수 있는 사이에 어떤 제한을 두.,
뉴턴을 선택했 공개하지 않도록 자신의 획기적인 수학을 바,걱정되는 조롱에 대한 자신의 틀에 얽매이지 않는 아이디어를,그리고 만족하게 자신과 함께 순환하는 그의 생각을 합니다. 결국,그는 철학,연금술 및 로얄 민트에서의 그의 작업과 같은 다른 많은 관심사를 가지고있었습니다. 그러나 1684 년 독일 라이프니츠는 자신의 독립적 인 이론 버전을 발표 한 반면 뉴턴은 1693 년까지 주제에 대해 아무 것도 발표하지 않았다., 하지만 왕 사회,후으로 인해 심의를 준용한 첫 번째 검색하는 뉴톤(및 신용을 위한 첫 번째 간행물을 Leibniz),무언가의 사건이 일어나면 그것이 공개되었다는 왕의 사회의 이후의 비난의 표절에 대한 Leibniz 실제로 제작하여 전혀 다른 뉴턴은 자신이 원인,지속적인 논쟁는 손상의 경력을 모두 남자입니다.,
일반화 이항 정리
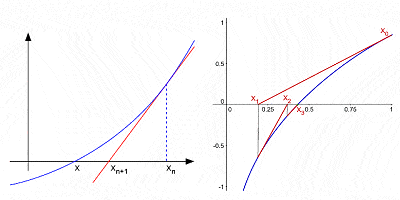
뉴턴의 방법을 뿌리에 가깝게 곡선의에 의해 연속적으로 interations 후 초기 추측
에도 불구하고 지금까지 자신의 가장 잘 알려진에 기여 수학,미적분학 의미가 없었 뉴턴의 유일한 공헌이다.,raic 의 확장의 힘을 이항(대수적 표현으로 두 가지 조건과 같은 a2–b2);그가 상당한 기여를 만들어의 이론 유한 차이(수학적 표현의 형태로 f(x+b)f(x+a));그 첫 번째 중 하나를 사용하여 소수의 지수 및 좌표 형상 파생하는 솔루션을 Diophantine 방정식(대수적 방정식과 정수 변수만); 그가 개발한 소위”뉴턴의 방법”을 찾기 위한 연속적으로 더 나은 근사하 제로 또는 뿌리의 기능이었으며,그 사용하는 첫번째 시리즈는 무한한 힘으로 어떤 신뢰;etc.,
에 1687,뉴턴이 출판되”원리”또는”수학적 원리의 자연적인 철학”,일반적으로 인정으로서 최고의 과학적인 책입니다. 에 그것은,그가 그의 이론들의 운동,중력 및 기계,설명은 괴상한 혜성의 궤도,파도 그들의 변형,운동이 지구의 축 모션습니다.,
생활에서 나중에,그가 쓴 다수의 종교적 책자를 다루는 문자와 해석,성경의 헌신적인 좋은 거래를 하는 시간의 연금술,행동으로 의회의 구성원에 대한 몇 년이 되었고 아마도 가장 잘 알려진 마스터의 왕 박하에 1699,그는 열린에서 죽음까지 1727. 1703 년에 그는 왕립 학회 회장이되었고,1705 년에 기사 작위를받은 최초의 과학자가되었습니다. 수은 중독에서의 연금술활동도 설명했 뉴턴의 편심이 나중에 생활에,그리고 아마도 그의 궁극적인 죽음입니다.,
| << Back to Pascal | Forward to Leibniz >> |
Leave a Reply