
Sir Isaac Newton (1643-1727)
Nell’inebriante atmosfera del 17 ° Secolo in Inghilterra, con l’espansione dell’impero Britannico in pieno svolgimento, il grand old università come Oxford e Cambridge sono stati la produzione di molti grandi scienziati e matematici. Ma il più grande di tutti era senza dubbio Sir Isaac Newton.,
Fisico, matematico, astronomo, filosofo naturale, alchimista e teologo, Newton è considerato da molti uno degli uomini più influenti della storia umana. La sua pubblicazione del 1687, la” Philosophiae Naturalis Principia Mathematica “(di solito chiamata semplicemente” Principia”), è considerata tra i libri più influenti nella storia della scienza, e ha dominato la visione scientifica dell’universo fisico per i successivi tre secoli.,
Anche se in gran parte sinonimo nella mente del grande pubblico di oggi con la gravità e la storia del melo, Newton rimane un gigante nella mente dei matematici di tutto il mondo (alla pari con i grandi di tutti i tempi come Archimede e Gauss), e ha notevolmente influenzato il successivo percorso di sviluppo matematico.
In due anni miracolosi, durante il periodo della Grande Peste del 1665-6, il giovane Newton sviluppò una nuova teoria della luce, scoprì e quantificò la gravitazione, e fu pioniere di un nuovo approccio rivoluzionario alla matematica: il calcolo infinitesimale., La sua teoria del calcolo si basa su precedenti lavori dei suoi colleghi inglesi John Wallis e Isaac Barrow, così come sul lavoro di matematici continentali come René Descartes, Pierre de Fermat, Bonaventura Cavalieri, Johann van Waveren Hudde e Gilles Personne de Roberval. A differenza della geometria statica dei greci, il calcolo ha permesso a matematici e ingegneri di dare un senso al movimento e al cambiamento dinamico nel mondo che cambia intorno a noi, come le orbite dei pianeti, il movimento dei fluidi, ecc.,
La Pendenza Media di una Curva
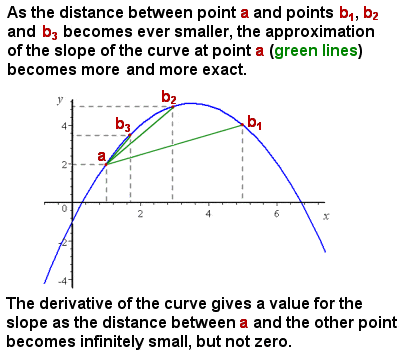
la Differenziazione (derivati) approssima la pendenza di una curva, mentre l’intervallo si avvicina a zero
Il problema iniziale Newton era affrontare è che, anche se è stato abbastanza facile per rappresentare e calcolare la pendenza media di una curva (per esempio, l’incremento della velocità di un oggetto in un tempo-distanza grafico), la pendenza di una curva è stata variano costantemente, e non c’era alcun metodo per dare l’esatta pendenza a qualsiasi individuo un punto sulla curva cioè, effettivamente la pendenza di una linea tangente alla curva in quel punto.
Intuitivamente, la pendenza in un particolare punto può essere approssimata prendendo la pendenza media (“rise over run”) di segmenti sempre più piccoli della curva. Quando il segmento della curva considerata si avvicina a zero in termini di dimensioni (cioè un cambiamento infinitesimale in x), allora il calcolo della pendenza si avvicina sempre più alla pendenza esatta in un punto (vedi immagine a destra).,
Senza entrare nei dettagli troppo complicati, Newton (e il suo contemporaneo Gottfried Leibniz indipendentemente) calcolarono una funzione derivata f ‘(x) che dà la pendenza in qualsiasi punto di una funzione f(x). Questo processo di calcolo della pendenza o derivata di una curva o di una funzione è chiamato calcolo differenziale o differenziazione (o, nella terminologia di Newton, il “metodo dei flussi” – ha chiamato la velocità istantanea di cambiamento in un particolare punto su una curva la “fluxion”, ei valori mutevoli di x e y i “fluenti”)., Ad esempio, la derivata di una linea retta del tipo f(x) = 4x è solo 4; la derivata di una funzione quadrata f(x) = x2 è 2x; la derivata della funzione cubica f(x) = x3 è 3×2, ecc. Generalizzando, la derivata di qualsiasi funzione di potenza f (x) = xr è rxr-1. Altre funzioni derivate possono essere dichiarate, secondo alcune regole, per funzioni esponenziali e logaritmiche, funzioni trigonometriche come sin(x), cos(x), ecc., in modo che una funzione derivata possa essere dichiarata per qualsiasi curva senza discontinuità., Ad esempio, la derivata della curva f(x) = x4 – 5×3 + sin(x2) sarebbe f ’(x) = 4×3 – 15×2 + 2xcos(x2).
Avendo stabilito la funzione derivata per una particolare curva, è quindi facile calcolare la pendenza in un particolare punto di quella curva, semplicemente inserendo un valore per x. Nel caso di un grafico a distanza temporale, ad esempio, questa pendenza rappresenta la velocità dell’oggetto in un particolare punto.,
il Metodo di Fluents
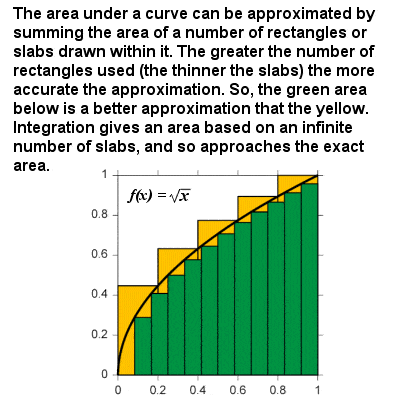
Integrazione approssima l’area sotto una curva come la dimensione dei campioni si avvicina a zero
“contrario” di differenziazione è l’integrazione o calcolo integrale (o di Newton, la terminologia, il “metodo di fluents”), e, insieme, la differenziazione e l’integrazione sono le due principali operazioni di calcolo., Il Teorema Fondamentale del Calcolo di Newton afferma che la differenziazione e l’integrazione sono operazioni inverse, in modo che, se una funzione viene prima integrata e poi differenziata (o viceversa), la funzione originale viene recuperata.
L’integrale di una curva può essere pensato come la formula per calcolare l’area delimitata dalla curva e l’asse x tra due confini definiti. Ad esempio, su un grafico di velocità contro il tempo, l’area “sotto la curva” rappresenterebbe la distanza percorsa., Essenzialmente, l’integrazione si basa su una procedura limitante che approssima l’area di una regione curvilinea suddividendola in lastre o colonne verticali infinitesimalmente sottili. Allo stesso modo, una differenziazione, una funzione integrale può essere espressa in termini generali: l’integrale di qualsiasi potenza f(x) = xr è xr+1⁄r+1, e ci sono altre funzioni esponenziali e funzioni logaritmiche, funzioni trigonometriche, ecc, in modo che l’area sotto qualsiasi curva continua che può essere ottenuta tra due limiti.,
Newton ha scelto di non pubblicare la sua matematica rivoluzionaria subito, preoccupato di essere ridicolizzato per le sue idee non convenzionali, e si accontentò di far circolare i suoi pensieri tra amici. Dopo tutto, aveva molti altri interessi come la filosofia, l’alchimia e il suo lavoro alla Zecca Reale. Tuttavia, nel 1684, il tedesco Leibniz pubblicò la sua versione indipendente della teoria, mentre Newton non pubblicò nulla sull’argomento fino al 1693., Anche se la Royal Society, dopo la dovuta deliberazione, diede credito per la prima scoperta a Newton (e credito per la prima pubblicazione a Leibniz), qualcosa di uno scandalo sorse quando fu reso pubblico che la successiva accusa della Royal Society di plagio contro Leibniz era in realtà scritta da nessun altro Newton stesso, causando una controversia continua che ha rovinato la carriera di entrambi gli uomini.,
Teorema binomiale generalizzato
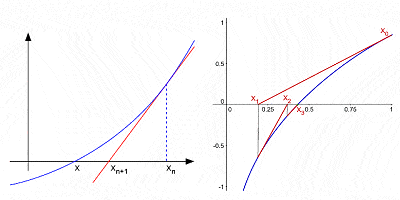
Il metodo di Newton per approssimare le radici di una curva con successive interazioni dopo un’ipotesi iniziale
Nonostante fosse di gran lunga il suo contributo più noto alla matematica, il calcolo non fu affatto l’unico contributo di Newton.,raic espansione delle potenze di un binomio (un’espressione algebrica con due termini, come a2 – b2); ha fatto importanti contributi alla teoria delle differenze finite (matematica espressioni della forma f(x + b) – f(x + a)); fu uno dei primi ad utilizzare esponenti frazionari e coordinare geometria derivare soluzioni alle equazioni Diofantee (equazioni algebriche intere variabili); ha sviluppato il cosiddetto “metodo di Newton” per la ricerca di migliori successivamente approssimazioni del zeri o radici di una funzione; egli fu il primo a utilizzare la potenza infinita serie con sicurezza; etc.,
Nel 1687, Newton pubblicò il suo “Principia” o “The Mathematical Principles of Natural Philosophy”, generalmente riconosciuto come il più grande libro scientifico mai scritto. In esso, ha presentato le sue teorie di movimento, gravità e meccanica, ha spiegato le orbite eccentriche delle comete, le maree e le loro variazioni, la precessione dell’asse terrestre e il moto della Luna.,
Più tardi, scrisse una serie di trattati religiosi riguardanti l’interpretazione letterale della Bibbia, dedicò molto tempo all’alchimia, fu membro del Parlamento per alcuni anni e divenne forse il più noto Maestro della Zecca Reale nel 1699, posizione che mantenne fino alla sua morte nel 1727. Nel 1703, fu nominato Presidente della Royal Society e, nel 1705, divenne il primo scienziato ad essere nominato cavaliere. Avvelenamento da mercurio dai suoi inseguimenti alchemici forse spiegato eccentricità di Newton in età avanzata, e forse anche la sua eventuale morte.,
| << Back to Pascal | Forward to Leibniz >> |
Leave a Reply