Radians & DegreesReducing AnglesReference szögek
Purplemath
az előző szakaszban megtaláltuk az első kör szögegyenértékeit az adott szögmérésekhez. Egy másik dolog, amit tehetünk a szögmérésekkel, még azok is, akiknek intézkedései az első körben vannak, az, hogy megtaláljuk az úgynevezett “referencia” szöget.
a referenciaszög az a szög, amelyet az adott szög az x tengelyhez ad., Függetlenül attól, hogy hol végződik a szög (azaz függetlenül a szög terminális oldalának helyétől), a referenciaszög az adott terminál oldalának az x tengelyhez legközelebbi távolságát méri.
A tartalom
MathHelp alatt folytatódik.,com

Ha a megállapítás referencia szög, ez hasznos lehet, hogy ne feledje, hogy a pozitív x tengely 0° (illetve 360° – os vagy 0 radián (pedig 2π radián); a pozitív y-tengely 90° – os, vagy
radián; a negatív x-tengely körül 180° – os, vagy π radián; a negatív y-tengely 270° – os vagy a radián.
kezdjük egy egyszerű példával., A szög intézkedés 30° volna, grafikon, mint ez:
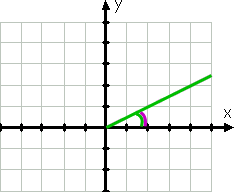
A grafikus, a szög eredeti oldalon van a pozitív x tengely; a terminál oldalán a zöld vonal, mert szögek húzott megy az óramutató járásával ellentétes irányba. Az ívelt zöld vonal mutatja az adott szöget.
még a szög rajzolása előtt is tudtam volna, hogy a szög az első kvadránsban van, mert a 30° 0° és 90°között van. A görbe lila vonal által mutatott referenciaszög ugyanaz, mint az adott szög.,
a 150° szög nyilvánvalóan nem ugyanaz, mint a 30° – os szög; nagyobb, és a terminális oldala a második kvadránsban van (mert a 150° 90° és 180°között van). Azonban, hogy a terminál oldalán csak 30° a negatív x tengely, mint ahogy láthatjuk, a lila vonal a rajzon:
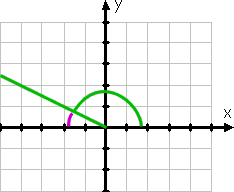
Mivel a terminál oldalán a 150° csak harminc fok a (negatív) x-tengely (mivel harminc fokkal kevesebb, mint 180° – ban, amely a negatív x tengely), akkor a referencia szög (ismét látható a görbe lila vonal) 30°.,
az óramutató járásával ellentétes irányban folytatva 210° – os grafikont tudunk ábrázolni. Ez a szög terminális oldala, mivel a 210° 180 és 270° között van, a harmadik kvadránsban van, és ez az oldal áll a legközelebb a negatív x-tengelyhez. Mivel a 210 harminczal több, mint 180, akkor ez a szög terminális oldala 30°-kal van a negatív x-tengely előtt (azaz alatt).
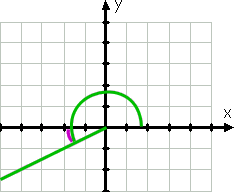
ezért a referenciaszög ismét 30°.
fogadok, hogy kitalálhatja, mi lenne a 330° – os referenciaszög., Mivel a 330 harminc kevesebb, mint 360, mivel 360° = 0°, akkor a 330° szög harminc fokkal alacsonyabb (azaz rövid) a pozitív x-tengely alatt, a negyedik kvadránsban. Tehát referenciaszöge 30°.
Affiliate
Affiliate

. Nem volt grafikonom. Csak a számtani a fejemben. Rajzoljon grafikonokat mindaddig, amíg szüksége van a segítségre, de ne féljen elkezdeni támaszkodni az aritmetikára., Egyszer kap a nyitjára, ez tényleg elég egyszerű.
Megjegyzés: Mivel a referenciaszög mindig az x tengelytől való (pozitív) távolságot méri, úgy is tekinthető, hogy az első kvadráns egyenértékű szög. Más szóval, minden a fenti példák, ha a tankönyv meghatározott “referencia szög,” mint “az első-kvadránsban szög, ugyanaz a távolság az x-tengely”, akkor a lila “referencia szög” vonal (a görbe lila vonal, valamint a terminál oldalán) lett volna levonni az első negyedben.
akárhogy is, a referenciaszög értéke mindig azonos lesz., De ha olyan képet kell rajzolnia, amely megmutatja a referenciaszöget, győződjön meg róla, hogy az osztályához “helyesnek” tekintett helyre rajzolja.
-
keresse meg az 1500°referenciaszögét.
megragadom a számológépemet, és 360° – kal végzem a felosztást “egyszer körül”:
1500 ÷ 360 = 4.16666…
tehát négy ciklus van, plusz egy kicsit. Mennyibe kerül csak a négy ciklus?
4 × 360 = 1440
Ez azt jelenti, hogy a bal oldali rész (a 0,16666… fent) további hatvan fokot jelent., Ez kisebb, mint kilencven fok, így a szög terminális oldala a pozitív y tengelytől jobbra van. Akkor a referencia szög az első negyedben egyenlő:
60°
Tartalom Továbbra is Alul
-
keresse meg az első-kvadránsban referencia szög 954°, valamint a döntetlen mindkét szögek ugyanazon a tengelyen rendszer.
ezt a szöget csökkentem. Hány ciklus illeszkedik ebbe a szögbe?
954 ÷ 360 = 2,65
két ciklus illeszkedik a szögbe., A szög mérésének mekkora részét veszi fel ez a két ciklus?
360 × 2 = 720
akkor mennyi maradt?
954 – 720 = 234
a negatív x-tengely 180°, a negatív y-tengely 270°. Ez a szög az értékek között van, tehát a harmadik kvadránsban van, és a legközelebb lesz a negatív x-tengelyhez.
milyen közel? Ez lesz a távolság a redukált szög és a negatív x-tengely között:
234 – 180 = 54
akkor a referenciaszög:
54°
…,a rajz:
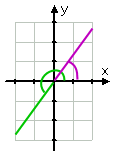
(mivel az eredeti szög, kevesebb, mint két ciklus) zöld, majd rajzoltam az első kvadráns referenciaszöget lila színben. Ha olyan rajzokat készít, amelyek két (vagy több) különálló információt tartalmaznak, hasznos lehet, ha színes ceruza van a kezében. Igen, színes ceruzákat használtam az egyetemen.
-
keresse meg a radiánok referenciaszögét.,
hirdetés
Tehát 0 radián és 2π radián alapján kell gondolkodnom a pozitív x-tengelyre, és π radián a negatív x-tengelyre.
a szög, amit adott nekem
radians. A divízió átalakítani a tört formában, hogy decimális formában (majd figyelmen kívül hagyva a π egyelőre), én:
16 ÷ 5 = 3.2
más szóval,
radián egyenlő 3.2 π radián. Egy ciklus 2π radián, tehát ez egy kicsit több, mint fele-ismét, mint egy ciklus., Más szavakkal, ez a szög kissé meghaladja a negatív x-tengelyt:
3.2 π – 2π = 1.2 π
de milyen messze van a terminál oldala a negatív x-tengelytől?
nem tudok rájönni levonva a szög mértéke a negatív x tengely a csökkentett szög:
1.2 π – 1π
a= 0.2 π
a= (1/5)π
Ez adja a távolságot a terminál oldalán, a (csökkentett) szög, valamint a (negatív) x-tengely radiánban adható meg. A referenciaszög:
-
keresse meg a radiánok referenciaszögét.,
mivel
kevesebb, mint 2, de több , mint, akkor ez a szög a negyedik kvadránsban van, a radiánok és a 2π radiánok között. Akkor a legközelebb van a pozitív x-tengelyhez. De milyen közel? Majd vonjuk ki, hogy megtudja:
Akkor a referencia szög:
– E, hogy dolgozol fok, vagy radiánban adható meg, amíg tudod, a szög intézkedések a pozitív, mind a negatív részeit az x-tengely, csökkentheti a szög (ha szükséges), akkor kivonás, hogy a referencia szög., Ha nem biztos a munkájában, akkor rajzolhatja a képet, hogy biztos legyen benne. De ha még mindig képeket kell rajzolnia, amikor a teszt jön, próbáljon meg néhány extra gyakorlatot elvégezni, mert a teszt azt feltételezi, hogy nincs szüksége időre a képek rajzolásához.
az alábbi Mathway widget segítségével gyakorolhatja a medián megtalálását. Próbálja ki a bevitt gyakorlatot, vagy írja be saját gyakorlatát. Ezután kattintson a gombra, majd válassza a “Find the Reference Angle”, hogy hasonlítsa össze a választ Mathway.,
kérjük, fogadja el a” preferences ” sütiket a widget engedélyezéséhez.
(kattintson a “koppintson a lépések megtekintéséhez” gombra, hogy közvetlenül a Mathway webhelyre kerüljön fizetett frissítéshez.)
URL: https://www.purplemath.com/modules/radians3.htm
1page 2page 3
Leave a Reply