Radiaaneina & DegreesReducing AnglesReference Kulmat
Purplemath
edellisessä jaksossa, löysimme ensimmäisen ympyrän kulma vastineet annetaan kulma toimenpiteitä. Toinen asia, jonka voimme tehdä kulmamittauksilla, jopa ne, joiden toimenpiteet ovat ensimmäisellä kierroksella, on löytää niin sanottu ”referenssikulma”.
vertailukulma on kulma, jonka annettu kulma tekee x-akselilla., Riippumatta siitä, missä kulmassa päät (että on, riippumatta siitä, missä terminaalin puolella kulma), viite kulma toimenpiteet lähin etäisyys, että terminaalin puolella x-akselia.
Sisältö Jatkuu Alla
MathHelp.,com

Kun löytää viite kulmat, se voi olla hyödyllistä pitää mielessä, että positiivinen x-akseli on 0° (360° tai 0 radiaania (ja 2π radiaania); positiivinen y-akseli on 90° tai
radiaaneina; negatiivinen x-akseli on 180° tai π radiaania; ja negatiivinen y-akseli on 270° tai radiaaneina.
aloitetaan helpolla esimerkillä., Kulma, jossa toimenpide 30° olisivat kaavio kuten tämä:
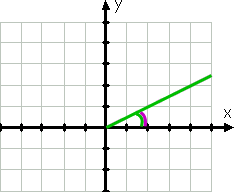
grafiikassa kulma on ensimmäinen puoli on positiivisen x-akselin suuntaan; sen terminaalin puolella on vihreä linja, koska kulmat on piirretty menee vastapäivään. Kaareva vihreä viiva osoittaa annetun kulman.
jo ennen kulman piirtämistä olisin tiennyt, että kulma on ensimmäisessä kvadrantissa, koska 30° on 0° – 90°. Viittaus kulma, näkyy kaareva violetti linja on sama kuin annettu kulma.,
kulma 150°, ilmeisesti, ei ole sama kuin kulma 30°; se on suurempi, ja sen terminaali puolella on toisessa neljänneksessä (koska 150° on välillä 90° ja 180°). Kuitenkin, että terminaalin puolella on vain 30° negatiivinen x-akseli, niin näette violetti viiva piirustus:
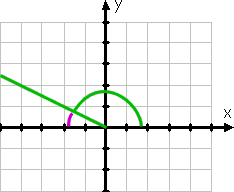
Koska terminaalin puolella 150° on vain kolmekymmentä astetta (negatiivinen) x-akseli (on kolmekymmentä astetta vähemmän kuin 180°, joka on negatiivinen x-akseli), sitten viittaus kulma (taas näkyy kaareva violetti viiva) on 30°.,
jatkaen vastapäivään, voimme kuvittaa 210°. Tämä kulma terminaali puolella, koska 210° on välillä 180° ja 270°, on kolmannessa kvadrantissa, ja tämä puoli on lähinnä negatiivinen x-akseli. Koska 210 on kolmekymmentä yli 180, niin tämä kulma on terminaalin puolella on 30° ohi (eli alla) negatiivisen x-akselin.
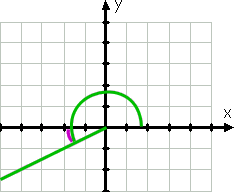
näin Ollen viittaus kulma on 30°.
lyön vetoa, voit arvata, mikä olisi viittaus kulma 330°., Koska 330 on kolmekymmentä vähemmän kuin 360, ja koska 360° = 0°, niin kulma 330° on kolmekymmentä astetta pakkasta (joka on lyhyt) positiivinen x-akseli, neljännessä neljänneksessä. Sen vertailukulma on siis 30°.
Affiliate
Affiliate

Huomaa, miten tämä viimeinen laskenta tehtiin. Minulla ei ollut graafia. Laskin juuri päässäni. Sinun pitäisi piirtää kaavioita niin kauan kuin tarvitset apua, mutta älä pelkää alkaa luottaa aritmeettinen., Kun pääset jyvälle tästä, se on aika suoraviivaista.
Huomautus: Koska viittaus kulma aina toimenpiteet (positiivinen) etäisyys x-akselin, se voidaan nähdä myös olevan ensimmäisen neljänneksen vastaava kulma. Toisin sanoen, kunkin esimerkkejä edellä, jos minun oppikirja määritellään ”viittaus kulma” kuin ”ensimmäisen neljänneksen kulma, jossa sama etäisyys x-akselilla”, sitten violetti ”viittaus kulma” line (kaareva violetti linja, sekä terminaalin puolella) olisi ollut laadittu ensimmäisessä neljänneksessä.
joka tapauksessa referenssikulman arvo on aina sama., Mutta jos sinua pyydetään piirtämään kuva osoittaa viittaus kulma, varmista, että voit kiinnittää sen sijainti, joka on pidetty ”oikean” oman luokan.
-
Etsi vertailukulma 1500°.
otan laskimeni ja tehdä jako 360° ”kun noin”:
1500 ÷ 360 = 4.16666…
joten syklejä on neljä, plus vähän. Paljonko vain neljä sykliä maksaa?
4 × 360 = 1440
Se tarkoittaa, että vasen-yli alkuosa (0.16666… edellä) edustaa toista kuusikymmentä astetta., Tämä on pienempi kuin yhdeksänkymmentä astetta, joten kulman päätepuoli on positiivisen y-akselin oikealla puolella. Sitten viittaus kulma on ensimmäisessä neljänneksessä ja on yhtä suuri kuin:
60°
Sisältö Jatkuu Alla
-
Etsi ensimmäinen-quadrant viite kulma 954°, ja piirtää molemmat kulmat saman akselin järjestelmään.
aloitan vähentämällä tästä kulmasta. Kuinka monta sykliä mahtuu tähän kulmaan?
954 ÷ 360 = 2.65
Kaksi jaksoa mahtuvat kulma., Kuinka paljon kulman mittaa nuo kaksi sykliä vievät?
360 × 2 = 720
paljonko jää yli?
954 – 720 = 234
negatiivinen x-akseli on 180°, ja negatiivinen y-akseli on 270°. Tämä kulma on näiden arvojen välissä, joten se on kolmannessa kvadrantissa ja on lähimpänä negatiivista x-akselia.
kuinka lähellä? Se tulee olemaan etäisyys päätelaitteen puolella vähentää kulma ja negatiivinen x-akseli:
234 – 180 = 54
Sitten viittaus kulma on:
54°
…,ja piirtäminen on:
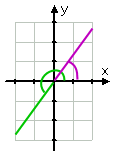
Affiliate
Huomaa, miten piirsin vähentää kulma (joka on alkuperäinen kulma, vähemmän kaksi jaksoa) vihreä, ja sitten piirsin ensimmäisen neljänneksen viite kulma violetti. Kun teet piirustuksia, jotka sisältävät kaksi (tai enemmän) eri paloja tiedot, se voi olla hyödyllistä saada värikynät käsillä. Kyllä, käytin värillisiä lyijykyniä yliopistossa.
-
Etsi viite kulma radiaaneina.,
Mainos
Okei, tämä on radiaaneina. Joten minun täytyy ajatella 0 radiaaneina 2π radiaania positiivinen x-akseli, ja π radiaania negatiivinen x-akseli.
heidän minulle antama kulma on
radiaanit. Tee jako muuntaa murto muodossa desimaalin muodossa (ja unohdetaan π varten hetkellä), en pääse:
16 ÷ 5 = 3.2,
Toisin sanoen,
radiaaneina on yhtä 3.2 π radiaania. Yksi sykli on 2π radiaania, joten tämä on hieman yli puolet-jälleen yhtä paljon kuin yksi sykli., Toisin sanoen, tämä kulma menee vähän ohi negatiivinen x-akseli:
3.2 π – 2π = 1.2 d
Mutta kuinka pitkälle on terminaalin puolella negatiivisen x-akselin?
voin selvittää tämän vähentämällä kulma toimenpide negatiivisen x-akselin minun vähentää kulma:
1.2 g – 1π
= 0.2 π
= (1/5)π
Tämä antaa minulle etäisyys päätelaitteen puolella (alennettu) kulma ja (negatiivinen) x-akselin radiaaneina. Viittaus kulma on:
-
Etsi viite kulma radiaaneina.,
Koska
on vähemmän kuin 2, mutta enemmän kuin , niin tämä kulma on neljännessä quadrant, välillä radiaaneina 2π radiaania. Sitten se on lähimpänä positiivista x-akselia. Mutta kuinka lähellä? Voin vähentää selvittää:
Sitten viittaus kulma on:
Olipa olet työskennellyt asteina tai radiaaneina, niin kauan kuin tiedät kulma toimenpiteiden positiiviset ja negatiiviset osat x-akselin, voit vähentää kulma (jos tarpeen) ja sitten tehdä vähennyksiä saada viittaus kulma., Jos et ole varma työstäsi, voit piirtää kuvan varmaksi. Mutta jos olet vielä tarvitse piirtää kuvia, kun testi on tulossa, kokeile tehdä joitakin ylimääräistä käytännössä, koska testi on menossa olettaa, että sinun ei tarvitse aikaa piirtää kuvia.
voit käyttää alla olevaa Mathway-vekotinta harjoittelemaan mediaanin löytämistä. Kokeile sisään tullutta liikuntaa tai kirjoita omaan liikuntaan. Sitten klikkaa painiketta ja valitse ”Etsi Viite Kulma” verrata vastauksesi Mathway on.,
Please hyväksyä ”asetukset” – evästeet, jotta tämä vekotin.
(klikkaa ”napauta nähdäksesi vaiheet” suoraan Mathway-sivustolle maksullista päivitystä varten.)
URL: https://www.purplemath.com/modules/radians3.htm
Sivu 1Page 2Page 3
Leave a Reply