
Sir Isaac Newton (1643-1727)
en la atmósfera embriagadora de la Inglaterra del siglo XVII, con la expansión del Imperio británico en pleno apogeo, grandes universidades antiguas como Oxford y Cambridge estaban produciendo muchos grandes científicos y matemáticos. Pero el más grande de todos fue sin duda Sir Isaac Newton.,
físico, matemático, astrónomo, filósofo natural, alquimista y teólogo, Newton es considerado por muchos como uno de los hombres más influyentes en la historia humana. Su publicación de 1687, la «Philosophiae Naturalis Principia Mathematica «(generalmente llamada simplemente» Principia»), es considerada como uno de los libros más influyentes en la historia de la ciencia, y dominó la visión científica del universo físico durante los siguientes tres siglos.,
aunque en gran medida sinónimo en la mente del público en general hoy en día con la gravedad y la historia del manzano, Newton sigue siendo un gigante en la mente de los matemáticos de todo el mundo (a la par con los grandes de todos los tiempos como Arquímedes y Gauss), e influyó en gran medida el camino posterior del desarrollo matemático.
durante dos años milagrosos, durante la época de la gran plaga de 1665-6, el joven Newton desarrolló una nueva teoría de la luz, descubrió y cuantificó la gravitación, y fue pionero en un nuevo enfoque revolucionario de las matemáticas: el cálculo infinitesimal., Su teoría del cálculo se basó en el trabajo anterior de sus compañeros ingleses John Wallis e Isaac Barrow, así como en el trabajo de matemáticos continentales como René Descartes, Pierre de Fermat, Bonaventura Cavalieri, Johann van Waveren Hudde y Gilles Personne de Roberval. A diferencia de la geometría estática de los griegos, el cálculo permitió a los matemáticos e ingenieros dar sentido al movimiento y al cambio dinámico en el mundo cambiante que nos rodea, como las órbitas de los planetas, el movimiento de los fluidos, etc.,
la pendiente media de una curva
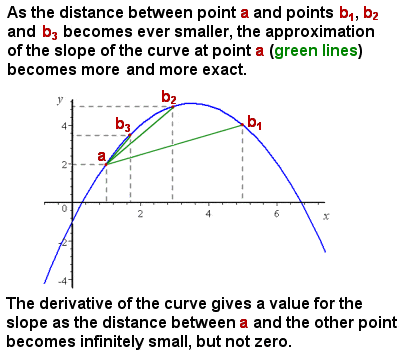
La diferenciación (derivada) se aproxima a la pendiente de una curva a medida que el intervalo se acerca a cero
el problema inicial que Newton enfrentaba era que, aunque era bastante fácil representar y calcular la pendiente media de una curva (por ejemplo, la velocidad creciente de un objeto en un gráfico de tiempo-distancia), la pendiente de una curva variaba constantemente, y no había ningún método para dar la pendiente exacta en cualquier punto individual de la curva, es decir., efectivamente la pendiente de una recta tangente a la curva en ese punto.
intuitivamente, la pendiente en un punto en particular se puede aproximar tomando la pendiente promedio («rise over run») de segmentos cada vez más pequeños de la curva. A medida que el segmento de la curva que se considera se acerca a cero en tamaño (es decir, un cambio infinitesimal en x), entonces el cálculo de la pendiente se acerca cada vez más a la pendiente exacta en un punto (Ver imagen a la derecha).,
sin entrar en demasiados detalles complicados, Newton(y su contemporáneo Gottfried Leibniz independientemente) calculó una función derivada f ‘(x) que da la pendiente en cualquier punto de una función f (x). Este proceso de calcular la pendiente o derivada de una curva o función se llama cálculo diferencial o diferenciación (o, en la terminología de Newton, el «método de fluxiones» – él llamó a la tasa instantánea de cambio en un punto particular en una curva el «fluxión», y los valores cambiantes de x E y los «fluentes»)., Por ejemplo, la derivada de una recta del tipo f ( x) = 4x es solo 4; la derivada de una función cuadrada f(x) = x2 es 2x; la derivada de la función cúbica f(x) = x3 es 3×2, etc. Generalizando, la derivada de cualquier función de potencia f (x) = xr es rxr-1. Otras funciones derivadas se pueden indicar, de acuerdo con ciertas reglas, para funciones exponenciales y logarítmicas, funciones trigonométricas como sin(x), cos (x), etc., de modo que una función derivada se puede indicar para cualquier curva sin discontinuidades., Por ejemplo, la derivada de la curva f ( x) = x4 – 5×3 + sin(x2) sería f ‘(x) = 4×3 – 15×2 + 2xcos(x2).
habiendo establecido la función derivada para una curva particular, entonces es fácil calcular la pendiente en cualquier punto particular de esa curva, simplemente insertando un valor para x. en el caso de un gráfico de tiempo-distancia, por ejemplo, esta pendiente representa la velocidad del objeto en un punto particular.,
método de fluidos
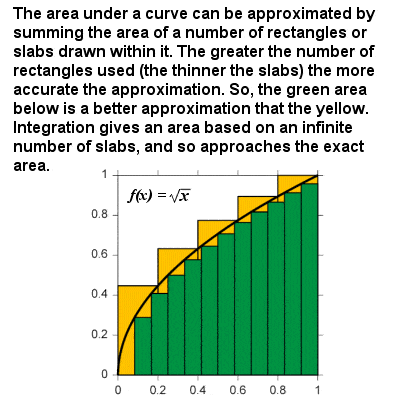
La integración se aproxima al área bajo una curva a medida que el tamaño de las muestras se aproxima a cero
El «opuesto» de diferenciación es la integración o cálculo integral (o, en la terminología de Newton, el «método de fluidos»), y juntos la diferenciación y la integración son las dos operaciones principales del cálculo., El Teorema Fundamental del cálculo de Newton establece que la diferenciación y la integración son operaciones inversas, de modo que, si una función se integra primero y luego se diferencia (o viceversa), se recupera la función original.
la integral de una curva puede considerarse como la fórmula para calcular el área limitada por la curva y el eje x entre dos límites definidos. Por ejemplo, en un gráfico de velocidad contra el tiempo, el área «bajo la curva» representaría la distancia recorrida., Esencialmente, la integración se basa en un procedimiento limitante que se aproxima al área de una región curvilínea al romperla en losas verticales o columnas infinitesimalmente delgadas. De la misma manera que para la diferenciación, una función integral se puede establecer en términos generales: la integral de cualquier potencia f(x) = xr es xr+1⁄r+1, y hay otras funciones integrales para funciones exponenciales y logarítmicas, funciones trigonométricas, etc., de modo que el área bajo cualquier curva continua se puede obtener entre dos límites cualesquiera.,
Newton optó por no publicar sus matemáticas revolucionarias de inmediato, preocupado por ser ridiculizado por sus ideas no convencionales, y se contentó con Circular sus pensamientos entre amigos. Después de todo, tenía muchos otros intereses como la filosofía, la alquimia y su trabajo en la Casa De La Moneda Real. Sin embargo, en 1684, el alemán Leibniz publicó su propia versión independiente de la teoría, mientras que Newton No publicó nada sobre el tema hasta 1693., Aunque la Royal Society, después de la debida deliberación, dio crédito por el primer descubrimiento a Newton (y el crédito por la primera publicación a Leibniz), algo de escándalo surgió cuando se hizo público que la acusación posterior de la Royal Society de plagio contra Leibniz fue en realidad escrita por ningún otro Newton mismo, causando una controversia en curso que empañó las carreras de ambos hombres.,
teorema binomial generalizado
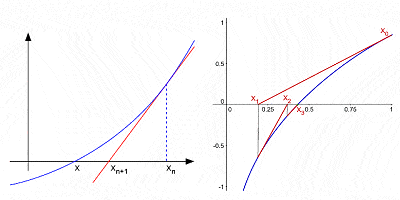
El Método de Newton para aproximar las raíces de una curva por interaciones sucesivas después de una suposición inicial
A pesar de ser de lejos su contribución más conocida a las matemáticas, el cálculo no fue de ninguna manera la única contribución de Newton.,Raic expansión de los poderes de un binomio (una expresión algebraica con dos términos, tales como a2 – b2); hizo contribuciones sustanciales a la teoría de las diferencias finitas (expresiones matemáticas de la forma f(x + b) – f(x + a)); fue uno de los primeros en utilizar exponentes fraccionados y geometría de coordenadas para derivar soluciones a ecuaciones diofánticas (ecuaciones algebraicas con variables de solo entero); desarrolló el llamado «método de Newton» para encontrar sucesivamente mejores aproximaciones a los ceros o raíces de una función; desarrolló fue el PRIMERO en usar series de potencia infinita con cualquier confianza; etc.,
en 1687, Newton publicó su «Principia» o «los principios matemáticos de la filosofía Natural», generalmente reconocido como el libro científico más grande jamás escrito. En él, presentó sus teorías del movimiento, la gravedad y la mecánica, explicó las órbitas excéntricas de los cometas, las mareas y sus variaciones, la precesión del eje de la Tierra y el movimiento de la Luna.,
Más tarde en la vida, escribió una serie de tratados religiosos que tratan de la interpretación literal de la Biblia, dedicó una gran cantidad de tiempo a la alquimia, actuó como miembro del Parlamento durante algunos años, y se convirtió quizás en el maestro más conocido de la casa de la moneda real en 1699, una posición que mantuvo hasta su muerte en 1727. En 1703, fue nombrado Presidente de la Royal Society y, en 1705, se convirtió en el primer científico en ser nombrado caballero. El envenenamiento por mercurio de sus actividades alquímicas quizás explicó la excentricidad de Newton en su vida posterior, y posiblemente también su muerte eventual.,
| << Back to Pascal | Forward to Leibniz >> |
Leave a Reply