
Statistiky jsou uspořádání statistických testů, které analytici používají k dělat závěr z uvedené údaje. Tyto testy nám umožňují rozhodovat na základě pozorovaného vzoru z dat. Existuje široký rozsah statistických testů. Výběr, který statistický test použít, závisí na struktuře dat, distribuci dat a variabilním typu.,Existuje mnoho různých typů testů ve statistikách, jako je T-test, Z-test, chi-square test, ANOVA test, binomický test, jeden vzorek střední test atd.
volba statistického testu –
parametrické testy se používají, pokud jsou data normálně distribuována .Parametrický statistický test předpokládá parametry populace a rozdělení, ze kterých data pocházejí. Tyto typy testů zahrnují t-testy, z-testy a ANOVA testy, které předpokládají, že data jsou z normální distribuce.,
z-test-z-test je statistický test používaný k určení, zda jsou dva populační prostředky odlišné, pokud jsou známy odchylky a velikost vzorku je velká. V z-testu se porovnává průměr populace.Použitými parametry jsou průměr populace a směrodatná odchylka populace. Z-test se používá k ověření hypotézy, že odebraný vzorek patří do stejné populace.,
Ho: výběrový průměr je stejný jako průměr populace(Nulová hypotéza)
Ha: výběrový průměr je stejný jako průměr populace(Alternativní hypotéza)
z = (x — μ) / (σ / √n),
, kde x=výběrový průměr, u=populační průměr, σ / √n = směrodatná odchylka.
Pokud je hodnota z menší než kritická hodnota, přijměte nulovou hypotézu jinak odmítněte nulovou hypotézu.
t-test-In t-test průměr obou daných vzorků se porovnává. T-test se používá, pokud nejsou známy parametry populace (střední a směrodatná odchylka).,
spárované testy t-testu na rozdíl mezi dvěma proměnnými ze stejné populace (skóre před a po testu). Například-v tréninkovém programu výkonnostní skóre stážisty před a po dokončení programu.
Nezávislý T-test – nezávislý t-test, který je také volal dva ukázkové t-test nebo studentův t-test je statistický test, který určuje, zda existuje statisticky významný rozdíl mezi průměry ve dvou nezávislých skupinách.Například-porovnávání chlapců a dívek v populaci.,
jeden vzorek t-test-průměr jedné skupiny se porovnává s daným průměrem. Například-zkontrolovat zvýšení a snížení prodeje, pokud je uveden průměrný prodej.
t = (x1-x2) / (σ / √n1 + σ/√n2),
kde x1 a x2 jsou průměr vzorku 1 a vzorku 2.
Anova Test-analýza rozptylu (ANOVA) je statistická technika, která se používá ke kontrole, zda se prostředky dvou nebo více skupin výrazně liší od sebe. ANOVA kontroluje dopad jednoho nebo více faktorů porovnáním prostředků různých vzorků., Pokud použijeme t-test místo ANOVA testu, nebude spolehlivý, protože počet vzorků je více než dva a ve výsledku to způsobí chybu.
hypotéza testovaná v Anově je
Ho: všechny páry vzorků jsou stejné, tj., všech výběrových průměrů se rovná
Ha: alespoň jedna dvojice vzorků se výrazně liší
V anova testu můžeme vypočítat F hodnotu a porovnat ji s kritickou hodnotou
F= ((SSE1 — SSE2)/m)/ SSE2/n-k, kde
SSE = reziduální součet čtverců
m = počet omezení,
k = počet nezávislých proměnných,
neparametrický statistický test – neparametrický testy se používají, pokud data nejsou normálně rozložena. Neparametrické testy zahrnují chi-čtvercový test.
Chi-square test (χ2 test) – chi-square test se používá k porovnání dvou kategorických proměnných., Výpočet statistické hodnoty Chi-Square a jeho porovnání s kritickou hodnotou z distribuce Chi-Square umožňuje posoudit, zda se pozorovaná frekvence výrazně liší od očekávané frekvence.
testovaná hypotéza pro chi-square je –
Ho: proměnná x a proměnná y jsou nezávislé
Ha: proměnná x a proměnná y nejsou nezávislé.,
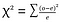
where o=observed , e=expected.
Leave a Reply