ISAAC NEWTON: Matematika A diferenciální počet

Sir Isaac Newton (1643-1727)

V opojné atmosféře 17. Století v Anglii, s expanzí Britského impéria v plném proudu, grand old univerzit, jako je Oxford a Cambridge byly produkuje mnoho skvělých vědců a matematiků. Ale největší z nich byl nepochybně Sir Isaac Newton.,

fyzik, matematik, astronom, přírodní filozof, alchymista a teolog, Newton je mnohými považován za jednoho z nejvlivnějších mužů v lidské historii. Jeho 1687 zveřejnění, „Philosophiae Naturalis Principia Mathematica“ (obvykle nazvaný jednoduše „Principia“), je považována za jednu z nejvlivnějších knih v historii vědy, a to ovládal vědeckého pohledu na fyzický svět pro další tři století.,

i když do značné míry synonymem v myslích široké veřejnosti dnes s gravitací a příběh jabloň, Newton zůstává obří v myslích matematici všude (na stejné úrovni s all-time velikáni jako Archimedes a Gauss), a on výrazně ovlivnil následné cestě matematický vývoj.

Více než dvě zázračné let, v době Velkého Moru z 1665-6, mladý Newton vyvinul novou teorii světla, objevil a kvantifikovat gravitace, a propagoval revoluční nový přístup k matematice: infinitezimální kalkul., Jeho teorie kalkul postavený na starší práce jeho kolegy Angličané John Wallis a Isaac Barrow, stejně jako na práci jako Kontinentální matematiky, jako René Descartes, Pierre de Fermat, Bonaventura Cavalieri, Johann van Waveren Hudde a Gilles Personne de Roberval. Na rozdíl od statické geometrie Řeků, počet povoleno matematiků a inženýrů, aby se smysl pohybu a dynamické změny v měnícím se světě kolem nás, jako jsou oběžné dráhy planet, pohybu, tekutin, atd.,

Průměrný Sklon této Křivky

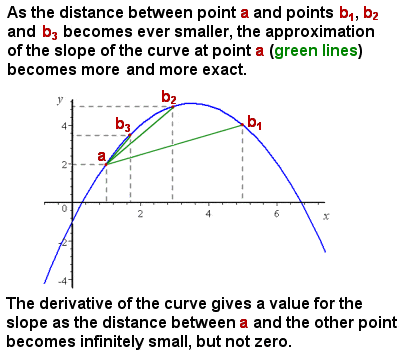
Diferenciace (derivace) aproximuje sklon křivky jako interval blíží k nule,

původní problém byl Newton konfrontace bylo, že i když to bylo dost snadné se představují a vypočítat průměrný sklon křivky (např. zvyšující se rychlost objektu, na čas-vzdálenost graf), že sklon této křivky se neustále proměnlivé, a tam byl žádný způsob, jak dát přesné svahu na jeden konkrétní bod na křivce, tj., účinně sklon tečné čáry ke křivce v tomto bodě.

intuitivně lze sklon v určitém bodě aproximovat tím, že vezmeme průměrný sklon („rise over run“) stále menších segmentů křivky. Jako segment křivky uvažuje se blíží k nule ve velikosti (tj. nekonečně malá změna v x), pak výpočet svahu blíží blíž a blíž k přesné sklon v bodě (viz obrázek vpravo).,

Aniž bychom se pouštěli do příliš složitý detail, Newton (a jeho současník Gottfried Leibniz nezávisle na sobě) vypočítá derivaci funkce f ‚(x), která dává sklon v libovolném bodě funkce f(x). Tento proces výpočtu sklonu nebo derivace křivky nebo funkce je tzv. diferenciální kalkul, nebo diferenciaci (nebo Newtonova terminologie, „metoda fluxions“ – on nazývá okamžitá rychlost změny na konkrétní bod na křivce „fluxion“, a měnící se hodnoty x a y „fluents“)., Například, derivát přímky typu f(x) = 4x je jen 4; derivace druhou funkci f(x) = x2 je 2x, derivace kubické funkce f(x) = x3 je 3×2, atd. Zobecnění, derivace jakékoli výkonové funkce f (x) = xr je rxr-1. Druhé derivace funkce může být uvedeno, podle určitých pravidel, pro exponenciální a logaritmické funkce, goniometrické funkce jako sin(x), cos(x), atd., tak, že derivace funkce může být uvedeno pro každou křivku bez nespojitostí., Například derivace křivky f(x) = x4 – 5×3 + sin(x2) by byla f ‚(x) = 4×3 – 15×2 + 2xcos (x2).

po zjištění derivace funkce pro konkrétní křivky, to je pak snadná záležitost calcuate sklon v jakémkoli bodě na této křivce, jen vložením hodnoty pro x. V případě, že čas-vzdálenost graf, například, tento sklon představuje rychlost objektu v určitém bodě.,

Metoda Fluents

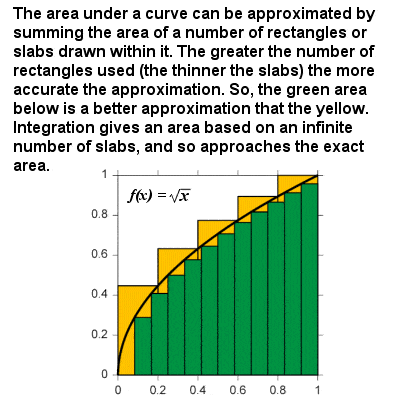
Integrace aproximuje plochu pod křivkou jako velikost vzorků se blíží k nule

„opačné“ diferenciace je integrace a integrální počet (nebo Newtonova terminologii, „metoda fluents“), a spolu diferenciace a integrace jsou dvě hlavní operace kalkulu., Newton je Základní Věta Kalkulu uvádí, že diferenciace a integrace jsou inverzní operace, tak, že, pokud funkce je první integrované a pak diferencované (nebo naopak), původní funkce je načtena.

integrál křivky lze považovat za vzorec pro výpočet plochy ohraničené křivkou a osou x mezi dvěma definovanými hranicemi. Například na grafu rychlosti proti času by oblast „pod křivkou“ představovala ujetou vzdálenost., Integrace je v podstatě založena na omezujícím postupu, který přibližuje oblast křivočaré oblasti tím, že ji rozdělí na nekonečně tenké svislé desky nebo sloupy. Stejným způsobem jako pro diferenciaci, integrální funkce může být uvedeno v obecné pojmy: integrál z nějaké síly f(x) = xr je xr+1⁄r+1, a tam jsou jiné integrál funkce pro exponenciální a logaritmické funkce, goniometrické funkce, atd., tak, aby oblast pod jakoukoli spojitou křivku lze získat mezi dvěma limity.,

Newton rozhodl zveřejnit jeho revoluční matematika ihned, obávají zesměšňován pro jeho nekonvenční nápady, a spokojil se s cirkulující jeho myšlenky mezi přáteli. Koneckonců, měl mnoho dalších zájmů, jako je filozofie, alchymie a jeho práce v královské mincovně. Nicméně, v roce 1684, německý Leibniz publikoval jeho vlastní nezávislou verzi teorie, zatímco Newton publikoval nic na toto téma až do roku 1693., I když Královské Společnosti, po zralé úvaze, dal kredit za první objev Newton (a kredit za první zveřejnění Leibniz), něco jako skandál vznikl, když bylo zveřejněno, že Královské Společnosti je následné obvinění z plagiátorství proti Leibniz byl vlastně autorem není nikdo jiný Newton sám, což způsobuje probíhající diskuse, které zmařily kariéry obou mužů.,

Zobecněná Binomická Věta

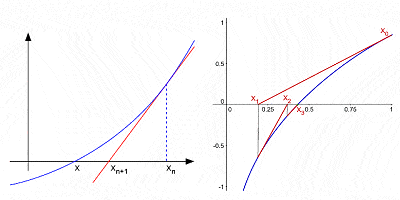
Newtonova Metoda pro sbližování kořeny křivky postupným interations po počáteční odhad

Přesto, že zdaleka jeho nejznámější příspěvek k matematice, kalkul byl v žádném případě Newton je jen příspěvek.,raic rozšíření pravomocí binomické (algebraický výraz s dvěma termíny, jako a2 – b2); on učinil významné příspěvky k teorii konečných rozdílů (matematické vyjádření tvaru f(x + b) – f(x + a)); byl jeden z prvních používat zlomkové exponenty a koordinovat geometrie odvodit řešení Diophantine rovnic (algebraické rovnice s celočíselnými-pouze proměnné); on vyvinul takzvanou „newtonovu metodu“ pro nalezení postupně lepší aproximace nuly nebo kořeny funkce; on byl první používat nekonečné mocninné řady s jistotou; atd.,

V roce 1687 Newton publikoval jeho „Principia“ nebo „Matematické Principy Přírodní Filozofie“, obecně uznávány jako nejlepší vědecké knihy kdy byla napsána. V něm představil své teorie pohybu, gravitace a mechaniky, vysvětlil excentrické oběžné dráhy komet, přílivy a jejich variace, precesi zemské osy a pohyb Měsíce.,

Později v životě, napsal řadu náboženských traktátů zabývajících se doslovný výklad Bible, věnoval mnoho času alchymii, působil jako Člen Parlamentu po několik let, a stal se možná best-known Mistr Královské Mincovny, v roce 1699, pozici zastával až do své smrti v roce 1727. V roce 1703 byl prezidentem Královské společnosti a v roce 1705 se stal prvním vědcem, který kdy byl rytířem. Otrava rtutí z jeho alchymických pronásledování možná vysvětlila Newtonovu excentricitu v pozdějším životě a možná i jeho případnou smrt.,