
Statistiken sind die Anordnung statistischer Tests, mit denen Analysten aus die angegebenen Daten. Diese Tests ermöglichen es uns, Entscheidungen auf der Grundlage beobachteter Muster aus Daten zu treffen. Es gibt ein breites Spektrum statistischer Tests. Die Wahl des zu verwendenden statistischen Tests hängt von der Struktur der Daten, der Verteilung der Daten und dem Variablentyp ab.,Es gibt viele verschiedene Arten von Tests in Statistiken wie T-Test, Z-Test, Chi-Quadrat-Test ,Anova-Test, Binomialtest, ein Beispiel-Median-Test usw.
Auswahl eines statistischen Tests –
Parametrische Tests werden verwendet, wenn die Daten normal verteilt sind .Ein parametrischer statistischer Test macht eine Annahme über die Populationsparameter und die Verteilungen, aus denen die Daten stammen. Diese Testtypen umfassen T-Tests, Z-Tests und Anova-Tests, bei denen davon ausgegangen wird, dass die Daten normal verteilt sind.,
Z-test-Ein z-Test ist ein statistischer Test, der verwendet wird, um zu bestimmen, ob zwei Populationsmittel unterschiedlich sind, wenn die Varianzen bekannt sind und die Stichprobengröße groß ist. Im z-Test wird der Mittelwert der Population verglichen.Die verwendeten Parameter sind Populationsmittel und Populationsstandardabweichung. Z-Test wird verwendet, um eine Hypothese zu validieren, dass die gezogene Stichprobe zur gleichen Population gehört.,
Ho: Stichprobenmittelwert ist derselbe wie der Grundgesamtmittelwert(Nullhypothese)
Ha: Stichprobenmittelwert ist nicht derselbe wie der Grundgesamtmittelwert (Alternative Hypothese)
z = (x — μ) / (σ / √n),
wobei x=Stichprobenmittelwert , u=Grundgesamtmittelwert, σ / √n = Grundgesamtstandardabweichung ist.
Wenn der z-Wert kleiner als der kritische Wert ist, akzeptieren Sie die Nullhypothese andernfalls lehnen Sie die Nullhypothese ab.
T-Test-Im t-Test wird der Mittelwert der beiden gegebenen Proben verglichen. Ein t-Test wird verwendet, wenn die Grundgesamtparameter (Mittelwert und Standardabweichung) nicht bekannt sind.,
Gepaart T-Test-Tests für die Differenz zwischen zwei Variablen aus der gleichen Population (Pre – und Post-Test-Score). Zum Beispiel – In einem Trainingsprogramm Leistungsbewertung des Auszubildenden vor und nach Abschluss des Programms.
Unabhängiger T-Test-Der unabhängige T-Test, der auch als Zwei-Probe-T-Test oder Schüler-T-Test bezeichnet wird, ist ein statistischer Test, der bestimmt, ob es einen statistisch signifikanten Unterschied zwischen den Mitteln in zwei unabhängigen Gruppen gibt.Zum Beispiel-Vergleich von Jungen und Mädchen in einer Bevölkerung.,
Ein Beispiel-t-Test – Der Mittelwert einer einzelnen Gruppe wird mit einem gegebenen Mittelwert verglichen. Zum Beispiel-um die Zunahme und Abnahme des Umsatzes zu überprüfen, wenn der durchschnittliche Umsatz angegeben wird.
t = (x1 — x2) / (σ / √n1 + σ / √n2),
wobei x1 und x2 Mittelwert von Probe 1 bzw.
ANOVA-Test – Varianzanalyse (ANOVA) ist eine statistische Technik, mit der überprüft wird, ob sich die Mittelwerte von zwei oder mehr Gruppen signifikant voneinander unterscheiden. ANOVA prüft die Auswirkungen eines oder mehrerer Faktoren durch Vergleich der Mittel verschiedener Stichproben., Wenn wir einen T-Test anstelle von ANOVA-Test verwenden, ist dies nicht zuverlässig, da die Anzahl der Stichproben mehr als zwei beträgt und das Ergebnis fehlerhaft ist.
Die Hypothese, die in ANOVA getestet wird, ist
Ho: Alle Probenpaare sind gleich, dh, alle Stichprobenmittelwerte sind gleich
Ha: Mindestens ein Stichprobenpaar unterscheidet sich signifikant
Im Anova — Test berechnen wir den F-Wert und vergleichen ihn mit dem kritischen Wert
F= ((SSE1 – SSE2)/m)/ SSE2/n-k, wobei
SSE = Restsumme der Quadrate
m = Anzahl der Einschränkungen
k = Anzahl der unabhängigen Variablen
Nicht Parametrischer statistischer Test-Nicht parametrische Tests werden verwendet, wenn Daten normalerweise nicht verteilt sind. Nicht parametrische Tests umfassen Chi-Quadrat-Test.
Chi-Quadrat-Test (χ2-Test)-chi-Quadrat-Test wird verwendet, um zwei kategoriale Variablen zu vergleichen., Durch die Berechnung des Chi-Quadrat-Statistikwerts und den Vergleich mit einem kritischen Wert aus der Chi-Quadrat-Verteilung kann beurteilt werden, ob sich die beobachtete Frequenz signifikant von der erwarteten Frequenz unterscheidet.
Die Hypothese, die für chi-Quadrat getestet wird, ist –
Ho: Variable x und Variable y sind unabhängig
Ha: Variable x und Variable y sind nicht unabhängig.,
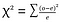
where o=observed , e=expected.
Leave a Reply