
Statistikk er arrangement av statistiske tester som analytikere bruker for å gjøre slutning ut fra de data som er gitt. Disse testene gjør oss i stand til å ta beslutninger på grunnlag av observert mønster fra data. Det er et bredt rangeof statistiske tester. Valget av hvilke statistiske tester for å utnytte baserer seg på strukturen av data, distribusjon av data, og variabeltype.,Det er mange forskjellige typer tester i statistikk som t-test,Z-test,chi-square tester, anova test ,binomial test, ett eksempel median test etc.
Velge en Statistisk test-
Parametriske tester brukes hvis dataene er normalfordelt .En parametrisk statistiske tester gjør en antakelse om befolkningen parametere og distribusjoner at dataene kom fra. Disse typer test inkluderer t-tester,z-tester og anova tester, som antar data er fra normal distribusjon.,
Z-test – En z-test er en statistisk test som brukes til å avgjøre om to populasjonsgjennomsnitt er forskjellige når avvik er kjent og sample størrelse er stor. I z-test gjennomsnittet av populasjonen som er sammenlignet.Parametrene som brukes er populasjonsgjennomsnittet og standardavviket. Z-test brukes for å bekrefte en hypotese om at utvalget trukket tilhører samme bestand.,
Ho: Eksempel mener er de samme som populasjonsgjennomsnittet(nullhypotesen)
Ha: utvalgsgjennomsnitt er ikke samme som populasjonsgjennomsnittet(Alternativ hypotese)
z = (x — μ) / (σ / √n)
der x=utvalgsgjennomsnittet, u=populasjonsgjennomsnitt, σ / √n = standardavviket.
Hvis z-verdien er mindre enn kritisk verdi akseptere nullhypotesen annet avvise nullhypotesen.
T-test t-test for gjennomsnittet av de to prøvene er gitt forhold. En t-test er brukt når befolkningen parametre (gjennomsnitt og standardavvik) er ikke kjent.,
Parede T-Tester-Tester for forskjellen mellom to variabler fra den samme populasjonen( pre – og post test score). For eksempel – I et treningsprogram ytelse resultat av trainee før og etter gjennomføringen av programmet.
Uavhengig T-test – uavhengig t-test, som også kalles to-utvalg t-test eller student ‘ s t-test, er en statistisk test som avgjør om det er en statistisk signifikant forskjell mellom gjennomsnittene i to urelaterte grupper.For eksempel sammenligne gutter og jenter i en befolkning.,
Ett eksempel t-test – middelverdien av en enkelt gruppe er sammenlignet med en gitt bety. For eksempel-for å sjekke økning og nedgang i salg hvis den gjennomsnittlige omsetningen er gitt.
t = (x1 — x2) / (σ / √n1 + σ / √n2),
der x1 og x2 er gjennomsnitt for utvalg 1 og utvalg 2 henholdsvis.
ANOVA Test – Analyse av varians (ANOVA) er en statistisk teknikk som brukes til å sjekke om det betyr at av to eller flere av gruppene er signifikant forskjellige fra hverandre. ANOVA kontrollerer virkningen av en eller flere faktorer ved å sammenligne hjelp av ulike prøver., Hvis vi bruker en t-test i stedet for ANOVA test det vil ikke være pålitelig som antall prøver er mer enn to og det vil gi feil resultat.
Den hypotesen som skal testes i ANOVA er
Ho: Alle par av prøvene er samme dvs., alle eksempel betyr er lik
Ha: minst ett par av prøvene er vesentlig forskjellig
I anova-testen vi beregner F-verdi og sammenligne den med kritisk verdi
F= ((SSE1 — SSE2)/m)/ SSE2/n-k, hvor
SSE = residual sum of squares
m = antall restriksjoner
k = antall uavhengige variabler
Ikke-parametrisk statistiske testen – Ikke-parametriske tester brukes når data er ikke normalfordelt. Ikke-parametriske testene inkluderer chi-kvadrat-test.
Chi-square test( χ2-test)- chi-kvadrat-test er brukt for å sammenligne to kategoriske variabler., Beregning av Chi-Kvadrat statistikk verdi og sammenligne den mot en kritisk verdi fra Chi-Kvadrat fordeling gjør det mulig å vurdere om den observerte frekvensen er vesentlig forskjellig fra den forventede frekvensen.
hypotesen testes for chi-square-
Ho: Variabel x og Variabel y er uavhengige
Ha: Variabel x og Variabel y er ikke uavhengige.,
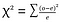
where o=observed , e=expected.
Leave a Reply