
Sir Isaac Newton (1643-1727)
I den berusende atmosfæren i det 17. Århundre England, med utvidelsen av det Britiske imperiet i full gang, grand old universiteter som Oxford og Cambridge var å produsere mange flotte forskere og matematikere. Men den største av dem alle var utvilsomt Sir Isaac Newton.,
Fysiker, matematiker, astronom, naturfilosofen, alchemist, og teolog, Newton er av mange ansett for å være en av de mest innflytelsesrike mennene i menneskehetens historie. Hans 1687 publikasjonen, «Philosophiae Naturalis Principia Mathematica» (vanligvis kalt bare «Principia»), er ansett å være blant de mest innflytelsesrike bøker i vitenskapens historie, og det dominerte den vitenskapelige oppfatning av det fysiske universet for de neste tre århundrer.,
Selv om det i stor grad synonymt i hodet av allmennheten i dag med tyngdekraften og historien om apple tree, Newton er fortsatt en gigant i hodet av matematikere overalt (på lik linje med tidenes storheter som Arkimedes og Gauss), og han sterkt påvirket av den etterfølgende banen av matematiske utvikling.
Over to mirakuløse år, i løpet av den Store Pesten i 1665-6, unge Newton utviklet en ny teori om lys, oppdaget og kvantifiseres gravitasjon, og utviklet en ny, revolusjonerende tilnærming til matematikk: uendelige lite kalkulus., Hans teori om matematisk analyse bygget på tidligere arbeid av hans andre Engelskmenn John Wallis og Isaac Barrow, samt på verk av slike Kontinental matematikere som René Descartes, Pierre de Fermat’, Bonaventura Cavalieri, Johann van Waveren Hudde og Gilles Personne de Roberval. I motsetning til den statiske geometri av Grekerne, kalkulus tillatt matematikere og ingeniører til å gjøre følelse av bevegelse og dynamisk endring i den endrede verden rundt oss, for eksempel banene til planetene, bevegelse av væsker osv.,
Den Gjennomsnittlige Helling av en Kurve
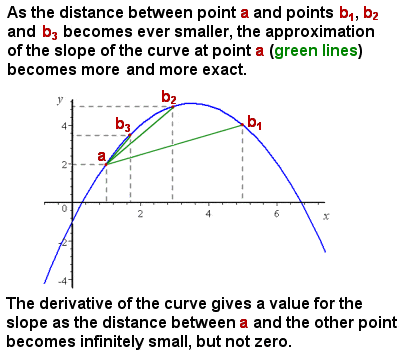
Differensiering (derivater) er tilnærmet lik helningen på kurven intervallet nærmer seg null
Den første problemet Newton var å konfrontere var at, selv om det var lett nok til å representere og beregne den gjennomsnittlige helling av en kurve (for eksempel det øker hastigheten til et objekt på en gang-avstand grafen), skråningen av en kurve ble stadig varierende, og det var ingen metode til å gi den eksakte skråningen på ett enkelt punkt i kurven, dvs., effektivt skråningen av en tangentlinje til kurven på det tidspunktet.
Intuitivt, skråningen på et bestemt tidspunkt kan oppnå ved å ta gjennomsnittet skråningen («stige over kjøre») av stadig mindre segmenter av kurven. Som den delen av kurven som blir ansett som nærmer seg null i størrelse (dvs. et uendelige lite endring i x), deretter beregning av skråningen tilnærminger nærmere og nærmere den eksakte skråningen i et punkt (se bilde til høyre).,
Uten å gå i for mye komplisert detalj, Newton (og hans samtidige Gottfried Leibniz uavhengig) beregnet et derivat funksjonen f ‘(x) som gir skråningen på noe punkt av en funksjon f(x). Denne prosessen med beregning av skråningen eller derivat av en kurve eller funksjonen kalles differensiell kalkulus eller differensiering (eller, i Newton ‘ s terminologi, «metode for fluxions» – han ringte øyeblikkelig endring på et bestemt punkt på en kurve «flyteteksturer», og endre verdiene av x og y «fluents»)., For eksempel, den deriverte av en rett linje av typen f(x) = 4x ligger bare 4; den deriverte av en kvadratisk funksjon f(x) = x2 er 2x; den deriverte av kubikk funksjonen f(x) = x3 er 3×2, etc. Generaliseringen, den deriverte av noen makt funksjonen f(x) = xr er rxr-1. Andre derivater funksjoner kan være oppgitt, i henhold til visse regler, for eksponential-og logaritmefunksjoner, trigonometriske funksjoner, som for eksempel sin(x), cos(x), etc, slik at et derivat-funksjonen kan angis for alle kurve uten discontinuities., For eksempel, den deriverte av kurven f(x) = x4 – 5×3 + sin(x2) ville være f ‘(x) = 4×3 – 15×2 + 2xcos(x2).
etter å Ha etablert den deriverte funksjonen for en bestemt kurve, det er da en enkel sak å calcuate skråningen på et bestemt punkt på kurven, bare ved å sette inn en verdi for x. I tilfelle av en gang-avstand grafen, for eksempel, denne skråningen representerer hastigheten på objektet ved et bestemt punkt.,
Metode for Fluents
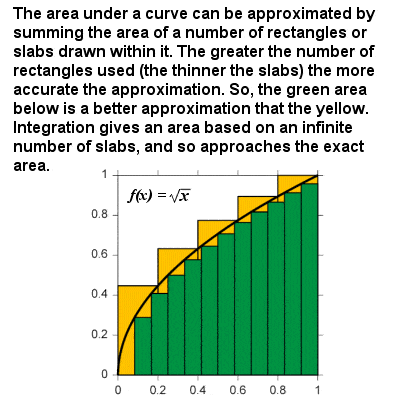
Integrering er tilnærmet lik arealet under en kurve som størrelsen av prøvene nærmer seg null
Den «motsatte» av differensiering er integrering eller integrert kalkulus (eller, i Newton ‘ s terminologi, «metode for fluents»), og sammen differensiering og integrering er to av de viktigste drift av kalkulus., Newton ‘ s Fundamental Teorem av Kalkulus sier at differensiering og integrering er invers operasjoner, slik at hvis en funksjon er første integrerte og deretter differensiert (eller vice versa), den opprinnelige funksjonen er hentet.
integralet av en kurve kan være tenkt som formelen for beregning av området avgrenset av kurven og x-aksen mellom to definerte grenser. For eksempel, på en graf av hastighet i forhold til tid, området under kurven» ville representere avstanden reiste., I hovedsak, integrering er basert på en begrensende prosedyre som tilsvarer arealet av en kurvelineær regionen ved å bryte det i infinitesimally tynne vertikale plater eller kolonner. På samme måte som for differensiering, og som en integrert funksjon kan være angitt i de generelle vilkår: integralet av noen kraft f(x) = xr er xr+1⁄r+1, og det er andre integrerte funksjoner for eksponential-og logaritmefunksjoner, trigonometriske funksjoner, etc, slik at området under enhver kontinuerlig kurve kan fås mellom to grenser.,
Newton valgte ikke å publisere hans revolusjonerende matematikk gang, bekymret for å bli latterliggjort for sin ukonvensjonelle ideer, og tilfreds seg med sirkulerende hans tanker blant venner. Tross alt, han hadde mange andre interesser som for eksempel filosofi, alkymi og hans arbeid på Royal Mint. Imidlertid, i 1684, den tyske Leibniz publiserte sin egen uavhengige versjon av teorien, mens Newton publisert ingenting om emnet før 1693., Selv om the Royal Society, etter grundig overveielse, ga kreditt for det første funnet å Newton (og kreditt for det første publikasjonen til Leibniz), noe av en skandale oppsto da det ble offentliggjort at Royal Society påfølgende anklager om plagiat mot Leibniz faktisk var skrevet av ingen ringere Newton selv, forårsaker en pågående kontrovers som ødela karrieren til både menn.,
Generalisert Binomiske Teorem
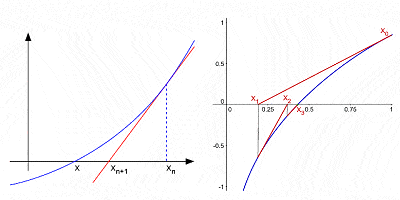
Newtons Metode for tilnærmet røtter i en kurve ved etterfølgende interations etter en innledende antar
til Tross for å være langt hans mest kjente bidrag til matematikk, matematisk analyse var på ingen måte Newtons bare bidrag.,raic utvidelse av krefter av en binomial (et algebraisk uttrykk med to vilkår, for eksempel a2 – b2); han laget vesentlig bidrag til teorien for endelige forskjeller (matematiske uttrykk på formen f(x + b) – f(x + a)); han var en av de første til å bruke brøk eksponenter og koordinere geometri for å utlede løsninger på Diophantine ligninger (algebraiske ligninger med heltall-bare variabler); han utviklet den såkalte «Newtons metode» for å finne suksessivt bedre tilnærming til nuller eller røtter av en funksjon; han var den første til å bruke uendelig strøm-serien med noen tillit, etc.,
I 1687, Newton ut sin «Principia» eller «De Matematiske Prinsippene for Naturlig Filosofi», generelt anerkjent som den største vitenskapelige bok som noensinne er skrevet. I det han presenterte sine teorier om bevegelse, gravitasjon og mekanikk, forklarte den eksentriske baner av kometer, tidevann og deres variasjoner, the precession av Jordens akse og bevegelse av Månen.,
Senere i livet skrev han en rekke religiøse traktater arbeider med bokstavelig tolkning av Bibelen, viet mye tid til alkymi, fungerte som Medlem av Parlamentet i noen år, og ble kanskje den mest kjente Master of the Royal Mint i 1699, en stilling han innehadde til sin død i 1727. I 1703 ble han gjort til President for the Royal Society, og i 1705, ble den første vitenskapsmann noensinne å bli slått til ridder. Kvikksølv forgiftning fra hans alkymistiske sysler kanskje forklart Newtons eksentrisitet senere i livet, og muligens også hans endelige død.,
| << Back to Pascal | Forward to Leibniz >> |
Leave a Reply