
統計は、アナリストが推論を行うために使用する統計検定の配置です与えられたデータから。 これらの試験できる意思決定の観測パターンからデータです。 広い範囲があります統計的検定の。 どの統計的検定を利用するかの選択は、データの構造、データの分布、および変数タイプに依存する。,T検定、Z検定、カイ二乗検定、anova検定、二項検定、一標本正中検定などの統計にはさまざまな種類の検定があります。
統計検定の選択-
データが正規分布している場合、パラメトリック検定が使用されます。パラメトリック統計検定では、母集団パラメーターとデータの由来となった分布について仮定します。 これらのタイプの検定には、データが正規分布からのものであると仮定するt検定、z検定、およびanova検定が含まれます。,
Z検定-z検定は、分散がわかっており、標本サイズが大きい場合に、二つの母平均が異なるかどうかを判断するために使用される統計的検定です。 Z検定では、母集団の平均が比較されます。使用されるパラメータは、母集団平均と母集団標準偏差です。 Z検定は、抽出された標本が同じ母集団に属するという仮説を検証するために使用されます。,
Ho:標本平均は母集団の平均と同じです(帰無仮説)
Ha:標本平均は母集団の平均と同じではありません(代替仮説)
z=(x-λ)/(λ/λ n)、
ここで、x=標本平均、u=母集団の平均、λ/λ n=母集団の標準偏差。
z値が臨界値より小さい場合は帰無仮説を受け入れ、そうでない場合は帰無仮説を拒否します。
T検定-t検定では、与えられた二つのサンプルの平均が比較されます。 T検定は、母パラメーター(平均および標準偏差)が不明な場合に使用されます。,
Paired T-Test-同じ母集団からの二つの変数間の差に対する検定(テスト前とテスト後のスコア)。 たとえば、プログラムの修了前後の研修生のトレーニングプログラムのパフォーマンススコア。
独立T検定-また、二つのサンプルt検定または学生のt検定と呼ばれる独立t検定は、二つの無関係なグループの平均間に統計的に有意な差があるかどうかを決定する統計的検定です。たとえば、人口の男の子と女の子を比較する。,
一つのサンプルt検定-単一のグループの平均が与えられた平均と比較されます。 たとえば、平均売上高が与えられている場合、売上高の増減を確認します。
t=(x1-x2)/(λ/λ n1+λ/λ n2)、
ここで、x1およびx2はそれぞれサンプル1およびサンプル2の平均である。
ANOVA検定-分散分析(ANOVA)は、複数のグループの平均が互いに有意に異なるかどうかを確認するために使用される統計的手法です。 ANOVAは、異なる標本の平均を比較することによって、一つ以上の因子の影響をチェックします。, ANOVAテストの代わりにtテストを使用すると、サンプル数が二つ以上であり、結果に誤差が生じるため、信頼できません。
ANOVAで検定される仮説は
Ho:サンプルのすべてのペアが同じである、すなわち、
Hoである。, anova検定では、F値を計算し、臨界値と比較します。
F=((SSE1—SSE2)/m)/SSE2/n-k、ここで
SSE=残差二乗和
m=制限の数
K=独立変数の数
ノンパラメトリック統計test-ノンパラメトリック検定は、データが正規分布していない場合に使用されます。 非パラメトリック検定にはカイ二乗検定があります。
カイ二乗検定(λ2検定)-カイ二乗検定は、二つのカテゴリ変数を比較するために使用されます。, カイ二乗統計値を計算し、それをカイ二乗分布からの臨界値と比較することで、観測された頻度が期待される頻度と有意に異なるかどうかを評価
カイ二乗について検定されている仮説は-である
Ho:変数xと変数yは独立している
Ha:変数xと変数yは独立していない。,
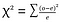
where o=observed , e=expected.
Leave a Reply