ISAAC NEWTON:Math&Calculus

Sir Isaac Newton(1643-1727)

17世紀のイギリスの酔わせるような雰囲気の中で、大英帝国の本格的な拡大に伴い、オックスフォードやケンブリッジのような壮大な古い大学は多くの偉大な科学者や数学者を輩出していた。 でも最大のしめるようになったたなサー Isaac Newton.,

物理学者、数学者、天文学者、自然哲学者、錬金術師、神学者、ニュートンは、人類史上最も影響力のある男性の一人であると多くの人が考えています。 彼の1687年の出版物、”Philosophiae Naturalis Principia Mathematica”（通常は単に”Principia”と呼ばれる）は、科学史の中で最も影響力のある本の一つであると考えられており、次の三世紀にわたって物,

重力とリンゴの木の物語と今日の一般市民の心の中で主に同義が、ニュートンは（アルキメデスやガウスのようなすべての時間の偉人と同等に）どこ

二つの奇跡的な年にわたって、1665年6月の大ペストの時に、若いニュートンは、光の新しい理論を開発し、発見し、重力を定量化し、数学への革命的な新しいアプローチを開拓しました：無限小微積分。, 彼の微積分学の理論は、彼の仲間のイギリス人ジョン-ウォリスとアイザック-バローによる以前の仕事だけでなく、ルネ-デカルト、ピエール-ド-フェルマー、ボナヴェンチュラ-カヴァリエリ、ヨハン-ファン-ウェーヴェレン-フッデ、ジル-ペルンヌ-ド-ロベルヴァルのような大陸数学者の仕事に基づいて構築された。 ギリシャ人の静的幾何学とは異なり、微積分学は、数学者や技術者が惑星の軌道、流体の動きなど、私たちの周りの変化する世界の動きと動的変化を理,

曲線の平均勾配

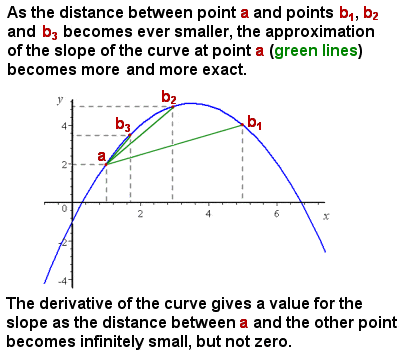
微分（微分）は、区間がゼロに近づくにつれて曲線の傾きを近似します

ニュートンが直面していた最初の問題は、曲線の平均勾配（例えば、時間距離グラフ上のオブジェクトの速度の増加）を表して計算するのは簡単でしたが、曲線の傾きは次のようになっていました。絶えず変化し、曲線上のいずれかの個々の点で正確な傾きを与える方法はありませんでした。, その点における曲線に対する接線の傾きを効果的に表します。

直感的には、特定の点における傾きは、曲線のこれまでに小さいセグメントの平均傾き（”ライズオーバーラン”）を取ることによって近似することができる。 考慮される曲線のセグメントがサイズがゼロに近づくにつれて（すなわち、xの無限小変化）、勾配の計算はある点で正確な勾配に近づく（右の画像を参照）。,

あまりにも複雑な詳細に入ることなく、ニュートン（および彼の現代のゴットフリート-ライプニッツ）は、関数f（x）の任意の点で傾きを与える微分関数f’（x） 曲線や関数の傾きや導関数を計算するこのプロセスは、微分計算や微分と呼ばれています（または、ニュートンの用語では、”フラクシオンの方法”–彼は曲線上の特定の点での瞬間的な変化率を”フラクシオン”、xとyの変化する値を”フルエント”と呼んでいます）。, 例えば、f(x)=4x型の直線の導関数はちょうど4であり、二乗函数f(x)=x2の導関数は2xであり、三次函数f(x)=x3の導関数は3×2である。 一般化すると、任意のべき関数f(x)=xrの導関数はrxr-1である。 指数関数関数や対数関数、sin(x)、cos(x)などの三角関数に対して、一定の規則に従って他の微分関数を記述することができるので、微分関数は不連続のない任意の曲線に対して記述することができる。, 例えば、曲線f(x)=x4-5×3+sin(x2)の導関数は、f'(x)=4×3–15×2+2xcos(x2)となる。

特定の曲線の微分関数を確立したら、xの値を挿入するだけで、その曲線上の特定の点での傾きを計算するのは簡単です。,

Fluentsの方法

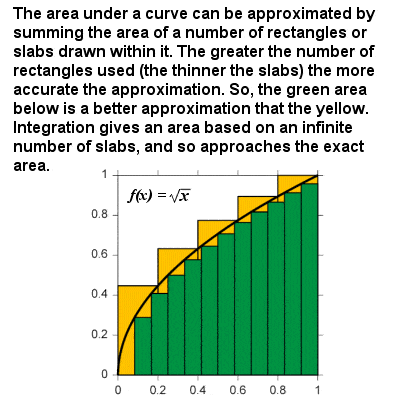
積分は、サンプルのサイズがゼロに近づくにつれて曲線下の面積を近似します

微分の”反対”は積分または積分計算（またはニュートンの用語では”fluentsの方法”）であり、微分と積分は微積分の二つの主要な操作である。, ニュートンの微積分の基本定理は、微分と積分は逆演算であると述べているので、関数が最初に積分されてから微分される（またはその逆）場合、元の関数が取り出される。

曲線の積分は、曲線で囲まれた面積と定義された二つの境界の間のx軸を計算するための式と考えることができます。 たとえば、時間に対する速度のグラフでは、”曲線下”の領域は移動距離を表します。, 本質的に、積分は、曲線領域の面積を無限に薄い垂直スラブまたは柱に分割することによって近似する制限手順に基づいている。 微分と同じように、積分関数は一般に言うことができる：任意のべき乗f(x)=xrの積分はxr+1≤r+1であり、指数関数関数と対数関数、三角関数などに対する他の積分関数があり、任意の連続曲線の下の面積は任意の二つの極限の間で得ることができる。,

ニュートンは、彼の革新的な数学をすぐに公開しないことを選び、彼の型破りなアイデアのために嘲笑されることを心配し、友人の間で彼の考えを循環させることで自分自身を満足させた。 結局のところ、彼は哲学、錬金術、王立造幣局での彼の仕事など、他の多くの興味を持っていました。 しかし、1684年にドイツのライプニッツはこの理論の独自の独立版を出版したが、ニュートンは1693年までこの問題については何も出版しなかった。, 王立協会は、十分な審議の後、ニュートンに最初の発見のためのクレジット（およびライプニッツへの最初の出版物のためのクレジット）を与えたが、それはライプニッツに対する盗作の王立協会のその後の告発が実際に他のニュートン自身によって書かれていないことを公表したときにスキャンダルのようなものが起こり、両方の男性のキャリアを損なう継続的な論争を引き起こした。,

一般化された二項定理

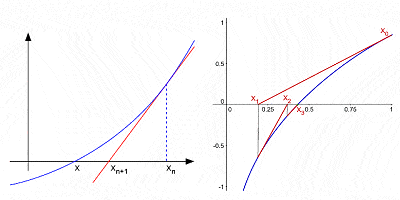
最初の推測の後に連続した相互作用によって曲線の根を近似するためのニュートンの方法

数学への彼の最もよく知られている貢献であるにもかかわらず、微積分は決してニュートンの唯一の貢献ではなかった。,二項のべき乗のraic展開（a2–b2などの二つの項を持つ代数式）;彼は有限差分の理論（f（x+b）–f（x+a）の形式の数式）にかなりの貢献をした;彼はディオファントス方程式（整数のみの変数を持つ代数方程式）の解を導くために分数指数と座標幾何学を使用した最初の一人であった;彼は関数のゼロまたは根に連続的により良い近似を見つけるためのいわゆる”ニュートン法”を開発した。自信を持ってパワーシリーズ;など。,

1687年、ニュートンは”Principia”または”The Mathematical Principles of Natural Philosophy”を出版し、これまでに書かれた最大の科学書として一般的に認められています。 その中で、彼は運動、重力、力学の理論を提示し、彗星の偏心軌道、潮汐とその変動、地球の軸の歳差運動、月の動きを説明しました。,

その後、彼は聖書の文字通りの解釈を扱ういくつかの宗教的な道を書き、錬金術に多くの時間を費やし、何年かの間議会のメンバーとして行動し、1699年に王立造幣局の最もよく知られたマスターとなり、1727年に死ぬまで務めた。 1703年に王立協会の会長となり、1705年にナイトに叙された最初の科学者となった。 彼の錬金術の追求からの水銀中毒は、おそらく後の人生でニュートンの偏心を説明し、おそらく彼の最終的な死も説明しました。,