
Sir Isaac Newton (1643-1727)
Az a mámorító hangulat, a 17. Században Anglia, a terjeszkedés, a Brit birodalom javában, a régi nagy egyetemek, mint Oxford Cambridge-ben volt, azóta számos nagyszerű tudósok, matematikusok. De a legnagyobb közülük kétségtelenül Sir Isaac Newton volt.,
fizikus, matematikus, csillagász, természettudós, alkimista és teológus, Newtont sokan az emberi történelem egyik legbefolyásosabb emberének tartják. 1687-es kiadványa, A ” Philosophiae Naturalis Principia Mathematica “(általában” Principia”) a tudomány történetének egyik legbefolyásosabb könyve, amely a következő három évszázadban uralta a fizikai univerzum tudományos nézetét.,
bár a nagyközönség elméjében ma a gravitáció és az almafa története nagyrészt megegyezik, Newton mindenütt óriás marad a matematikusok elméjében (hasonlóan a Minden idők nagyjaihoz, mint Archimedes és Gauss), és nagyban befolyásolta a matematikai fejlődés későbbi útját.
két csodálatos év alatt, az 1665-6-os nagy pestis idején, a fiatal Newton kifejlesztette a fény új elméletét, felfedezte és számszerűsítette a gravitációt, és úttörő szerepet játszott a matematika forradalmi új megközelítésében: az infinitezimális kalkulusban., A kalkulus elmélete John Wallis és Isaac Barrow angol kollégái korábbi munkáira épült, valamint olyan kontinentális matematikusok munkáira, mint René Descartes, Pierre de Fermat, Bonaventura Cavalieri, Johann van Waveren Hudde és Gilles Personne de Roberval. A görögök statikus geometriájával ellentétben a kalkulus lehetővé tette a matematikusok és mérnökök számára, hogy megértsék a körülöttünk lévő változó világban a mozgást és a dinamikus változást, például a bolygók pályáját, a folyadékok mozgását stb.,
Az Átlagos Lejtése egy Görbe
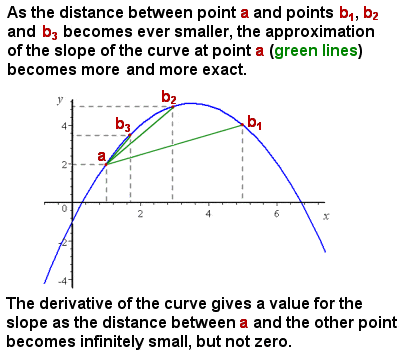
Differenciálás (derivatív) megközelíti a lejtőn egy görbe, mint az intervallum módszerek nulla
A kezdeti probléma Newton volt, szembenézve az volt, hogy bár könnyű volt elég, hogy képviselje, s számítsuk ki az átlagos lejtése egy görbe (például a sebesség növelésével egy tárgy, egy idő-távolság grafikon), a lejtőn egy görbe folyamatosan változó, nincs módszer, hogy a pontos lejtőn az egyén pont a görbe, azaz, hatékonyan a lejtőn egy érintő vonal a görbe ezen a ponton.
intuitív módon a lejtés egy adott ponton közelíthető a görbe egyre kisebb szegmenseinek átlagos lejtésével (“emelkedés futás közben”). Mivel a figyelembe vett görbe szegmense mérete megközelíti a nullát (azaz az X végtelen változását), akkor a lejtő kiszámítása egyre közelebb kerül a pontos lejtőhöz egy ponton (lásd a jobb oldali képet).,
anélkül, hogy túl bonyolult részletekbe ment volna, Newton (és kortárs Gottfried Leibniz önállóan) kiszámított egy f ‘(x) függvény deriváltfüggvényt, amely az f(x) függvény bármely pontján megadja a meredekséget. Ez a folyamat kiszámítása a lejtőn, vagy származéka egy görbe vagy függvény differenciálszámítás, vagy differenciálás (vagy Newton terminológia, a “módszer fluxió” – hívta a pillanatnyi változás mértéke egy bizonyos pont, görbe a “fluxion”, majd a változó értéke x, az y pedig a “fluents”)., Például az F(x) = 4x típusú egyenes vonal származéka csak 4; az f(x) = x2 négyzetfüggvény származéka 2x; az F(x) = x3 köbfüggvény származéka 3×2 stb. Általánosítva, bármely F(x) = xr teljesítményfüggvény származéka rxr-1. Egyéb származékos funkciók elmondható, bizonyos szabályok szerint, az exponenciális, illetve logaritmikus függvények, trigonometrikus függvények például a sin(x), cos(x), stb, szóval, hogy egy származtatott funkció elmondható, bármilyen görbe nélkül töréseket., Például az F(x) = x4 – 5×3 + sin(x2) görbe származéka f ‘(x) = 4×3 – 15×2 + 2xcos(x2).
miután meghatározta egy adott görbe deriváltfüggvényét, akkor könnyű kérdés a lejtő meszesedése a görbe bármely pontján, csak egy x érték beillesztésével. időtávolságú grafikon esetén például ez a lejtő az objektum sebességét képviseli egy adott ponton.,
A Fluentusok módszere
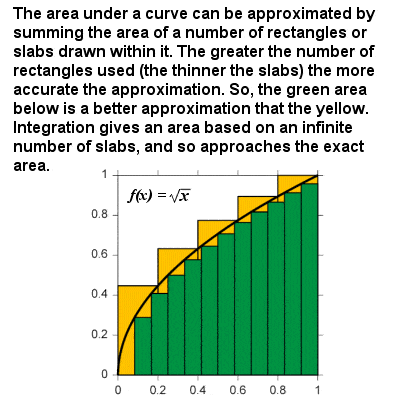
integráció közelíti a görbe alatti területet, mivel a minták mérete megközelíti a nullát
a differenciálás “ellentéte” az integráció vagy az integrált kalkulus (vagy Newton terminológiájában a “fluentusok módszere”), és a differenciálás és az integráció együtt a kalkulus két fő művelete., Newton kalkulus alaptétele szerint a differenciálás és az integráció inverz műveletek, így ha EGY függvényt először integrálnak, majd differenciálnak (vagy fordítva), akkor az eredeti függvény visszakereshető.
egy görbe integrálja a görbe által határolt terület és a két meghatározott határ közötti x tengely kiszámításának képleteként értelmezhető. Például, egy grafikonon a sebesség az idővel, a terület “a görbe alatt” jelentené a megtett távolságot., Lényegében az integráció egy korlátozó eljáráson alapul, amely megközelíti a görbe vonalú régió területét azáltal, hogy végtelenül vékony függőleges lemezekre vagy oszlopokra bontja. Ugyanúgy, mint a differenciálás, szerves funkció elmondható általánosságban: a szerves sem hatalom, f(x) = xr xr+1⁄r+1, egyéb szerves funkciók, exponenciális, illetve logaritmikus függvények, trigonometrikus függvények, stb, szóval, hogy a terület alatt folyamatos görbe lehet beszerezni között két határérték.,
Newton úgy döntött, hogy nem adja ki azonnal forradalmi matematikáját, aggódik amiatt, hogy nevetségessé válik szokatlan ötletei miatt, és megelégedett azzal, hogy gondolatait a barátok között terjeszti. Végül is sok más érdeklődése volt, mint a filozófia, az alkímia és a királyi pénzverdében végzett munkája. 1684-ben azonban a német Leibniz kiadta az elmélet saját független változatát, míg Newton 1693-ig semmit sem tett közzé a témáról., Bár a Royal Society, miután kellő megfontolás, adta hitelt az első felfedezés Newton (és hitelt az első kiadvány Leibniz), valami botrány merült fel, amikor nyilvánosságra hozták, hogy a Royal Society későbbi vádja plágium ellen Leibniz valójában szerzője más Newton magát, ami egy folyamatos vita, amely tönkretette a karrier mindkét férfi.,
Általánosított Binomiális Tétel
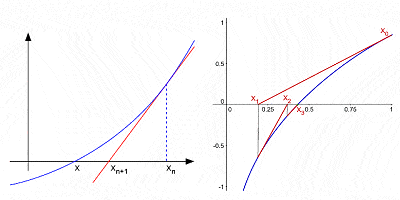
Newton Módszer egyébként a gyökerek egy görbe egymást követő interations a kezdeti hiszem,
annak Ellenére, hogy messze a legjobb ismert hozzájárulása a matematika, a matematika volt, nem azt jelenti, hogy Newton csak hozzájárulás.,raic bővítése hatáskörét egy binomiális (algebrai kifejezés két kifejezések, mint például a2 – b2); tett jelentős hozzájárulás az elmélet véges különbségek (matematikai kifejezések a forma f(x + b) – f(x + a)); ő volt az egyik első, hogy frakcionált is, illetve koordináta-geometria hogy ebből megoldások Diophantine egyenletek (algebrai egyenletek az egész-csak változók); ő fejlesztette ki az úgynevezett “Newton-módszer” a megállapítás egymás jobb közelítések a nulla vagy gyökerei a funkció; ő volt az első, hogy végtelen hatalom sorozat semmilyen bizalom; stb.,
1687-ben Newton kiadta “Principia” vagy “a természetes filozófia matematikai elveit”, amelyet általánosan elismertek a valaha írt legnagyobb tudományos könyvnek. Ebben bemutatta a mozgás, a gravitáció és a mechanika elméleteit, elmagyarázta az üstökösök excentrikus pályáit, az árapályokat és azok variációit, a Föld tengelyének precesszióját és a Hold mozgását.,
Az élet későbbi szakaszában számos vallási traktust írt, amelyek a Biblia szó szerinti értelmezésével foglalkoztak, sok időt szenteltek az alkímiának, néhány évig parlamenti képviselő volt, és 1699-ben a Királyi Pénzverde talán legismertebb mestere lett, ezt a pozíciót 1727-es haláláig töltötte be. 1703-ban a Királyi Társaság elnöke lett, 1705-ben pedig ő lett az első tudós, akit lovaggá ütöttek. A higanymérgezés az alkímiai törekvéseiből talán Newton excentricitását magyarázta a későbbi életben, és valószínűleg az esetleges halálát is.,
| << Back to Pascal | Forward to Leibniz >> |
Leave a Reply