
Sir Isaac Newton (1643-1727)
dans l’atmosphère capiteuse de L’Angleterre du 17ème siècle, avec l’expansion de l’empire britannique en plein essor, grandes vieilles universités comme Oxford et Cambridge ont produit de nombreux grands scientifiques et mathématiciens. Mais le plus grand de tous était sans aucun doute Sir Isaac Newton.,
physicien, mathématicien, astronome, philosophe naturel, alchimiste et théologien, Newton est considéré par beaucoup comme l’un des hommes les plus influents de l’histoire humaine. Sa publication de 1687, le » Philosophiae Naturalis Principia Mathematica « (généralement appelé simplement le” Principia »), est considéré comme l’un des livres les plus influents dans l’histoire de la science, et il a dominé la vision scientifique de l’univers physique pour les trois siècles suivants.,
bien que largement synonyme dans l’esprit du grand public aujourd’hui avec la gravité et l’histoire du pommier, Newton reste un géant dans l’esprit des mathématiciens du monde entier (à égalité avec les grands de tous les temps comme Archimède et Gauss), et il a grandement influencé le chemin ultérieur du développement mathématique.
pendant deux années miraculeuses, à l’époque de la Grande Peste de 1665-6, Le Jeune Newton développa une nouvelle théorie de la lumière, découvrit et quantifia la gravitation, et fut le pionnier d’une nouvelle approche révolutionnaire des mathématiques: le calcul infinitésimal., Sa théorie du calcul s’appuie sur les travaux antérieurs de ses collègues anglais John Wallis et Isaac Barrow, ainsi que sur les travaux de mathématiciens continentaux tels que René Descartes, Pierre de Fermat, Bonaventura Cavalieri, Johann van Waveren Hudde et Gilles personne de Roberval. Contrairement à la géométrie statique des Grecs, le calcul a permis aux mathématiciens et aux ingénieurs de donner un sens au mouvement et au changement dynamique du monde changeant qui nous entoure, tels que les orbites des planètes, le mouvement des fluides, etc.,
la pente moyenne d’une courbe
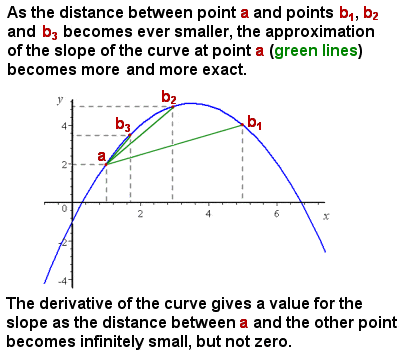
La Différenciation (dérivée) se rapproche de la pente d’une courbe lorsque l’intervalle approche de zéro
le problème initial auquel Newton était confronté était que, bien qu’il soit assez facile de représenter et de calculer la pente moyenne la pente d’une courbe variait constamment, et il n’y avait pas de méthode pour donner la pente exacte à un point individuel de la courbe, c’est-à-dire, effectivement la pente d’une tangente à la courbe en ce point.
intuitivement, la pente en un point particulier peut être approximée en prenant la pente moyenne (« rise over run”) de segments de plus en plus petits de la courbe. Comme le segment de la courbe considérée approche de zéro en taille (c’est-à-dire un changement infinitésimal en x), alors le calcul de la pente se rapproche de plus en plus de la pente exacte en un point (voir image à droite).,
Sans entrer dans trop de détails compliqués, Newton (et son contemporain Gottfried Leibniz indépendamment) ont calculé une fonction dérivée f ‘(x) qui donne la pente en tout point d’une fonction f(x). Ce processus de calcul de la pente ou de la dérivée d’une courbe ou d’une fonction est appelé calcul différentiel ou différenciation (ou, dans la terminologie de Newton, la « méthode des fluxions” – il a appelé le taux de changement instantané à un point particulier d’une courbe la « fluxion”, et les valeurs changeantes de x et y les « fluents”)., Par exemple, la dérivée d’une droite de type f(x) = 4X est juste 4; la dérivée d’une fonction carrée f(x) = x2 est 2x; la dérivée de la fonction cubique f(x) = x3 est 3×2, etc. En généralisant, la dérivée de toute fonction de puissance f(x) = xr est rxr-1. D’autres fonctions dérivées peuvent être énoncées, selon certaines règles, pour les fonctions exponentielles et logarithmiques, les fonctions trigonométriques telles que sin(x), cos(x), etc., de sorte qu’une fonction dérivée peut être énoncée pour n’importe quelle courbe sans discontinuités., Par exemple, la dérivée de la courbe de f(x) = x4 – 5×3 + sin(x2) serait f ’(x) = 4×3 – 15×2 + 2xcos(x2).
Après avoir établi la fonction dérivée pour une courbe particulière, il est alors facile de calculer la pente en un point particulier de cette courbe, simplement en insérant une valeur pour X. Dans le cas d’un graphe temps-distance, par exemple, cette pente représente la vitesse de l’objet en un point particulier. ,
méthode des Fluents
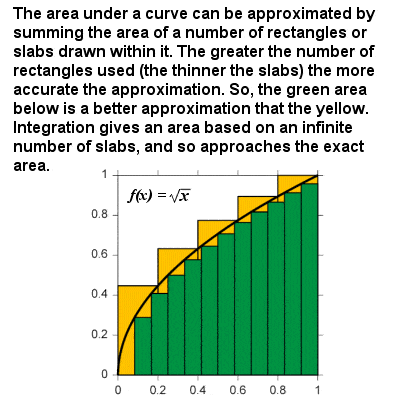
L’intégration se rapproche de l’aire sous une courbe lorsque la taille des échantillons approche de zéro
le « contraire” de la différenciation est l’intégration ou le calcul intégral (ou, dans la terminologie de Newton, la « méthode des fluents”), et ensemble la différenciation et l’intégration sont les deux principales opérations du calcul., Le théorème fondamental de calcul de Newton stipule que la différenciation et l’intégration sont des opérations inverses, de sorte que, si une fonction est d’abord intégrée puis différenciée (ou vice versa), la fonction d’origine est récupérée.
L’intégrale d’une courbe peut être considéré comme la formule pour calculer l’aire délimitée par la courbe et l’axe des x entre deux limites définies. Par exemple, sur un graphique de vitesse contre temps, l’aire « sous la courbe” représenterait la distance parcourue., Essentiellement, l’intégration est basée sur une procédure de limitation qui se rapproche de l’aire d’une région curviligne en la décomposant en dalles ou colonnes verticales infinitésimalement minces. De la même manière que pour la différenciation, une fonction intégrale peut être énoncés en termes généraux: l’intégrale de f(x) = xr, xr+1⁄r+1, et il ya d’autres fonctions intégrales pour exponentielles et logarithmiques fonctions, fonctions trigonométriques, etc, de sorte que la superficie de toute courbe peut être obtenue entre deux limites.,
Newton choisit de ne pas publier immédiatement ses mathématiques révolutionnaires, craignant d’être ridiculisé pour ses idées non conventionnelles, et se contentant de faire circuler ses pensées entre amis. Après tout, il avait beaucoup d’autres intérêts tels que la philosophie, l’alchimie et son travail à la Monnaie royale. Cependant, en 1684, l’Allemand Leibniz a publié sa propre version indépendante de la théorie, tandis que Newton n’a rien publié sur le sujet jusqu’en 1693., Bien que la Royal Society, après délibération, a donné le crédit pour la première découverte à Newton (et le crédit pour la première publication à Leibniz), quelque chose d’un scandale a surgi quand il a été rendu public que l’accusation ultérieure de plagiat de la Royal Society contre Leibniz était en fait écrit par aucun autre Newton lui-même, provoquant une controverse,
théorème Binomial généralisé
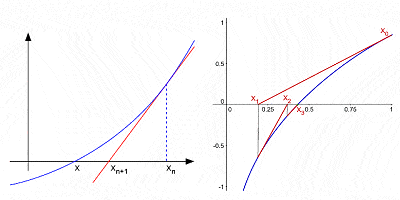
méthode de Newton pour approximer les racines d’une courbe par des interations successives après une supposition initiale
bien qu’étant de loin sa contribution la plus connue aux mathématiques, le calcul n’était en aucun cas la seule contribution de Newton.,Raic expansion of powers of a binomial (an algebraic expression with two terms, such as a2 – b2); il a apporté des contributions substantielles à la théorie des différences finies (expressions mathématiques de la forme f(x + b) – f(x + a)); il a été l’un des premiers à utiliser les exposants fractionnaires et la géométrie des coordonnées pour dériver des solutions aux équations diophantiennes (équations algébriques avec des variables entières seulement); il a développé la soi-disant « méthode de Newton” pour trouver successivement de meilleures approximations aux zéros ou aux racines d’une fonction; il a été le premier pour employer la série infinie de puissance avec n’importe quelle confiance; etc.,
en 1687, Newton a publié ses « Principia” ou « les principes mathématiques de la philosophie naturelle”, généralement reconnu comme le plus grand livre scientifique jamais écrit. Il y présentait ses théories du mouvement, de la gravité et de la mécanique, expliquait les orbites excentriques des comètes, les marées et leurs variations, la précession de l’axe de la Terre et le mouvement de la Lune.,
plus tard dans sa vie, il écrivit un certain nombre de tracts religieux traitant de l’interprétation littérale de la Bible, consacra beaucoup de temps à l’alchimie, fut député pendant quelques années et devint peut-être le maître le plus connu de la Monnaie royale en 1699, poste qu’il occupa jusqu’à sa mort en 1727. En 1703, il est nommé président de la Royal Society et, en 1705, devient le premier scientifique à être fait chevalier. L’empoisonnement au mercure de ses activités alchimiques a peut-être expliqué L’excentricité de Newton plus tard dans la vie, et peut-être aussi sa mort éventuelle.,
| << Back to Pascal | Forward to Leibniz >> |
Leave a Reply