
Las estadísticas son el arreglo de las pruebas estadísticas que se emplean para hacer inferencia a partir de los datos dados. Estas pruebas nos permiten tomar decisiones sobre la base del patrón observado a partir de los datos. Existe una amplia gama de pruebas estadísticas. La elección de qué prueba estadística utilizar se basa en la estructura de los datos, la distribución de los datos y el tipo de variable.,Hay muchos tipos diferentes de pruebas en estadísticas como la prueba t,la prueba Z,la prueba chi-cuadrado, la prueba anova ,la prueba binomial, la prueba Mediana de una muestra, etc.
elegir una prueba estadística –
Las pruebas paramétricas se utilizan si los datos se distribuyen normalmente .Una prueba estadística paramétrica hace una suposición sobre los parámetros poblacionales y las distribuciones de las que provienen los datos. Estos tipos de pruebas incluyen pruebas t, pruebas z y pruebas anova, que asumen que los datos son de distribución normal.,
prueba Z-una prueba z es una prueba estadística utilizada para determinar si dos medias de población son diferentes cuando se conocen las varianzas y el tamaño de la muestra es grande. En la prueba z se compara la media de la población.Los parámetros utilizados son la media poblacional y la desviación estándar poblacional. Z-test se utiliza para validar una hipótesis de que la muestra dibujada pertenece a la misma población.,
Ho: la media muestral es la misma que la media poblacional(hipótesis nula)
Ha: la media muestral no es la misma que la media poblacional (hipótesis alternativa)
z = (x — μ) / (σ / √n),
where , x=media muestral, u=media poblacional, σ / √n = desviación estándar poblacional.
si el valor z es menor que el valor crítico aceptar hipótesis nula de lo contrario rechazar hipótesis nula.
t-test-en t-test se compara la media de las dos muestras dadas. Se utiliza una prueba t cuando no se conocen los parámetros poblacionales (media y desviación estándar).,
Test T Pareado-prueba de la diferencia entre dos variables de la misma población( puntuación pre y post test). Por ejemplo-en un programa de formación puntuación de rendimiento del aprendiz antes y después de la finalización del programa.
Prueba T independiente – la prueba t independiente que también se llama prueba t de dos muestras o prueba t de student, es una prueba estadística que determina si hay una diferencia estadísticamente significativa entre las medias en dos grupos no relacionados.Por ejemplo, comparar niños y niñas en una población.,
prueba t de una muestra-la media de un solo grupo se compara con una media dada. Por ejemplo-para comprobar el aumento y la disminución de las ventas si se da el promedio de ventas.
t = (x1 — x2) / (σ / √n1 + σ / √n2),
donde x1 y x2 son la media de la muestra 1 y la muestra 2, respectivamente.
Prueba de Anova-análisis de varianza (ANOVA) es una técnica estadística que se utiliza para comprobar si las medias de dos o más grupos son significativamente diferentes entre sí. ANOVA comprueba el impacto de uno o más factores comparando los medios de diferentes muestras., Si usamos una prueba t en lugar de la prueba ANOVA, no será confiable ya que el número de muestras es más de dos y dará un error en el resultado.
la hipótesis que se está probando en ANOVA es
Ho: todos los pares de muestras son iguales i. e., todas las medias de la muestra son iguales
Ha: Al menos un par de muestras es significativamente diferente
en la prueba anova calculamos el valor F y lo comparamos con el valor crítico
F= ((SSE1 — SSE2)/m)/ SSE2/n-k, donde
SSE = suma residual de cuadrados
m = Número de restricciones
k = número de variables independientes
estadística no paramétrica prueba – las pruebas no paramétricas se utilizan cuando los datos no se distribuyen normalmente. Las pruebas no paramétricas incluyen la prueba de chi-cuadrado.
Prueba de Chi-cuadrado (prueba χ2)-la prueba de chi-cuadrado se utiliza para comparar dos variables categóricas., Calcular el valor estadístico Chi-Cuadrado y compararlo con un valor crítico de la distribución Chi-cuadrado permite evaluar si la frecuencia observada es significativamente diferente de la frecuencia esperada.
la hipótesis que se está probando para chi-cuadrado es-
Ho: la Variable x y la Variable y son independientes
Ha: la Variable x y la Variable y no son independientes.,
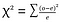
where o=observed , e=expected.
Leave a Reply