
Sir Isaac Newton (1643-1727)
I den berusende atmosfære af 17 Århundrede England, med ekspansionen af det Britiske imperium i fuld gang, grand old universiteter som Oxford og Cambridge, var at producere mange store videnskabsmænd og matematikere. Men den største af dem alle var utvivlsomt Sir Isaac ne .ton.,
Fysiker, matematiker, astronom, naturlige filosof, alkymist og teolog, Newton anses af mange for at være en af de mest indflydelsesrige mænd i menneskets historie. Hans 1687 publikation, “Philosophiae Naturalis Principia Mathematica” (normalt kaldes simpelthen “Principia”), anses for at være blandt de mest indflydelsesrige bøger i videnskabens historie, og det dominerede den videnskabelige opfattelse af det fysiske univers for de næste tre århundreder.,
Selv om stort set synonymt i hovedet på den brede offentlighed i dag med tyngdekraften og historien om æbletræet, Newton forbliver en gigant i hovedet af matematikere overalt (på niveau med de all-time greats som Archimedes og Gauss), og han har i høj grad påvirket den efterfølgende sti af matematiske udvikling.
i Løbet af to mirakuløse år, i den tid af den Store Pest i 1665-6, den unge Newton har udviklet en ny teori for lys, opdaget og kvantificeres på gravitation, og det banebrydende for en revolutionerende ny tilgang til matematik: infinitesimale calculus., Hans teori om calculus bygget på tidligere arbejde af hans kolleger Englænderne John Wallis og Isaac Barrow, samt om arbejdet af en sådan Kontinental matematikere som René Descartes, Pierre de Fermat, Bonaventura Cavalieri, Johann van Waveren Hudde og Gilles Personne de Roberval. I modsætning til grækernes statiske geometri tillod calculus matematikere og ingeniører at give mening om bevægelsen og den dynamiske ændring i den skiftende verden omkring os, såsom planeternes baner, bevægelse af væsker osv.,
Den Gennemsnitlige Hældning af en Kurve
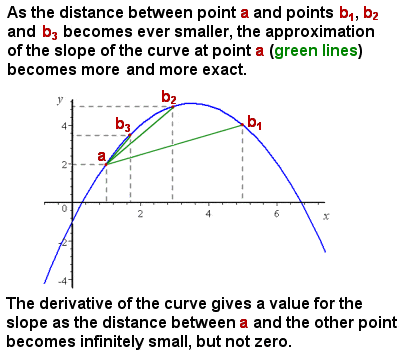
Differentiering (afledte) ligner hældningen af en kurve, som interval nærmer sig nul
Det oprindelige problem, Newton var at konfrontere var, at selvom det var let nok til at repræsentere og beregne den gennemsnitlige hældning af en kurve (for eksempel, den stigende hastighed af et objekt på et tidspunkt-afstand graf), hældning af en kurve, der var konstant varierende, og der var ingen metode til at give den nøjagtige hældning på én enkelte punkt på kurven, dvs, effektivt hældningen af en tangent linje til kurven på dette punkt.
intuitivt kan hældningen på et bestemt punkt tilnærmes ved at tage den gennemsnitlige hældning (“stigning over løb”) af stadig mindre segmenter af kurven. Da segmentet af kurven, der overvejes, nærmer sig nul i størrelse (dvs.en uendelig lille ændring i.), nærmer beregningen af hældningen tættere og tættere på den nøjagtige hældning på et punkt (se billedet til højre).,
uden at gå ind i for meget komplicerede detaljer, ne .ton (og hans moderne Gottfried Leibni.uafhængigt) beregnet en derivatfunktion F ‘((), som giver hældningen på ethvert punkt af en funktion f (.). Denne proces med at beregne hældningen eller afledt af en kurve eller en funktion, der kaldes differential regning eller differentiering (eller, i Newton ‘ s terminologi, “method of fluxions” – han kaldte den øjeblikkelige procentvise ændring på et bestemt punkt på en kurve på “fluxion”, og de skiftende værdier af x og y “fluents”)., For eksempel er derivatet af en lige linje af typen f ( = ) = 4.kun 4; derivatet af en kvadratisk funktion f (.) = .2 er 2.; derivatet af kubisk funktion f (.) = 43 er 3 .2 osv. Generalisering er derivatet af enhver effektfunktion f ( = ) = =r r .r-1. Andre afledte funktioner kan angives i henhold til visse regler for eksponentielle og logaritmiske funktioner, trigonometriske funktioner såsom sin (.), cos (.) osv., så en afledt funktion kan angives for enhver kurve uden diskontinuiteter., For eksempel ville derivatet af kurven f (.) =44 – 5 .3 + sin(sin2) være f ‘(.) = 4 .3 – 15 .2 + 2 .cos(.2).
efter at Have konstateret den afledte funktion til en bestemt kurve, så er det en let sag at calcuate hældningen på et bestemt punkt på kurven, blot ved at indsætte en værdi for x. I tilfælde af en tid-afstand graf, for eksempel, denne skråning repræsenterer den hastighed et objekt på et bestemt punkt.,
Metode til Fluents
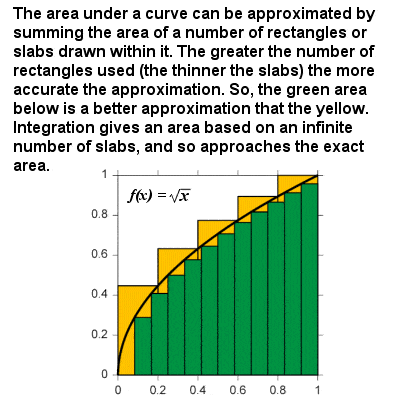
Integration tilnærmer arealet under en kurve, som størrelsen af de prøver, der nærmer sig nul
Det “modsatte” af differentiering og integration eller integralregning (eller, i Newton ‘ s terminologi, “metode til fluents”), og sammen differentiering og integration er de to vigtigste aktiviteter i calculus., Ne .tons grundlæggende sætning af beregning siger, at differentiering og integration er inverse operationer, så hvis en funktion først integreres og derefter differentieres (eller omvendt), hentes den oprindelige funktion.
integralet af en kurve kan betragtes som formlen til beregning af arealet afgrænset af kurven og axis-aksen mellem to definerede grænser. For eksempel, på en graf over hastighed mod tiden, ville området “under kurven” repræsentere den tilbagelagte afstand., Hovedsagelig, integration er baseret på en begrænsende procedure, som tilnærmer arealet af en krum region ved at bryde det ind infinitesimalt tynde lodrette plader eller søjler. På samme måde som for differentiering kan en integreret funktion angives generelt: integralet af enhver effekt f (.) = =r er .r+1⁄r+1, og der er andre integrerede funktioner til eksponentielle og logaritmiske funktioner, trigonometriske funktioner osv., så området under enhver kontinuerlig kurve kan opnås mellem to grænser.,
ne .ton valgte ikke at offentliggøre sin revolutionerende matematik med det samme, bekymret for at blive latterliggjort for hans ukonventionelle ideer, og tilfreds selv med at cirkulere sine tanker blandt venner. Han havde trods alt mange andre interesser som filosofi, alkymi og hans arbejde på Royal Mint. Men i 1684, den tyske Leibni.offentliggjort sin egen uafhængige version af teorien, mens ne .ton offentliggjort noget om emnet indtil 1693., Selv om Royal Society, efter nøje overvejelser, gav kredit for det første opdagelsen af, at Newton (og æren for den første offentliggørelse til Leibniz), noget af en skandale, som opstod, da det blev offentliggjort, at Royal Society ‘ s efterfølgende anklage om plagiat mod Leibniz var faktisk forfattet af ingen andre Newton selv, der forårsager en igangværende kontrovers, som rystede karriere både for mænd.,
Generaliseret Binomiale Sætning
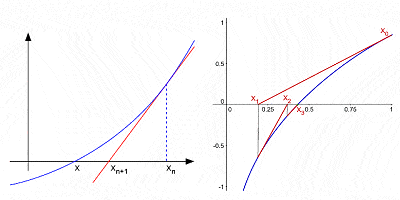
Newton ‘s Metode til at tilnærme rødderne af en kurve af efterfølgende interations efter et indledende gæt
på Trods af at være langt hans bedst kendte bidrag til matematik, regning var på ingen måde Newton’ s eneste bidrag.,raic udvidelse af beføjelser til en binomial (et algebraisk udtryk med to begreber, såsom a2 – b2); han har gjort betydelige bidrag til teorien om begrænsede forskelle (matematiske udtryk af formen f(x + b) – f(x + a)); han var en af de første til at bruge relativ eksponenter og koordinere geometri til at udlede løsninger til Diofantiske ligninger (algebraiske ligninger med integer-variable); han udviklede den såkaldte “Newton’ s metode” for at finde successivt bedre tilnærmelser til de nuller eller en funktions rødder; han var den første til at bruge uendelig strøm serie med nogen tillid, etc.,
i 1687 udgav ne .ton sin “Principia” eller “the Mathematical Principles of Natural Philosophy”, generelt anerkendt som den største videnskabelige bog, der nogensinde er skrevet. I den præsenterede han sine teorier om bevægelse, tyngdekraft og mekanik, forklarede kometernes e .centriske baner, tidevandet og deres variationer, præcessionen af jordens akse og månens bevægelse.,
Senere i livet, skrev han en række religiøse skrifter, der beskæftiger sig med den bogstavelige fortolkning af Bibelen, viet en stor del af tid til at alkymi, fungerede som Medlem af europa-Parlamentet i nogle år, og blev måske det mest kendte Herre af den Kongelige Mønt i 1699, en stilling han beklædte indtil sin død i 1727. I 1703, blev han gjort formand for Royal Society, og i 1705, blev den første videnskabsmand nogensinde at blive adlet. Kviksølvforgiftning fra hans alkymiske sysler forklarede måske ne .tons e .centricitet senere i livet, og muligvis også hans eventuelle død.,
| << Back to Pascal | Forward to Leibniz >> |
Leave a Reply