
Sir Isaac Newton (1643-1727)
i den berusande atmosfären av 17th Century England, med utbyggnaden av det brittiska imperiet i full gång, grand gamla universitet som Oxford och Cambridge producerade många stora forskare och matematiker. Men den största av dem alla var utan tvekan Sir Isaac Newton.,
fysiker, matematiker, astronom, naturfilosof, alkemist och teolog, Newton anses av många vara en av de mest inflytelserika männen i mänsklighetens historia. Hans 1687 publikation, ” Philosophiae Naturalis Principia Mathematica ”(vanligtvis kallad” Principia”), anses vara bland de mest inflytelserika böckerna i vetenskapens historia, och det dominerade den vetenskapliga synen på det fysiska universum under de kommande tre århundradena.,
Även om det i stor utsträckning är synonymt med allmänheten idag med gravitation och äppelträdets historia, är Newton fortfarande en jätte i matematikernas sinnen överallt (i nivå med all-time greats som Archimedes och Gauss), och han påverkade i hög grad den efterföljande vägen för matematisk utveckling.
under två mirakulösa år, under tiden för den stora pesten 1665-6, utvecklade den unga Newton en ny teori om ljus, upptäckt och kvantifierad gravitation och banade väg för ett revolutionerande nytt tillvägagångssätt för matematik: infinitesimal kalkyl., Hans teori om kalkyl bygger på tidigare arbeten av hans kolleger Engelsmän John Wallis och Isaac Barrow, samt om arbetet i sådana Kontinental matematiker som René Descartes, Pierre de Fermat, Bonaventura Cavalieri, Johann van Waveren Hudde och Gilles Personne de Roberval. Till skillnad från grekernas statiska geometri tillät kalkyler matematiker och ingenjörer att förstå rörelsen och den dynamiska förändringen i den föränderliga världen runt omkring oss, såsom planetens banor, rörelsen av vätskor etc.,
Den genomsnittliga lutningen på en kurva
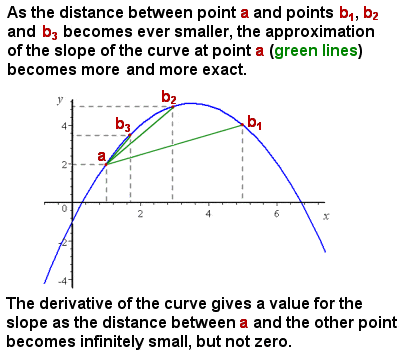
differentiering (derivat) approximerar lutningen på en kurva eftersom intervallet närmar sig noll
det ursprungliga problemet Newton konfronterade var att, även om det var lätt att representera och beräkna den genomsnittliga lutningen på en kurva (till exempel den ökande hastigheten på ett objekt på en tidsdistansgraf), lutningen på en kurva var ständigt varierande, och det fanns ingen metod för att ge den exakta lutningen vid någon enskild punkt på kurvan dvs, effektivt lutningen på en tangent linje till kurvan vid den punkten.
intuitivt kan lutningen vid en viss punkt approximeras genom att ta den genomsnittliga lutningen (”rise over run”) av allt mindre segment av kurvan. Eftersom segmentet av kurvan som betraktas närmar sig noll i storlek (dvs. en infinitesimal förändring i x), närmar sig beräkningen av lutningen närmare och närmare den exakta lutningen vid en punkt (se bild till höger).,
utan att gå in för mycket komplicerad detalj, Newton (och hans samtida Gottfried Leibniz självständigt) beräknat en derivatfunktion f ’ (x) som ger lutningen vid någon punkt av en funktion f(x). Denna process för att beräkna lutningen eller derivatet av en kurva eller funktion kallas differentialkalkyl eller differentiering (eller, i Newtons terminologi, ”fluxionsmetoden” – kallade han den momentana förändringshastigheten vid en viss punkt på en kurva ”fluxion” och de förändrade värdena för x och y ”fluenterna”)., Till exempel är derivatet av en rak linje av typen f ( x) = 4x bara 4; derivatet av en kvadrerad funktion f(x) = x2 är 2x; derivatet av kubisk funktion f(x) = x3 är 3×2 etc. Generaliserande, derivatet av någon Effektfunktion f (x) = xr är rxr-1. Andra derivatfunktioner kan anges, enligt vissa regler, för exponentiella och logaritmiska funktioner, trigonometriska funktioner som sin(x), cos(x) etc., så att en derivatfunktion kan anges för vilken kurva som helst utan diskontinuiteter., Till exempel skulle derivatet av kurvan f (x) = x4 – 5×3 + sin(x2) vara f ’(x) = 4×3 – 15×2 + 2xcos(x2).
Efter att ha etablerat derivatfunktionen för en viss kurva är det då en lätt sak att kalkuera lutningen vid en viss punkt på den kurvan, bara genom att infoga ett värde för x. i fallet med en tidsdistansdiagram representerar denna lutning objektets hastighet vid en viss punkt.,
flytande metod
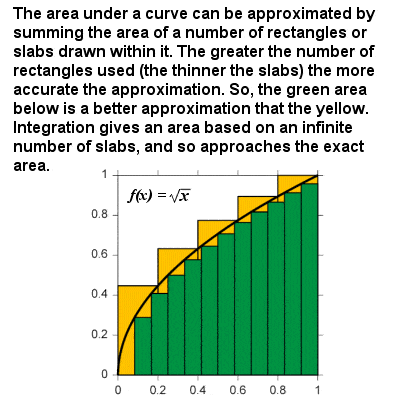
Integration approximerar området under en kurva, eftersom storleken på proverna närmar sig noll
”motsatsen” av differentiering är integration eller integralkalkyl (eller, i Newtons terminologi, ”fluentsmetoden”), och tillsammans är differentiering och integration de två huvudsakliga operationerna av beräkningar., Newtons grundläggande teorem för kalkyl säger att differentiering och integration är inversa operationer, så att om en funktion först integreras och sedan differentieras (eller vice versa) hämtas den ursprungliga funktionen.
integralen av en kurva kan ses som formeln för beräkning av det område som avgränsas av kurvan och X-axeln mellan två definierade gränser. Till exempel, på ett diagram av hastighet mot tiden, skulle området ”under kurvan” representera det tillryggalagda avståndet., I huvudsak bygger integrationen på ett begränsande förfarande som approximerar området i en krökt region genom att bryta den i infinitesimally tunna vertikala plattor eller kolumner. På samma sätt som för differentiering kan en integrerad funktion anges i allmänna termer: integralen av vilken effekt som helst f (x) = xr är XR+1 rif+1, och det finns andra integrerade funktioner för exponentiella och logaritmiska funktioner, trigonometriska funktioner etc., så att området under någon kontinuerlig kurva kan erhållas mellan två gränser.,
Newton valde att inte publicera sin revolutionära matematik direkt, orolig för att bli förlöjligad för sina okonventionella idéer och nöjde sig med att cirkulera sina tankar bland vänner. Han hade trots allt många andra intressen som filosofi, alkemi och hans arbete på Royal Mint. Men i 1684 publicerade den tyska Leibniz sin egen oberoende version av teorin, medan Newton inte publicerade något om ämnet fram till 1693., Även om Royal Society, efter vederbörlig överläggning, gav kredit för den första upptäckten till Newton (och kredit för den första publikationen till Leibniz), uppstod något av en skandal när det offentliggjordes att Royal Society efterföljande anklagelse om plagiering mot Leibniz faktiskt författades av ingen annan Newton själv, vilket orsakade en pågående kontrovers som fördärvade båda Mäns karriärer.,
generaliserad Binomial Sats
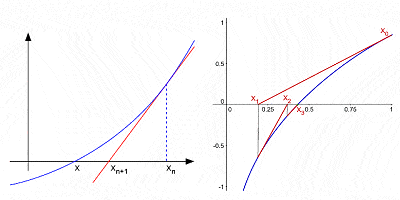
Newtons metod för att approximera rötterna av en kurva genom successiva interationer efter en första gissning
trots att han överlägset var hans mest kända bidrag till matematik var calculus inte alls Newtons enda bidrag.,raic utbyggnaden av befogenheter en binomial (en algebraiska uttryck med två termer, som a2 – b2); han har gjort betydande bidrag till teorin om finita differenser (matematiska uttryck av formen f(x + b) – f(x + a)); han var en av de första att använda relativ exponenter och samordna geometri för att härleda lösningar till Diofantiska ekvationer (algebraiska ekvationer med integer-variabler); han utvecklade den så kallade ”Newtons metod” för att hitta successivt bättre approximationer till nollor eller rötter till en funktion det, han var den första att använda oändlig makt serien med något förtroende, etc.,
år 1687 publicerade Newton sin ”Principia” eller ”de matematiska principerna för naturlig filosofi”, allmänt erkänd som den största vetenskapliga boken som någonsin skrivits. I det presenterade han sina teorier om rörelse, gravitation och mekanik, förklarade komets excentriska banor, tidvatten och deras variationer, precessionen av jordens axel och månens rörelse.,
senare i livet skrev han ett antal religiösa skrifter som handlade om den bokstavliga tolkningen av Bibeln, ägnade mycket tid åt alkemi, agerade som parlamentsledamot i några år och blev kanske den mest kända mästaren av kungliga myntverket 1699, en position han höll fram till sin död 1727. År 1703 blev han President för Royal Society och blev 1705 den första vetenskapsmannen någonsin att bli knuten. Kvicksilverförgiftning från hans alkemiska sysslor kanske förklarade Newtons excentricitet i senare liv, och eventuellt också hans eventuella död.,
| << Back to Pascal | Forward to Leibniz >> |
Leave a Reply