
Statisticile sunt aranjament de teste statistice care analiștii folosi pentru a face inferențe de la datele oferite. Aceste teste ne permit să luăm decizii pe baza modelului observat din date. Există o gamă largăde teste statistice. Alegerea testului statistic utilizat se bazează pe structura datelor, distribuția datelor și tipul de variabilă.,Există mai multe tipuri diferite de teste în statistici,cum ar fi t-test,Z-test, testul chi-pătrat ,testul anova, testul binomial, un test median de probă etc.
alegerea unui test statistic –
testele parametrice sunt utilizate dacă datele sunt distribuite în mod normal .Un test statistic parametric face o presupunere despre parametrii populației și distribuțiile din care provin datele. Aceste tipuri de teste includ teste t, teste z și teste anova, care presupun că datele provin din distribuția normală.,
Z-test – un z-test este un test statistic utilizat pentru a determina dacă două mijloace de populație sunt diferite atunci când variațiile sunt cunoscute și dimensiunea eșantionului este mare. În testul z se compară media populației.Parametrii utilizați sunt media populației și deviația standard a populației. Testul Z este utilizat pentru a valida o ipoteză conform căreia eșantionul extras aparține aceleiași populații.,
Ho: media eșantionului este aceeași cu media populației (ipoteza nulă)
Ha: media eșantionului nu este aceeași cu media populației(ipoteza alternativă)
z = (x — μ) / (σ/√n),
unde , x=media eșantionului, u=media populației, σ / √n = deviația standard a populației.
dacă valoarea z este mai mică decât valoarea critică acceptați ipoteza nulă, altfel respingeți ipoteza nulă.
T-test-în t-test se compară media celor două probe date. Un test t este utilizat atunci când parametrii populației (deviația medie și standard) nu sunt cunoscuți.,T-Test asociat-teste pentru diferența dintre două variabile din aceeași populație( scor pre – și post test). De exemplu – într-un program de formare scorul de performanță al stagiarului înainte și după finalizarea programului.Independent T-test-independent t-test, care este, de asemenea, numit două probă t-test sau student t-test, este un test statistic care determină dacă există o diferență semnificativă statistic între mijloacele în două grupuri care nu au legătură.De exemplu-Compararea băieților și fetelor într-o populație.,
un eșantion t-test – media unui singur grup este comparată cu o medie dată. De exemplu-pentru a verifica creșterea și scăderea vânzărilor dacă sunt date vânzările medii.
t = (x1 — x2) / (σ / √N1 + σ/√N2),
unde x1 și x2 sunt medii ale eșantionului 1 și, respectiv, ale eșantionului 2.testul ANOVA-analiza varianței (ANOVA) este o tehnică statistică care este utilizată pentru a verifica dacă mijloacele a două sau mai multe grupuri sunt semnificativ diferite unele de altele. ANOVA verifică impactul unuia sau mai multor factori prin compararea mijloacelor diferitelor eșantioane., Dacă vom folosi un t-test în loc de test ANOVA nu va fi de încredere ca numărul de probe sunt mai mult de două și va da eroare în rezultatul.
ipoteza testată în ANOVA este
Ho: toate perechile de probe sunt aceleași, adică., toate eșantion de mijloace sunt egale
Ha: Cel puțin o pereche de probe este semnificativ diferit
În testul anova vom calcula valoarea F și se compară cu valoarea critică
F= ((SSE1 — SSE2)/m)/ SSE2/n-k, în cazul în care
SSE = suma reziduală a pătratelor
m = numărul de restricții
k = numărul variabilelor independente
nonparametric test statistic – Non parametric teste sunt utilizate atunci când datele nu sunt normal distribuite. Testele non parametrice includ testul chi-pătrat.testul chi-pătrat( testul χ2)-testul chi-pătrat este utilizat pentru a compara două variabile categorice., Calcularea valorii statistice Chi-pătrat și compararea acesteia cu o valoare critică din distribuția Chi-pătrat permite evaluarea dacă frecvența observată este semnificativ diferită de frecvența așteptată.ipoteza testată pentru chi-pătrat este –
Ho: variabila x și variabila y sunt independente
Ha: variabila x și variabila y nu sunt independente.,
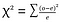
where o=observed , e=expected.
Leave a Reply