
Sir Isaac Newton (1643-1727)
În atmosfera impetuos de al 17-Lea în Anglia, odată cu extinderea imperiului Britanic în plină desfășurare, grand vechi universități ca Oxford și Cambridge au fost producătoare de mulți mari oameni de știință și matematicieni. Dar cel mai mare dintre ei a fost, fără îndoială, Sir Isaac Newton.,fizician, matematician, astronom, filozof natural, alchimist și teolog, Newton este considerat de mulți drept unul dintre cei mai influenți oameni din istoria omenirii. Lui 1687 publicare, „Philosophiae Naturalis Principia Mathematica” (de obicei, numit pur și simplu „Principia”), este considerat a fi printre cele mai influente cărți din istoria științei, și a dominat științifică a universului fizic pentru următoarele trei secole.,deși în mare parte sinonim în mintea publicului larg astăzi cu gravitatea și povestea mărului, Newton rămâne un gigant în mintea matematicienilor de pretutindeni (la egalitate cu cei mai buni din toate timpurile precum Arhimede și Gauss) și a influențat foarte mult calea ulterioară a dezvoltării matematice.de-a lungul a doi ani miraculoși, în timpul Marii ciume din 1665-6, tânărul Newton a dezvoltat o nouă teorie a luminii, a descoperit și cuantificat gravitația și a pionierat o nouă abordare revoluționară a matematicii: calculul infinitezimal., Teoria de calcul a construit pe munca mai devreme, de către colegii săi Englezi John Wallis și Isaac Barrow, precum și pe activitatea de astfel de Continental matematicieni ca René Descartes, Pierre de Fermat, Bonaventura Cavalieri, Johann van Waveren Hudde și Gilles Personne de Roberval. Spre deosebire de geometria statică a grecilor, calculul a permis matematicienilor și inginerilor să înțeleagă mișcarea și schimbarea dinamică în lumea în schimbare din jurul nostru, cum ar fi orbitele planetelor, mișcarea fluidelor etc.,
Panta Medie de o Curba
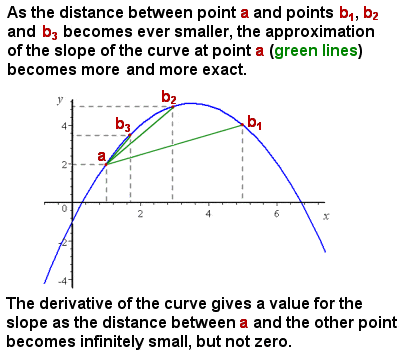
Diferențiere (derivate) aproximează panta unei curbe ca intervalul se apropie de zero
problema initiala Newton a fost confruntarea a fost că, deși a fost destul de ușor de a reprezenta și de a calcula panta medie de o curbă (de exemplu, viteza de creștere a unui obiect pe un timp-grafic de la distanta), panta unei curbe a fost în mod constant diferite, și nu a fost nici o metoda de a da exact panta la fiecare punct de pe curba anume, în mod eficient panta unei linii tangente la curba de la acel punct.în mod intuitiv, panta dintr-un anumit punct poate fi aproximată luând panta medie („rise over run”) a segmentelor tot mai mici ale curbei. Pe măsură ce segmentul curbei considerate se apropie de dimensiunea zero (adică o schimbare infinitezimală în x), atunci calculul pantei se apropie din ce în ce mai aproape de panta exactă într-un punct (vezi imaginea din dreapta).,fără a intra în detalii prea complicate, Newton(și contemporanul său Gottfried Leibniz independent) a calculat o funcție derivată f ‘(x) care dă panta în orice punct al unei funcții f (x). Acest proces de calcul panta sau derivate dintr-o curbă sau o funcție se numește calcul diferențial sau diferențiere (sau, în Newton terminologie, „metoda de nobil” – el a numit rata instantanee de schimbare la un anumit punct de pe o curbă „fluxion”, și de a schimba valorile x și y „fluents”)., De exemplu, derivatul unei linii drepte de tipul f (x) = 4X este doar 4; derivatul unei funcții pătrate f(x) = x2 este 2x; derivatul funcției cubice f(x) = x3 este 3×2 etc. Generalizând, derivata oricărei funcții de putere f(x) = xr este rxr-1. Alte funcții derivate pot fi declarate, conform anumitor reguli, pentru funcții exponențiale și logaritmice, Funcții trigonometrice precum sin(x), cos(x), etc, astfel încât o funcție derivată poate fi declarată pentru orice curbă fără discontinuități., De exemplu, derivata curbei f(x) = x4 – 5×3 + sin(x2) ar fi f ‘(x) = 4×3 – 15×2 + 2xcos(x2).
după ce a stabilit funcția derivat pentru o anumită curbă, atunci este o chestiune ușoară să calcuate panta la un anumit punct de pe curba, doar prin introducerea unei valori pentru x. În caz de timp-grafic de la distanta, de exemplu, această pantă reprezintă viteza de obiect la un anumit punct.,
Metoda de Fluents
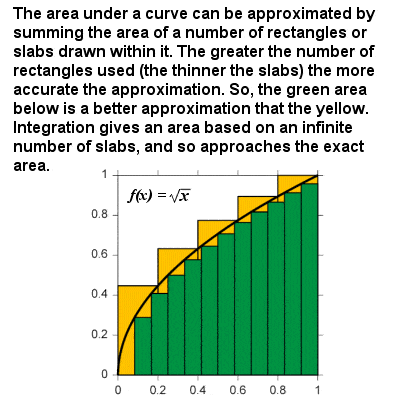
Integrarea aproximează aria de sub curba ca dimensiunea probelor se apropie de zero
„vizavi” de diferențiere este de integrare sau de calcul integral (sau, în Newton terminologie, „metoda de fluents”), și împreună diferențiere și integrare sunt două operațiuni principale de calcul., Teorema fundamentală a lui Newton de calcul afirmă că diferențierea și integrarea sunt operații inverse, astfel încât, dacă o funcție este mai întâi integrată și apoi diferențiată (sau invers), funcția inițială este recuperată.integrala unei curbe poate fi considerată ca formula pentru calcularea ariei delimitate de curbă și axa x între două limite definite. De exemplu, pe un grafic al vitezei față de timp, zona „sub curbă” ar reprezenta distanța parcursă., În esență, integrarea se bazează pe o procedură de limitare care aproximează zona unei regiuni curbilinii prin ruperea acesteia în plăci sau coloane verticale infinitezimale subțiri. În același mod ca și pentru diferențiere, o funcție integrală poate fi declarată în termeni generali: integrala oricărei puteri f(x) = xr este xr+1⁄r+1 și există alte funcții integrale pentru funcții exponențiale și logaritmice, Funcții trigonometrice etc., astfel încât zona de sub orice curbă continuă să poată fi obținută între oricare două limite.,Newton a ales să nu-și publice imediat matematica revoluționară, îngrijorat de faptul că este ridiculizat pentru ideile sale neconvenționale și mulțumit să-și circule gândurile printre prieteni. La urma urmei, el a avut multe alte interese, cum ar fi filosofia, alchimia și munca sa la Monetăria Regală. Cu toate acestea, în 1684, germanul Leibniz și-a publicat propria versiune independentă a teoriei, în timp ce Newton nu a publicat nimic pe această temă până în 1693., Deși Societatea Regală, după deliberare, a dat credit pentru prima descoperire a lui Newton (și de credit pentru prima publicație la Leibniz), ceva de un scandal a apărut atunci când a fost făcut public faptul că Societatea Regală ulterioare acuzația de plagiat împotriva Leibniz a fost de fapt scris de nimeni altul Newton însuși, provocând o continuă controversă care a marcat carierele de bărbați.,
Generalizată Teorema Binomului
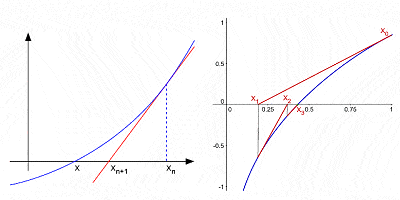
Metoda lui Newton pentru aproximarea rădăcinilor unei curbe succesive de interations după o presupunere inițială
în Ciuda fiind de departe cel mai cunoscut contribuție la matematică, calcul fost în nici un caz lui Newton doar contribuție.,raic extinderea competențelor de un binom (o expresie algebrică cu doi termeni, cum ar fi a2 – b2); el a făcut substanțiale contribuții la teoria diferențelor finite (expresii matematice de forma f(x + b) – f(x + a)); a fost unul dintre primii care au folosit exponenții fracționare și coordona geometrie pentru a obține soluții la Diophantine ecuațiilor (algebrice, ecuații cu întreg-doar variabile); el a dezvoltat așa-numita „metoda lui Newton” pentru găsirea succesiv mai bune aproximări a zerouri sau rădăcini ale unei funcții; el a fost primul care a folosit puterea infinita serie cu orice încredere; etc.,în 1687, Newton a publicat „Principia” sau „principiile matematice ale filozofiei naturale”, recunoscută în general ca cea mai mare carte științifică scrisă vreodată. În el, el și-a prezentat teoriile despre mișcare, gravitație și mecanică, a explicat orbitele excentrice ale cometelor, mareele și variațiile lor, precesiunea axei Pământului și mișcarea Lunii.,
mai Târziu în viață, el a scris o serie de broșuri religioase de-a face cu interpretarea literală a Bibliei, și-a dedicat o mare parte din timp a alchimiei, a acționat ca Membru al Parlamentului timp de câțiva ani, și a devenit, probabil, cel mai cunoscut Maestru al Royal Mint în 1699, o poziție pe care a deținut-o până la moartea sa în anul 1727. În 1703, a fost făcut președinte al Societății Regale și, în 1705, a devenit primul om de știință care a fost cavaler vreodată. Otrăvirea cu mercur din preocupările sale alchimice a explicat probabil excentricitatea lui Newton în viața ulterioară și, eventual, și eventuala sa moarte.,
| << Back to Pascal | Forward to Leibniz >> |
Leave a Reply