ISAAC NEWTON: Math & Calculus

Sir Isaac Newton (1643-1727)

in de onstuimige sfeer van het 17e-eeuwse Engeland, met de expansie van het Britse Rijk in volle gang, produceerden grote oude universiteiten als Oxford en Cambridge vele grote wetenschappers en wiskundigen. Maar de grootste van Allen was ongetwijfeld Sir Isaac Newton.,fysicus, wiskundige, astronoom, natuurfilosoof, alchemist en theoloog Newton wordt door velen beschouwd als een van de meest invloedrijke mannen in de menselijke geschiedenis. Zijn publicatie uit 1687, de “Philosophiae Naturalis Principia Mathematica “(meestal simpelweg de” Principia ” genoemd), wordt beschouwd als een van de meest invloedrijke boeken in de geschiedenis van de wetenschap, en het domineerde de wetenschappelijke kijk op het fysisch universum voor de komende drie eeuwen.,hoewel Newton in de hoofden van het grote publiek tegenwoordig grotendeels synoniem is met zwaartekracht en het verhaal van de appelboom, blijft Newton een reus in de hoofden van wiskundigen overal (op een lijn met de all-time grootheden zoals Archimedes en Gauss), en hij beïnvloedde het verdere pad van wiskundige ontwikkeling sterk.gedurende twee wonderbaarlijke jaren, tijdens de tijd van de grote plaag van 1665-6, ontwikkelde de jonge Newton een nieuwe theorie van licht, ontdekte en gekwantificeerde zwaartekracht, en pionierde een revolutionaire nieuwe benadering van de wiskunde: infinitesimale calculus., Zijn rekentheorie bouwde voort op eerder werk van zijn landgenoten John Wallis en Isaac Barrow, evenals op werk van continentale wiskundigen als René Descartes, Pierre de Fermat, Bonaventura Cavalieri, Johann Van Waveren Hudde en Gilles Personne de Roberval. In tegenstelling tot de statische meetkunde van de Grieken, calculus toegestaan wiskundigen en ingenieurs om zin te maken van de beweging en dynamische verandering in de veranderende wereld om ons heen, zoals de banen van planeten, de beweging van vloeistoffen, enz.,

De Gemiddelde Helling van een Kromme

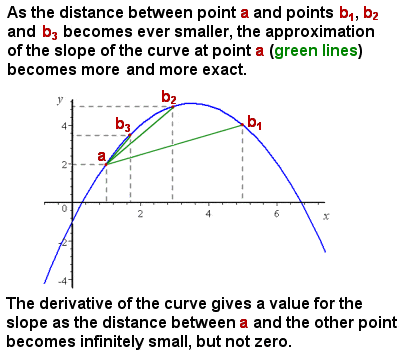
Differentiatie (afgeleide) benadert de helling van een kromme als het interval nul nadert

Het eerste probleem Newton was confronterend was dat, hoewel het was gemakkelijk te vertegenwoordigen en het berekenen van de gemiddelde helling van een kromme (bijvoorbeeld de toenemende snelheid van een object op een tijd-afstand grafiek), de helling van een kromme is een constant veranderende, en er was geen methode om de exacte helling in een punt op de curve d.w.z., effectief de helling van een raaklijn aan de curve op dat punt.

intuïtief kan de helling op een bepaald punt worden benaderd door de gemiddelde helling (“rise over run”) van steeds kleinere segmenten van de curve te nemen. Als het segment van de kromme die wordt beschouwd nul nadert in grootte (dat wil zeggen een infinitesimale verandering in x), dan nadert de berekening van de helling dichter en dichter bij de exacte helling op een punt (zie afbeelding rechts).,

zonder al te ingewikkeld in detail te treden, berekende Newton (en zijn tijdgenoot Gottfried Leibniz onafhankelijk) een afgeleide functie f ‘(x) die de helling geeft op elk punt van een functie f(x). Dit proces van het berekenen van de helling of afgeleide van een kromme of functie wordt differentiaalrekening of differentiatie genoemd (of, in Newton ‘ s terminologie, de “methode van fluxions” – hij noemde de momentane snelheid van verandering op een bepaald punt op een kromme de “fluxion”, en de veranderende waarden van x en y de “fluents”)., Bijvoorbeeld, de afgeleide van een rechte lijn van het type f(x) = 4x is gewoon 4; de afgeleide van een kwadraatfunctie f(x) = x2 is 2x; de afgeleide van derdegraads functie f(x) = x3 is 3×2, enz. Generaliserend, is de afgeleide van om het even welke machtsfunctie f(x) = xr rxr-1. Andere afgeleide functies kunnen volgens bepaalde regels worden vermeld voor exponentiële en logaritmische functies, trigonometrische functies zoals sin(x), cos(x), enz., zodat een afgeleide functie kan worden vermeld voor elke kromme zonder discontinuïteiten., Bijvoorbeeld, de afgeleide van de kromme f (x) = x4 – 5×3 + sin(x2) zou zijn f ‘(x) = 4×3 – 15×2 + 2xcos(x2).

nadat de afgeleide functie voor een bepaalde kromme is vastgesteld, is het eenvoudig om de helling op een bepaald punt op die kromme te calculeren, gewoon door een waarde voor x in te voegen. in het geval van een tijdafstandgrafiek, bijvoorbeeld, vertegenwoordigt deze helling de snelheid van het object op een bepaald punt.,

methode van vloeibaarheid

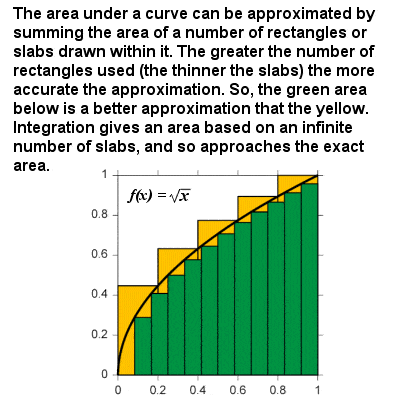
integratie benadert het gebied onder een curve als de grootte van de monsters nul nadert

het “tegenovergestelde” van differentiatie is integratie of Integrale calculus (of, in Newton ‘ s terminologie, de “methode van vloeibaarheid”), en samen differentiatie en integratie zijn de twee belangrijkste bewerkingen van calculus., De fundamentele stelling van Newton van de Calculus stelt dat differentiatie en integratie inverse operaties zijn, zodat, als een functie eerst wordt geïntegreerd en vervolgens gedifferentieerd (of vice versa), de oorspronkelijke functie wordt opgehaald.

De integraal van een kromme kan worden beschouwd als de formule voor het berekenen van het gebied dat wordt begrensd door de kromme en de x-as tussen twee gedefinieerde grenzen. Bijvoorbeeld, op een grafiek van snelheid tegen tijd, zou het gebied “onder de curve” de afgelegde afstand vertegenwoordigen., In wezen is integratie gebaseerd op een beperkingsprocedure die het oppervlak van een kromlijnig gebied benadert door het te breken in infinitesimaal dunne verticale platen of kolommen. Op dezelfde manier als voor differentiatie, kan een integraal functie in algemene termen worden gesteld: de integraal van elke macht f (x) = xr is xr+1⁄r+1, en er zijn andere integraal functies voor exponentiële en logaritmische functies, trigonometrische functies, enz., zodat het gebied onder elke continue kromme kan worden verkregen tussen elke twee grenzen.,Newton koos ervoor om zijn revolutionaire wiskunde niet meteen te publiceren, omdat hij zich zorgen maakte dat hij belachelijk zou worden gemaakt voor zijn onconventionele ideeën en tevreden was met het verspreiden van zijn gedachten onder vrienden. Hij had immers vele andere interesses, zoals filosofie, alchemie en zijn werk bij de Koninklijke Munt. Echter, in 1684 publiceerde de Duitse Leibniz zijn eigen onafhankelijke versie van de theorie, terwijl Newton niets over het onderwerp publiceerde tot 1693., Hoewel de Royal Society, na rijp beraad, de eer voor de eerste ontdekking aan Newton gaf (en de eer voor de eerste publicatie aan Leibniz), ontstond er iets van een schandaal toen het openbaar werd gemaakt dat de daaropvolgende beschuldiging van plagiaat tegen Leibniz eigenlijk geschreven was door niemand anders Newton zelf, wat een voortdurende controverse veroorzaakte die de carrières van beide mannen ontsierde.,

veralgemeende Binomiale stelling

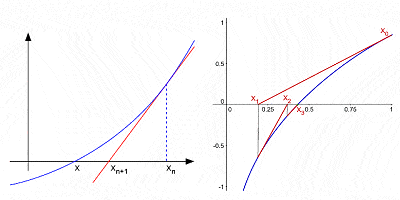
Newton ‘ s methode voor het benaderen van de wortels van een kromme door opeenvolgende interaties na een eerste schatting

ondanks het feit dat hij veruit zijn bekendste bijdrage aan de wiskunde was, was calculus geenszins de enige bijdrage van Newton.,raic uitbreiding van de bevoegdheden van een binomiaal (een algebraïsche uitdrukking met twee termen, zoals de a2 – b2); hij leverde belangrijke bijdragen aan de theorie van de eindige verschillen (wiskundige uitdrukkingen van de vorm f(x + b) – f(x + a)); hij was een van de eerste gebruik van de fractionele exponenten en coördineren van geometrie voor het afleiden van oplossingen voor Diophantine vergelijkingen (algebraïsche vergelijkingen met geheel getal, alleen-variabelen); hij ontwikkelde de zogenaamde “Newton’ s methode” voor het vinden van achtereenvolgens betere benaderingen voor de nullen of wortels van een functie; hij was de eerste die oneindige macht serie met enig vertrouwen; enz.,in 1687 publiceerde Newton zijn ” Principia “of” the Mathematical Principles of Natural Philosophy”, algemeen erkend als het grootste wetenschappelijke boek ooit geschreven. Daarin presenteerde hij zijn theorieën over beweging, zwaartekracht en mechanica, legde hij de excentrische banen van kometen, de getijden en hun variaties, de precessie van de aardas en de beweging van de maan uit.,later in zijn leven schreef hij een aantal religieuze traktaten over de letterlijke interpretatie van de Bijbel, wijdde hij veel tijd aan de alchemie, trad hij enkele jaren op als parlementslid en werd hij misschien wel de bekendste meester van de Koninklijke Munt in 1699, een positie die hij bekleedde tot zijn dood in 1727. In 1703 werd hij President van de Royal Society en in 1705 werd hij de eerste wetenschapper die ooit geridderd werd. Kwikvergiftiging door zijn alchemistische bezigheden verklaart misschien Newton ‘ s excentriciteit in het latere leven, en mogelijk ook zijn uiteindelijke dood.,