
Le statistiche sono la disposizione di test statistici che gli analisti utilizzare per fare inferenza dai dati forniti. Questi test ci consentono di prendere decisioni sulla base del modello osservato dai dati. Esiste un’ampia gamma di test statistici. La scelta di quale test statistico utilizzare si basa sulla struttura dei dati, sulla distribuzione dei dati e sul tipo di variabile.,Esistono molti tipi diversi di test nelle statistiche come t-test,Z-test,test chi-quadrato, test anova ,test binomiale, test mediano di un campione ecc.
Scelta di un test statistico-
I test parametrici vengono utilizzati se i dati sono normalmente distribuiti .Un test statistico parametrico fa un’ipotesi sui parametri della popolazione e sulle distribuzioni da cui provengono i dati. Questi tipi di test includono test t, test z e test anova, che presuppongono che i dati provengano dalla distribuzione normale.,
Z-test – A z-test è un test statistico utilizzato per determinare se due mezzi di popolazione sono diversi quando le varianze sono note e la dimensione del campione è grande. Nel test z viene confrontata la media della popolazione.I parametri utilizzati sono la media della popolazione e la deviazione standard della popolazione. Z-test viene utilizzato per convalidare un’ipotesi che il campione estratto appartiene alla stessa popolazione.,
Ho: media del Campione è la stessa come la media della popolazione(ipotesi nulla)
Ha: la media del Campione non è uguale alla media della popolazione(ipotesi Alternativa)
z = (x — µ) / (s / √n),
dove x=media del campione, u=media della popolazione, s / √n = deviazione standard della popolazione.
Se il valore z è inferiore al valore critico accetta ipotesi nulla altrimenti rifiuta ipotesi nulla.
T-test – In t-test vengono confrontate le medie dei due campioni dati. Un test t viene utilizzato quando i parametri di popolazione (media e deviazione standard) non sono noti.,
Accoppiato T-Test-Test per la differenza tra due variabili della stessa popolazione (punteggio pre e post test). Per esempio – In un programma di formazione punteggio delle prestazioni del tirocinante prima e dopo il completamento del programma.
T-test indipendente-Il t-test indipendente che è anche chiamato t-test a due campioni o t-test dello studente, è un test statistico che determina se esiste una differenza statisticamente significativa tra i mezzi in due gruppi non correlati.Ad esempio, confrontando ragazzi e ragazze in una popolazione.,
Un campione t-test-La media di un singolo gruppo viene confrontata con una data media. Ad esempio, per verificare l’aumento e la diminuzione delle vendite se viene fornita la media delle vendite.
t = (x1 — x2) / (σ / √n1 + σ / √n2),
dove x1 e x2 sono rispettivamente la media del campione 1 e del campione 2.
ANOVA Test – Analisi della varianza (ANOVA) è una tecnica statistica che viene utilizzata per verificare se i mezzi di due o più gruppi sono significativamente diversi l’uno dall’altro. ANOVA controlla l’impatto di uno o più fattori confrontando i mezzi di diversi campioni., Se usiamo un t-test invece di ANOVA test non sarà affidabile in quanto il numero di campioni è più di due e darà errore nel risultato.
L’ipotesi testata in ANOVA è
Ho: Tutte le coppie di campioni sono uguali, cioè, tutti i mezzi di campione sono uguali
Ha: almeno un paio di campioni è significativamente diverso
anova test abbiamo calcolare il valore di F e confrontarlo con il valore critico
F= ((SSE1 — SSE2)/m)/ SSE2/n-k, dove
SSE = somma dei quadrati dei residui
m = numero di restrizioni
k = numero di variabili indipendenti
Non parametrici test statistico Non parametrico test vengono utilizzati quando i dati non sono distribuiti normalmente. I test non parametrici includono il test chi-quadrato.
Test Chi-quadrato (χ2 test)-test chi-quadrato viene utilizzato per confrontare due variabili categoriali., Calcolare il valore statistico del Chi-Quadrato e confrontarlo con un valore critico della distribuzione del Chi-Quadrato consente di valutare se la frequenza osservata è significativamente diversa dalla frequenza prevista.
L’ipotesi testata per il chi-quadrato è-
Ho: La variabile x e la Variabile y sono indipendenti
Ha: la variabile x e la Variabile y non sono indipendenti.,
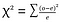
where o=observed , e=expected.
Leave a Reply