
Sir Isaac Newton (1643-1727)
In der berauschenden Atmosphäre des 17. Aber der größte von allen war zweifellos Sir Isaac Newton.,
Der Physiker, Mathematiker, Astronom, Naturphilosoph, Alchemist und Theologe Newton wird von vielen als einer der einflussreichsten Männer der Menschheitsgeschichte angesehen. Seine Veröffentlichung von 1687, die „Philosophiae Naturalis Principia Mathematica „(gewöhnlich einfach“ Principia “ genannt), gilt als eines der einflussreichsten Bücher in der Geschichte der Wissenschaft und dominierte die wissenschaftliche Sicht auf das physische Universum für die nächsten drei Jahrhunderte.,
Obwohl Newton in den Köpfen der breiten Öffentlichkeit heute weitgehend gleichbedeutend mit der Schwerkraft und der Geschichte des Apfelbaums ist, bleibt er überall ein Riese in den Köpfen der Mathematiker (auf Augenhöhe mit den Allzeitgrößen wie Archimedes und Gauss), und er hat den späteren Weg der mathematischen Entwicklung stark beeinflusst.
Über zwei wundersame Jahre, während der Zeit der Großen Pest von 1665-6, entwickelte der junge Newton eine neue Theorie des Lichts, entdeckte und quantifizierte die Gravitation und war Pionier einer revolutionären neuen Herangehensweise an die Mathematik: Infinitesimalrechnung., Seine Theorie der Kalkül basiert auf früheren Arbeiten seiner Engländer John Wallis und Isaac Barrow sowie auf Arbeiten von kontinentalen Mathematikern wie René Descartes,Pierre de Fermat, Bonaventura Cavalieri, Johann van Waveren Hudde und Gilles Personne de Roberval. Im Gegensatz zur statischen Geometrie der Griechen erlaubte das Kalkül Mathematikern und Ingenieuren, die Bewegung und den dynamischen Wandel in der sich verändernden Welt um uns herum, wie die Umlaufbahnen von Planeten, die Bewegung von Flüssigkeiten usw., zu verstehen.,
Die durchschnittliche Steigung einer Kurve
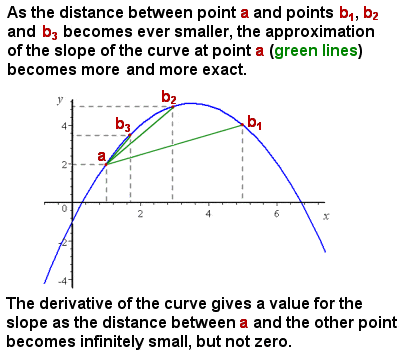
Die Differenzierung (Ableitung) approximiert die Steigung einer Kurve, wenn sich das Intervall Null nähert
Das anfängliche Problem, mit dem Newton konfrontiert war, bestand darin, dass, obwohl es leicht genug war, die durchschnittliche Steigung einer Kurve darzustellen und zu berechnen (z. B. die zunehmende Geschwindigkeit eines Objekts in einem Zeitabstandsdiagramm), die Steigung einer Kurve es gab keine Methode, um die genaue Steigung an einem einzelnen Punkt der Kurve anzugeben., effektiv die Steigung einer Tangente zur Kurve an diesem Punkt.
Intuitiv kann die Steigung an einem bestimmten Punkt angenähert werden, indem die durchschnittliche Steigung („rise over run“) immer kleinerer Kurvensegmente zugrunde gelegt wird. Wenn sich das Segment der betrachteten Kurve der Größe Null nähert (dh eine infinitesimale Änderung in x), nähert sich die Berechnung der Steigung immer näher der genauen Steigung an einem Punkt (siehe Bild rechts).,
Ohne auf zu viele komplizierte Details einzugehen, berechneten Newton (und sein Zeitgenosse Gottfried Leibniz unabhängig voneinander) eine Ableitungsfunktion f ‘(x), die die Steigung an jedem Punkt einer Funktion f(x) angibt. Dieser Prozess der Berechnung der Steigung oder Ableitung einer Kurve oder Funktion wird Differentialrechnung oder Differenzierung genannt (oder in Newtons Terminologie die „Methode der Fluxionen“ – er nannte die momentane Änderungsrate an einem bestimmten Punkt auf einer Kurve die „Fluxion“ und die sich ändernden Werte von x und y die „Fluents“)., Zum Beispiel ist die Ableitung einer geraden Linie vom Typ f(x) = 4x nur 4; die Ableitung einer quadratischen Funktion f(x) = x2 ist 2x; die Ableitung der kubischen Funktion f(x) = x3 ist 3×2 usw. Verallgemeinernd ist die Ableitung einer beliebigen Potenzfunktion f(x) = xr rxr-1. Andere abgeleitete Funktionen können nach bestimmten Regeln für exponentielle und logarithmische Funktionen, trigonometrische Funktionen wie sin(x), cos(x) usw. angegeben werden, so dass eine abgeleitete Funktion für jede Kurve ohne Diskontinuitäten angegeben werden kann., Für Beispiel, die Ableitung der Kurve f(x) = x4 – 5×3 + sin(x2) wäre f ‚(x) = 4×3 – 15×2 + 2xcos(x2).
Nachdem die Ableitungsfunktion für eine bestimmte Kurve festgelegt wurde, ist es leicht, die Steigung an einem bestimmten Punkt dieser Kurve zu berechnen, indem einfach ein Wert für x eingefügt wird. ,
Methode der fließenden
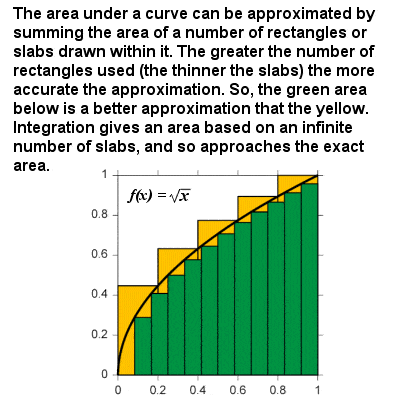
Die Integration nähert sich der Fläche unter einer Kurve, wenn sich die Größe der Stichproben Null nähert
Das“ Gegenteil „der Differenzierung ist Integration oder Integralrechnung (oder in Newtons Terminologie die“ Methode der fließenden“), und zusammen sind Differenzierung und Integration die beiden Hauptoperationen der Berechnung., Newtons grundlegender Berechnungssatz besagt, dass Differenzierung und Integration inverse Operationen sind, so dass, wenn eine Funktion zuerst integriert und dann differenziert wird (oder umgekehrt), die ursprüngliche Funktion abgerufen wird.
Das Integral einer Kurve kann als Formel zur Berechnung der von der Kurve und der x-Achse begrenzten Fläche zwischen zwei definierten Grenzen betrachtet werden. In einem Diagramm der Geschwindigkeit gegen die Zeit würde beispielsweise die Fläche „unter der Kurve“ die zurückgelegte Strecke darstellen., Im Wesentlichen basiert die Integration auf einem begrenzenden Verfahren, das die Fläche eines krummlinigen Bereichs annähert, indem es in unendlich dünne vertikale Platten oder Säulen zerlegt wird. In der gleichen Weise wie für die Differenzierung kann eine Integralfunktion allgemein angegeben werden: Das Integral einer beliebigen Potenz f(x) = xr ist xr+1⁄r+1, und es gibt andere Integralfunktionen für exponentielle und logarithmische Funktionen, trigonometrische Funktionen usw., so dass die Fläche unter einer kontinuierlichen Kurve zwischen zwei beliebigen Grenzen erhalten werden kann.,
Newton entschied sich, seine revolutionäre Mathematik nicht sofort zu veröffentlichen, machte sich Sorgen, wegen seiner unkonventionellen Ideen lächerlich gemacht zu werden, und begnügte sich damit, seine Gedanken unter Freunden zu verbreiten. Schließlich hatte er viele andere Interessen wie Philosophie, Alchemie und seine Arbeit an der Royal Mint. 1684 veröffentlichte der deutsche Leibniz jedoch seine eigene unabhängige Version der Theorie, während Newton bis 1693 nichts zu diesem Thema veröffentlichte., Obwohl die Royal Society Newton nach reiflicher Überlegung die erste Entdeckung (und Leibniz die erste Veröffentlichung) zuerkannte, entstand ein Skandal, als bekannt wurde, dass der spätere Plagiatsvorwurf der Royal Society gegen Leibniz tatsächlich von keinem anderen Newton selbst verfasst wurde, was zu einer anhaltenden Kontroverse führte, die die Karriere beider Männer beeinträchtigte.,
Verallgemeinerter Binomialsatz
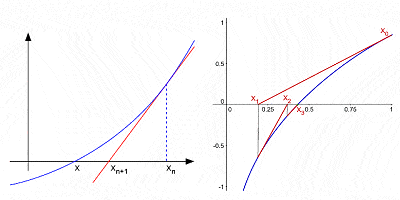
Newtons Methode zur Annäherung an die Wurzeln einer Kurve durch aufeinanderfolgende Wechselwirkungen nach einer anfänglichen Vermutung
Obwohl er mit Abstand sein bekanntester Beitrag zur Mathematik war, war Calculus keineswegs Newtons einziger Beitrag.,raic Erweiterung der Kräfte eines Binoms (ein algebraischer Ausdruck mit zwei Begriffen, wie a2 – b2); er leistete wesentliche Beiträge zur Theorie der endlichen Unterschiede (mathematische Ausdrücke der Form f(x + b) – f(x + a)); er war einer der ersten, der fraktionierte Exponenten und Koordinatengeometrie verwendete, um Lösungen für diophantische Gleichungen abzuleiten (algebraische Gleichungen mit nur ganzzahligen Variablen); er entwickelte die sogenannte „Newtonsche Methode“, um nacheinander bessere Annäherungen an die Nullen oder Wurzeln einer Funktion zu finden.; er war der erste, der Infinite Power Series mit jedem Vertrauen verwendete; usw.,
Im Jahr 1687 veröffentlichte Newton seine „Principia“ oder „Die mathematischen Prinzipien der Naturphilosophie“, allgemein anerkannt als das größte wissenschaftliche Buch, das jemals geschrieben wurde. Darin präsentierte er seine Bewegungstheorien, Schwerkraft und Mechanik, erklärte die exzentrischen Umlaufbahnen von Kometen, die Gezeiten und ihre Variationen, die Präzession der Erdachse und die Bewegung des Mondes.,
Später im Leben schrieb er eine Reihe von religiösen Schriften, die sich mit der wörtlichen Auslegung der Bibel befassten, widmete der Alchemie viel Zeit, war einige Jahre Parlamentsabgeordneter und wurde 1699 vielleicht der bekannteste Meister der Königlichen Münzstätte, eine Position, die er bis zu seinem Tod 1727 innehatte. 1703 wurde er Präsident der Royal Society und 1705 der erste Wissenschaftler, der jemals zum Ritter geschlagen wurde. Eine Quecksilbervergiftung durch seine alchemistischen Aktivitäten erklärte vielleicht Newtons Exzentrizität im späteren Leben und möglicherweise auch seinen späteren Tod.,
| << Back to Pascal | Forward to Leibniz >> |
Leave a Reply