
Les statistiques sont à la disposition des tests statistiques que les analystes utiliser pour faire de l’inférence à partir de données. Ces tests nous permettent de prendre des décisions sur la base du modèle observé à partir de données. Il existe une large gamme de tests statistiques. Le choix du test statistique à utiliser dépend de la structure des données, de la distribution des données et du type de variable.,Il existe de nombreux types de tests dans les statistiques comme le test t,le test Z,le test du chi carré, le test anova ,le test binomial, le test médian d’un échantillon, etc.
le Choix d’un test Statistique-
tests Paramétriques sont utilisés si les données sont distribuées normalement .Un test statistique paramétrique fait une hypothèse sur les paramètres de population et les distributions d’où proviennent les données. Ces types de tests comprennent les tests t, les tests z et les tests anova, qui supposent que les données proviennent d’une distribution normale.,
z-test – Un z-test est un test statistique utilisé pour déterminer si deux moyennes de population sont différentes lorsque les variances sont connues et que la taille de l’échantillon est grande. Dans le test Z, la moyenne de la population est comparée.Les paramètres utilisés sont la population moyenne et l’écart type de population. Le test Z est utilisé pour valider une hypothèse selon laquelle l’échantillon prélevé appartient à la même population.,
Ho: moyenne d’Échantillonnage est la même que la moyenne de population(hypothèse Nulle)
Ha: moyenne d’Échantillonnage n’est pas la même que la moyenne de population(autre hypothèse)
z = (x — µ) / (σ / √n),
où x=moyenne d’échantillon, u=moyenne de population, σ / √n = écart-type de population.
Si la valeur de z est inférieure à la valeur critique accepter l’hypothèse nulle de rejeter l’hypothèse nulle.
T-test t-test de la moyenne des deux échantillons sont comparés. Un test t est utilisé lorsque les paramètres de population (moyenne et écart type) ne sont pas connus.,
Test t apparié-Tests pour la différence entre deux variables de la même population( score avant et après le test). Par exemple – dans un programme de formation score de performance du stagiaire avant et après la fin du programme.
Test t indépendant-le test T indépendant, également appelé test T à deux échantillons ou test T de student, est un test statistique qui détermine s’il existe une différence statistiquement significative entre les moyennes dans deux groupes non apparentés.Par exemple-comparer les garçons et les filles dans une population.,
un échantillon T-test – la moyenne d’un seul groupe est comparée à une moyenne donnée. Par exemple-pour vérifier l’augmentation et la diminution des ventes si les ventes moyennes sont données.
t = (x1 — x2) / (σ / √n1 + σ / √n2),
où x1 et x2 sont des moyennes de l’exemple 1 et l’exemple 2, respectivement.
Test D’ANOVA – L’analyse de la variance (ANOVA) est une technique statistique utilisée pour vérifier si les moyennes de deux groupes ou plus sont significativement différentes les unes des autres. ANOVA vérifie l’impact d’un ou plusieurs facteurs en comparant les moyennes de différents échantillons., Si nous utilisons un test t au lieu d’un test ANOVA, il ne sera pas fiable car le nombre d’échantillons est supérieur à deux et cela donnera une erreur dans le résultat.
l’hypothèse testée dans ANOVA est
Ho: toutes les paires d’échantillons sont identiques, c’est-à-dire, toutes les moyennes d’échantillons sont égales
Ha: au moins une paire d’échantillons est significativement différente
dans le test anova, nous calculons la valeur F et la comparons à la valeur critique
F= ((SSE1 — SSE2)/m)/ SSE2/n-k, où
SSE = somme résiduelle des carrés
M = nombre de restrictions
k = nombre de test – des tests non paramétriques sont utilisés lorsque les données ne sont pas normalement distribuées. Les tests non paramétriques incluent le test du chi carré.
Test du chi-carré( test χ2)- le test du chi-carré est utilisé pour comparer deux variables catégorielles., Le calcul de la valeur statistique du Chi carré et sa comparaison avec une valeur critique de la distribution du Chi carré permettent d’évaluer si la fréquence observée est significativement différente de la fréquence attendue.
L’hypothèse en cours de test de chi-carré est-
Ho: la Variable x et la Variable y sont indépendantes
Ha: la Variable x et la Variable y ne sont pas indépendantes.,
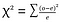
where o=observed , e=expected.
Leave a Reply