ISAAC NEWTON: Matematiikka & Calculus

Sir Isaac Newton (1643-1727)

Vuonna huumaava tunnelma 17-Luvulla Englannissa, laajentaminen Brittiläisen imperiumin täydessä vauhdissa, grand old yliopistoja kuten Oxford ja Cambridge olivat tuottavat monet suuret tiedemiehet ja matemaatikot. Mutta suurin niistä kaikista oli epäilemättä Sir Isaac Newton.,

Fyysikko, matemaatikko, tähtitieteilijä, luonnollinen filosofi, alkemisti ja teologi Newton on monien mielestä olla yksi vaikutusvaltaisimmista miesten ihmiskunnan historiassa. Hänen 1687 julkaisu, ”Philosophiae Naturalis Principia Mathematica” (yleensä kutsutaan yksinkertaisesti ”Principia”), on pidetään yhtenä vaikutusvaltaisimmista kirjoja tieteen historiassa, ja se hallitsi tieteellinen näkemys fyysisen maailmankaikkeuden seuraavan kolmen vuosisadan ajan.,

Vaikka pitkälti synonyymi mielissä yleisölle tänään painovoima ja tarina omenapuu, Newton on edelleen jättiläinen matemaatikkojen mielissä kaikkialla (par kaikkien aikojen parhaimmisto kuten Arkhimedes ja Gauss), ja hän vaikutti suuresti myöhemmin polku matemaattista kehitystä.

Yli kaksi vuotta ihmeellinen, aikana Suuri Rutto 1665-6, nuori Newton kehitti uuden teorian valossa, löysi ja määrälliset gravitaatio, ja edelläkävijä vallankumouksellinen uusi lähestymistapa matematiikkaan: äärettömän pieni calculus., Hänen teoria, calculus rakennettu aiemmin työ hänen kaveri Englantilaiset John Wallis ja Isaac Barrow, sekä työtä kuten Continental matemaatikot kuten René Descartes, Pierre de Fermat, Bonaventura Cavalieri, Johann van Waveren Hudde ja Gilles Personne de Roberval. Toisin kuin staattinen geometria Kreikkalaiset, calculus saa matemaatikot ja insinöörit järkeä liike ja dynaaminen muutos muuttuvassa maailmassa ympärillämme, kuten kiertoradat planeettoja, liike nesteitä, jne.,

Keskimääräinen Kaltevuus Käyrän

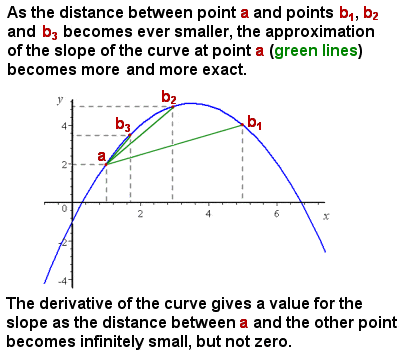
Eriyttäminen (johdannaissopimukset) muistuttavat kaltevuus käyrä aikaväli lähestyy nollaa

alkuperäiseen ongelmaan Newton oli vastakkain oli, että, vaikka se oli helppoa edustaa ja laske keskimääräinen kaltevuus käyrän (esimerkiksi kasvava nopeus objektin aika-matka-kuvaaja), kaltevuus käyrän oli jatkuvasti vaihteleva, ja siellä ei menetelmä antaa tarkan rinne tahansa yksittäisen käyrän eli, tehokkaasti kaltevuus tangenttiviivan käyrä, että kohta.

intuitiivisesti tietyn pisteen kaltevuutta voidaan approksimoida ottamalla käyrän yhä pienempien segmenttien keskimääräinen kaltevuus (”rise over run”). Koska segmentti käyrä pidetään lähestyy nollaa koko (eli äärettömän pieni muutos x), niin laskettaessa rinne lähestyy lähemmäs ja lähemmäs tarkka kulmakerroin pisteessä (ks. kuva oikealla).,

– ei kuitenkaan liian monimutkainen yksityiskohtaisesti, Newton (ja hänen aikalaisensa Gottfried Leibniz itsenäisesti) lasketaan johdannainen funktio f ’(x), joka antaa rinteessä missään vaiheessa funktio f(x). Tämän prosessin, jossa lasketaan rinteessä tai johdannainen käyrä tai toiminto on nimeltään differential calculus tai eriyttäminen (tai Newtonin terminologiaa, ”menetelmä fluxions” – hän kutsui hetkellinen muutosnopeus tietyn pisteen käyrä ”fluxion”, ja muuttuvat arvot x ja y ”fluents”)., Esimerkiksi johdannainen suora tyyppi f(x) = 4x on vain 4; johdannainen neliöllinen funktio f(x) = x2 on 2x; johdannainen cubic funktio f(x) = x3 on 3×2, jne. Yleistäen minkä tahansa tehofunktion F(x) = xr derivaatta on rxr-1. Muut johdannaissopimukset toiminnot voidaan todeta, tiettyjen sääntöjen mukaan, sillä eksponentti-ja logaritmifunktiot, trigonometriset funktiot kuten sin(x), cos(x), jne, niin, että johdannainen toiminto voi olla todettu tahansa käyrä ilman epäjatkuvuuskohtia., Esimerkiksi derivaatta käyrän f(x) = x4 – 5×3 + sin(x2) olisi f ’(x) = 4×3 – 15×2 + 2xcos(x2).

todettuaan johdannainen toiminto tietyn käyrä, se on niin helppo asia calcuate rinne milloin tahansa erityisesti kohta, että käyrä, vain lisäämällä arvo x. Jos aika-matka kuvaaja, esimerkiksi, tämä rinne edustaa kohteen nopeus tietyssä pisteessä.,

Menetelmä Fluents

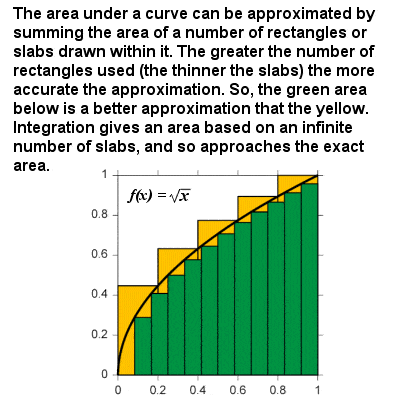
Integraatio on lähellä ala-käyrä kuin koko näytteitä lähestyy nollaa

”vastapäätä” eriyttäminen on integraatio tai integral calculus (tai Newtonin terminologiaa, ”menetelmä fluents”), ja yhdessä eriyttäminen ja integrointi ovat kaksi tärkeintä toiminta-ja integraalilaskenta., Newtonin Perusvapauksien Lause Calculus todetaan, että eriyttäminen ja integrointi ovat käänteinen toiminta, niin, että jos funktio on ensin integroitu ja sitten eriytetty (tai päinvastoin), alkuperäinen toiminto on haettu.

integraali, käyrä voidaan ajatella laskentakaava alueen, jota rajoittavat käyrän ja x-akselin välillä kaksi määriteltyjä rajoja. Esimerkiksi kuvaaja nopeuden aikaa vastaan, alue ”käyrän” edustaisi kuljetun matkan., Pohjimmiltaan, integraatio perustuu rajoittava menettely, joka vastaa alueen kaareva alue rikkomalla sen äärettömän ohut pystysuora laatat tai sarakkeita. Samalla tavalla kuin eriyttäminen, olennainen toiminto voidaan todeta yleisesti: olennainen mitään valtaa f(x) = xr on xr+1⁄r+1, ja siellä on muut olennainen toiminnot, eksponentiaalinen ja logaritmifunktiot, trigonometriset toiminnot, jne, niin, että alue missään jatkuva käyrä voidaan saada tahansa kahden rajoja.,

Newton valitsi ei julkaista hänen vallankumouksellinen matematiikan heti, huolissaan naurunalaiseksi hänen epäsovinnaisia ideoita, ja tyytyi kiertävä hänen ajatuksia ystävien kesken. Loppujen lopuksi hänellä oli monia muita etuja, kuten filosofia, alkemia ja hänen työnsä Royal Mint. Saksalainen Leibniz julkaisi kuitenkin vuonna 1684 oman riippumattoman versionsa teoriasta, kun taas Newton ei julkaissut aiheesta mitään ennen vuotta 1693., Vaikka Royal Society, jälkeen, koska käsittely, antoi luottoa ensimmäinen löytö Newton (ja luotto ensimmäinen julkaisu Leibniz), pieni skandaali syntyi, kun se oli julkistettu, että Royal Society on myöhemmin syytös plagioinnista vastaan Leibniz oli itse asiassa kirjoittanut kukaan muu Newton itse, mikä aiheuttaa jatkuvaa kiistaa, joka varjostivat uraa sekä miehille.,

Yleisen Binomisen Lause

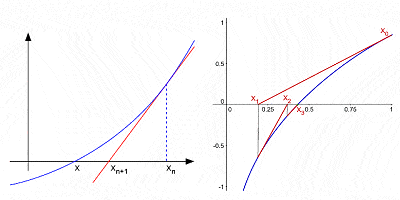
Newtonin Menetelmä lähentää juuret käyrän peräkkäisten interations jälkeen alkuperäisen arvaus

Huolimatta siitä, että ylivoimaisesti hänen tunnetuin panoksen matematiikka, calculus, ei suinkaan Newtonin ainoa panos.,raic laajentaminen toimivalta binomial (algebrallinen lauseke, jossa on kaksi termejä, kuten a2 – b2); hän teki merkittäviä osuuksia teorian finite eroja (matemaattisia lausekkeita muotoa f(x + b) – f(x + a)); hän oli yksi ensimmäisistä käyttää murto-eksponentit ja koordinoida geometria perustuvat ratkaisut Diophantine yhtälöt (algebrallinen yhtälöiden kanssa integer-vain muuttujat); hän kehitti ns ”Newtonin menetelmä” löytää toisensa paremmin likiarvoilla nollia tai juuret toiminto; hän oli ensimmäinen, joka käyttää ääretön voima-sarjan kanssa mitään luottamusta, jne.,

Vuonna 1687, Newton julkaisi teoksensa ”Principia” tai ”Matemaattinen Periaatteet Natural Philosophy”, yleisesti tunnustettu suurin tieteellinen kirja koskaan kirjoitettu. Siinä hän esitti teoriansa liikkeen, painovoiman ja mekaniikan, selitti eksentrinen kiertoradat, comets, vuorovesi ja niiden muunnelmia, prekessiota Maapallon akselin ja liikkeitä Kuun.,

Myöhemmin elämässä, hän kirjoitti useita uskonnollisia kirjasia, jotka käsittelevät kirjaimellinen Raamatun tulkinta, omistettu paljon aikaa alkemia toimi euroopan Parlamentin Jäsen joitakin vuosia, ja tuli ehkä parhaat-tunnettu Mestari Royal Mint vuonna 1699, kantaa hänen hallussaan kuolemaansa asti vuonna 1727. Vuonna 1703 hänestä tehtiin Royal Societyn puheenjohtaja, ja vuonna 1705 hänestä tuli ensimmäinen tiedemies, joka on koskaan aateloitu. Elohopeamyrkytys hänen alchemical harrastukset ehkä selitti Newtonin eksentrisyys myöhemmässä elämässä, ja mahdollisesti myös hänen lopullinen kuolema.,